|
por Alberto Borrás Gabarró Marzo 1998 del Sitio Web Isis
La Geometría
El significado originario del término Geometría, como su prefijo Geo indica, se refería al estudio de las medidas de la Tierra.
Poco después, pasó a designar la parte de las Matemáticas que conocemos actualmente. Muchos recordaron unos manoseados sólidos de madera que nos ilusionaban al final de la EGB, ya que eran algo tangible.
Entre ellos, se encontraban los cinco poliedros regulares:
No se nos explicó que ya se hallan descritos por Platón, y por ello se llaman los cinco poliedros platónicos.
Sólo hay estos cinco, número sagrado Pitagórico, y ninguno más que con todas sus caras formadas por polígonos regulares y ángulos iguales, puedan inscribirse en una esfera. Recordemos que así como el tetraedro, el cubo y el octaedro, nos parecían más lógicos y fáciles de imaginar, el dodecaedro y el icosaedro, por la ingeniosa forma de distribuir sus caras, nos obsesionaban. A Platón le sucedería lo mismo, ya que hace especial énfasis en esas normas, sobre todo el dodecaedro que contiene el número sagrado Pitagórico 5, en los lados de sus caras, y el también fundamental 12 en su número. Le tenía tanto respeto, que no se atrevía a nombrarlo directamente.
El icosaedro 20 caras y 12 vértices, se puede inscribir en el dodecaedro, un vértice en el centro de cada cara, y el centro de sus caras triangulares en los 20 vértices del dodecaedro. En los cruces de la malla así formada, se pueden apoyar los vértices de los cinco poliedros Platónicos. El dodecaedro, forma la base de la malla de energías sutiles de nuestro planeta.
Es posible que la fascinación que provocan estos dos poliedros proceda del inconsciente colectivo.
En Gran Bretaña se han descubierto colecciones de piedras talladas con las formas de estos sólidos y con surcos que señalaban las aristas, en donde se han hallado restos de cordones de piel. Pueden ser de 1.500 años A.C. o sea, 1.000 años antes de Platón, pero en otros yacimientos las hay que pueden ser de 12.000 años A.C.
Oficialmente se dice, que eran utilizadas como boleadoras para cazar.
Volviendo a la geometría Platónica, en su significado originario, el filósofo Griego, en su diálogo Fedón, no puede ser más claro al describir la estructura de la Tierra, como un dodecaedro esférico.
El Balón Terráqueo
La concepción de la Tierra como un dodecaedro se basa en una premisa relativamente simple: el dodecaedro es el poliedro que más se aproxima a la esfera y el que tiene los ángulos menos salientes, lo que permite curvarlo sin que apenas sufra deformación.
Si fuera el elástico y lo hinchásemos, sus caras curvadas, apoyadas en una esfera, la dividirían en doce partes formadas por pentágonos curvos.
Las líneas que separan estas caras, equivalentes a las aristas del dodecaedro de caras planas, en este caso se prolongan, formando círculos máximos que rodean la esfera.
Estos círculos en su periplo por la esfera, cortan las otras caras, cada una atravesada por cinco de ellos (siempre el cinco), que así queda dividida en diez sectores en forma de triángulos rectángulos.
Para ello es suficiente un total de quince círculos, y no más. Así, entre las 12 caras pentagonales, cada una con 10 triángulos, totalizamos 120 triángulos rectángulos que cubren la superficie de la esfera. Al mismo tiempo, observamos que las líneas que unen los centros de los pentágonos curvos, forman triángulos equiláteros.
Las veinte caras de un icosaedro esférico, cada una de las cuales contiene 6 de los citados triángulos rectángulos.
Es el icosaedro que se intercala al dodecaedro. Estos triángulos rectángulos, son la unidad básica de esta estructura. Así Platón en la segunda parte del diálogo Timeo, describe estos triángulos, en los que se basan todos los poliedros, ya que en sus ángulos sobre la esfera encajan los cinco poliedros.
Ni más ni menos que en la gran pirámide de Cheops, y la razón de que sea así no es nada esotérica. Situada a 29º 58' 51" latitud N y 31º 08' 57" longitud E, se halla en el meridiano que divide la Tierra en dos partes en las que la superficie emergida, los continentes e islas, incluyendo la Antártica, es exactamente igual. El meridiano que pasa por la Gran Pirámide, coincide con un vértice del pentágono Norte. Ello orienta toda la red.
Cinco de sus líneas maestras son meridianos, círculos máximos, que pasan por los vértices de las caras Norte y Sur, y que están alternados.
Estos 120 triángulos rectángulos, unidades básicas de la malla energética terrestre, ya eran conocidos por los antiguos Egipcios, que les llamaban triángulos M. R. (por Amón Ra), por lo que respetaremos esta denominación a lo largo del presente trabajo.
En los textos funerarios Egipcios, este triángulo rectángulo escaleno (con tres lados desiguales) se utilizaba para ilustrar la relación entre el cuerpo físico mortal, denominado KA y los otros tres más sutiles y considerados esencias divinas del hombre, AK, BA y KA, lo que demuestra la enorme importancia que se le daba a esta forma, que se halla también en las caras de la Gran Pirámide, formada por ocho de ellos ensamblados dos a dos.
En esas caras, ambos triángulos no se hallan exactamente en un mismo plano, sino formando un ángulo entrante muy abierto, imperceptible a simple vista, y que sólo puede distinguirse por su iluminación consecutiva y súbita, con pocos segundos de diferencia, en el mismo instante de un equinoccio.
Es el fenómeno que se llama Relámpago.
Hemos repasado la trigonometría esférica, que pilotos y navegantes deberían conocer pero que con los actuales programas informatizados de navegación la mayoría han olvidado.
Así, de acuerdo a nuestros cálculos y para
simplificar, suponiendo la Tierra una esfera perfecta de 40.000
kilómetros de meridiano y Ecuador, la hipotenusa de estos triángulos
curvos M. R. mide 4.153.041 metros, y los catetos 3.524.164 y
2.322.795 metros, lo que suma exactamente 10.000 kilómetros, un
cuarto de
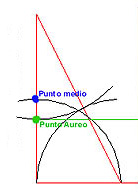
La relación de 1,5172 entre sus catetos curvos, no es significativa. Pero si los proyectamos desde el centro de la Tierra sobre un plano tangente al vértice de su ángulo recto, se forma otro triángulo plano, que nos da exactamente la relación 1,618034... el número áureo Fi, que la pirámide de Cheops contiene entre su Apotéma (la perpendicular entre el lado de la base y el vértice), y la mitad del lado de la base.
Es el número del equilibrio y la belleza, el límite de la serie de Fibonacci, y la razón entre dos partes de un segmento y su suma con la mayor.
Un guarismo que tanto los Griegos, como los constructores de las catedrales Góticas, utilizaron secretamente en sus proporciones arquitectónicas hasta que Leonardo da Vinci lo divulgó.
Ello no sólo demuestra que los antiguos conocían exactamente la trigonometría esférica y sus relaciones con la plana, sino que la red energética del planeta, con el número Fi, es una estructura equilibrada y armonizada con el Cosmos.
Mapas Prehistoricos
Las antiguas cartas marinas, los llamados Portulanos, son trabajosas copias de mapas mucho más antiguos, en los que las formas de los continentes parecen deformadas y las distancias adquieren proporciones absurdas.
Ello se debe a que estos viejos mapas, aparte de un sistema de proyección distinto, se basan en la geometría esférica.
Uno de los más interesantes es el Opicinis de Canestris (1.335) en el que Europa y África están antropomorfizados, representando a un Rey y una Reina; la Península Ibérica como cabeza del Rey, preparándose para besar a la Reina africana. Los discutidos mapas de Piri Reis (1.513) son copias de otros más antiguos que muestran detalladamente el contorno de Sudamérica y de la Antártica, incluso aquellas regiones actualmente cubiertas por el hielo.
También pertenecen a esta cartografía no convencional, pero que demuestra que fueron dibujados por miembros de una antiquísima civilización, dotada de una tecnología similar a la actual.
Algunos de estos mapas, como el de Canestris, incluyen líneas de triángulos M. R., que para los profanos carecen de sentido. Ubican su origen en Alejandría, no en Gizeh.
Esta ciudad, con su biblioteca, fue el centro cultural más importante de Occidente y su puerto mereció un faro calificado como la séptima maravilla del mundo. Por ello no es de extrañar que en estas copias de otras más antiguas, acabara como centro. Lo correcto sería tomar como núcleo un punto en el meridiano de Gizeh llamado Behdet, cerca de la población de Baltim, en el delta del Nilo.
La intersección de este meridiano con el círculo máximo perpendicular, en el mismo centro del lado de dos pentágonos, define 4 triángulos M. R., y forma el centro de un rombo que marcaba la influencia del Imperio Egipcio.
La Red
Estos 15 círculos máximos, 12 pentágonos con 10 triángulos M. R. cada uno, y 62 intersecciones, forman la malla energética que rodea la Tierra, pero dada la extensión de esos, M. R. de más de 4.000.000 de kilómetros cuadrados (dos tercios de Australia), hay pocas oportunidades de que algunos de estos focos y líneas se ubiquen en países.
Se supone que los tres distintos tipos de cruces, los de pentágonos del dodecaedro, con cinco líneas, los triangulares del icosaedro, con tres y los de los rombos, que comprenden 4 M. R., con dos, tienen propiedades distintas, y entre los del mismo tipo, incluso polaridades opuestas, lo que genera corrientes energéticas por las líneas que los unen.
El tipo pentágono con 5 líneas que aparentan los rayos, es el más espectacular, y precisamente uno de ellos, se halla en el cogollo del famoso Triángulo de las Bermudas.
Naturalmente, ello si nos referimos a la red básica, pero si unimos entre sí, otros cruces de círculos máximos distintos, se forma otra tupida red de círculos máximos, que llamaremos secundaria. En ella, entre los ángulos centrales de los pentágonos, como bisectrices, salen otros 5 círculos máximos. Los cruces de tres círculos de los triángulos icosaédricos contienen a su vez nueve más, y los cruces de dos líneas entre cuatro M. R., nada menos 10 círculos máximos más. Asemeja a una tela de araña de círculos que pasan por otros muchos lugares. Precisamente, algunos Leys o Venas de Dragón, termino que se utiliza en Feng Shui, para designar las líneas de fuerza de la Tierra, coinciden con ese trazado que parece secundario, pero puede ser más importante desde el punto de vista energético, que la red básica de 15 círculos, ya que el número de círculos que pasan por un mismo nudo es mayor.
El matemático Buckminster Fuller, pasó la mayor parte de su vida investigando mediante técnicas microfotográficas, una esfera elástica sometida a tensión, como un globo hinchado, encontrando una elaborada y compleja malla de tensiones vectoriales similar a las líneas antes descritas.
Así podríamos seguir con otras redes más finas, hasta el último escalón.
Los capilares de este sistema serían la Cuadrícula de Curry Oblicua, con respecto a los meridianos, y cuyas líneas se encontrarían distanciadas unos 4 metros, con nudos positivos y negativos alternados y la conocida como red de Hartmann, paralela a los meridianos y con una separación de 2 metros de Norte a Sur, y de 2,5 metros de Este a Oeste.
Los Efectos de La Red
Nos hemos limitado a exponer los antecedentes históricos, la geometría, con la descripción de las líneas, las figuras que forma en la superficie terrestre, los distintos tipos de cruces, y los lugares en donde se ubican unos pocos de ellos, que creemos más significativos, y que se detallan en la parte gráfica.
Cuando los antiguos Egipcios se tomaron el trabajo de estudiar y plasmar esta red, sería para algo más tangible que una mera especulación filosófica. Ante todo, los mejores estudios se han efectuado en nudos y líneas secundarias y terciarias que coinciden con los Leys. En 1.977, Paul Devereux emprendió el Proyecto Dragón, a través del cual un equipo multidisciplinar de científicos efectuó gran número mediciones de ultra e infrasonidos, campos magnéticos, ionización y radioactividad. Lo más inexplicable fueron las determinaciones de partículas B, con un scintilómetro.
Estos registros eran totalmente distintos a los de las zonas circundantes, estaban modulados por las fases lunares, la salida y puesta del Sol, y eran mucho más intensos durante los Equinoccios. También se han efectuado estudios en las redes de Curry y Hartmann, para localizar puntos en los que las energías nocivas afectan a la salud de hombres y animales.
Pero de la gran red, aparte de particularidades sobre de los lugares donde se ubican estos nudos, sabemos muy poco.
En los grados más suaves, se limitan a alterar o enloquecer los instrumentos de navegación de los aviones. Pero hay otros fenómenos dignos de ser tenidos en cuenta y que acarrean unas consecuencias mucho menos misteriosas, pero graves.
Es el caso de las CAT, Clear Air Turbulence (Turbulencias en Aire Tranquilo), perturbaciones no detectables por el radar y que han sido causa de cierto número de accidentes de aviación. Un aumento de la gravitación local de sólo un 5 o 10%, no afecta para nada al vuelo de un avión, que en virajes y baches soporta esfuerzos muy superiores, pero si este aumento persiste durante unas horas, atrae el aire de la zona, y lo va acelerando, creando una corriente descendente, que pueden llegar a cientos de kilómetros por hora.
Al no intervenir diferencias de temperaturas que afectan a la densidad del aire, no son detectables por el radar. Si un avión en su ruta, se mete en una de ellas, es arrastrado hacia el suelo a esa velocidad, sin que nada se pueda hacer para evitarlo, sólo mantener su control, esperar a que esta corriente sea estrecha y salir pronto por el otro lado. Con mala suerte puede perder hasta 10.000 pies de altura.
La estructura del avión normalmente aguanta, pero los pasajeros, si no van con el cinturón, son proyectados contra el techo. Esto es lo que pudo ocurrir hace unos quince años durante un vuelo Charter de la compañía Aviaco.
Un DC-8 en ruta desde Santiago de Chile a Paramaribo, repentinamente y sin que apareciera previamente nada sospechoso en la pantalla del radar, experimentó una súbita pérdida de sustentación. Unos cuantos pasajeros que no llevaban el cinturón, salieron despedidos hacia el techo, rompiéndolo.
Una azafata, que tras servir las bebidas a los pasajeros acababa de sentarse en el trasportín, rompió el panel superior con la cabeza. Los carros de bebidas saltaron por los aires, así como las balsas salvavidas, que rompieron sus sujeciones y salieron despedidas de sus alojamientos. Mientras el avión caía, todos se quedaron pegados al techo gritando y pataleando. Cuando salió de esta turbulencia, en la que descendió 3.000 metros de altura, todos cayeron violentamente. La azafata, cuyo asiento se había plegado contra el suelo estuvo varios meses de baja a causa de las heridas sufridas durante este incidente.
El avión seguramente pasó por el cruce de dos líneas situado a unos 330 kilómetros al norte de Manaos, en la misma línea ecuatorial. En el Ecuador se ubican oblicuamente diez nudos de este tipo y actúa como una línea que los conecta energéticamente, potenciando su fuerza. Parece que estos nudos se activan esporádicamente, quizás por causas cósmicas, y en otras ocasiones los aviones pueden haber pasado por el mismo lugar, sin notar nada.
En ese momento los pasajeros se encontraban comiendo en sus asientos. Muchos de ellos que tenían suelto el cinturón para comer con mayor comodidad, salieron despedidos contra los compartimentos portaequipajes.
Como consecuencia del incidente, numerosas personas resultaron heridas y una mujer murió al ser golpeada en la cabeza por una maleta. La situación alcanzó tal gravedad que el piloto se vio obligado a regresar al aeropuerto de la capital Nipona. Precisamente, por la zona que transitaba el aparato se puede apreciar el trazo de dos de los anillos, que convergen en un nudo de cinco a unos 1.000 kilómetros al sur de Tokio.
Algunos han sido cunas de civilizaciones ahora desaparecidas. Muchos lugares sagrados que desde tiempos inmemoriales han albergado santuarios y edificios religiosos en los que se percibe una fuerza insólita, están relacionados con estos puntos o cruces. Por otra parte, estas corrientes energéticas se pueden manipular, desviándolas hacia lugares que precisan de ellas.
Es lo que hacían los hombres prehistóricos con sus Menhires, quizás para aumentar la fertilidad de las tierras, la salud del ganado, influir en el clima, lluvias, u otros fines útiles.
El meridiano energético que pasando por España va del Sahara Argelino al Polo Norte, roza la rivera oeste del lago Ness, otro enclave misterioso. Podemos suponer un ramal energético, quizás artificial, que siguiendo la falla que da origen a este lago, llegue hasta Findhorn. Además, se halla a sólo 80 kilómetros del nudo de dos líneas que puede irradiar una potente corriente secundaria.
En relación a lugares sagrados, una línea secundaria que parte del nudo argelino la bisectriz del ángulo que forma su meridiano con la que pasa por Budapest, es un círculo que da con otro nudo situado al noreste de Siberia, cerca del Mar de Okhotsk, por donde pasa el meridiano que también atraviesa el Monte Fuji. A los Japoneses les choca la ubicación de Montserrat, justamente en esta línea que quizás por ignorancia catalogamos como secundaria.
La predisposición a la apertura de portales interdimensionales en algunos de estos lugares puede estar asociada a la aparición de ovnis, lo que hace que los avistamientos sean más numerosos. Se trata de un hecho perfectamente constatado y tenido en cuenta en las estadística ufológicas.
Esta misma facilidad de conexión con dimensiones situadas en niveles más elevados, según algunos expertos en energía libre, facilitaría el funcionamiento de algunos de estos generadores que captan la energía del punto cero, desde un nivel dimensional superior, y que por ahora funcionan de manera irregular, esporádica, y cuando se trasladan fallan estrepitosamente, lo que impide su utilización práctica.
Para lograr un funcionamiento regular habría que ubicarlos en alguno de estos lugares portal. También podemos pensar, que algunos ovnis utilizan este truco, y por eso se les ve en esos lugares. Ello, junto con las ventajas de tipo humano ya mencionadas, podría llevar en un futuro a una revalorización de estos terrenos donde se ubican estos nudos o líneas.
Todo ello, requiere un conocimiento mucho más profundo de la red, con sus niveles secundarios y terciarios.
Aplicando la geometría esférica, no sería difícil diseñar un programa informático que uniendo todos estos puntos por círculos máximos, nos trazase las líneas de una determinada región del mapa en los tres niveles mencionados, y nos señalase las coordenadas de los puntos de cruce más activos, que habría que comprobar sobre el terreno.
Mapas de Algunos Nudos de La Red
|

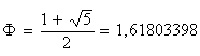
 meridiano, con ángulos de 36, 60 y 90 grados (en los
triángulos esféricos suman más de 180 grados y no se cumple el
teorema de Pitágoras).
meridiano, con ángulos de 36, 60 y 90 grados (en los
triángulos esféricos suman más de 180 grados y no se cumple el
teorema de Pitágoras). 








