"The more extensive a man's knowledge of what has been done, the greater will be his power of knowing what to do."
- Benjamin Disraeli

13. The Ultimate Clue

Every scrap of cycle evidence that we have been able to collect and preserve during the past thirty years can be found in our library at the Foundation. To the best of my knowledge our library contains the most comprehensive collection of cycle material in the world. It is divided into three main sections.

In the Data and Research section we have figures concerning several thousand "time series." A series is a string of figures arranged in some order. A time series is a string of figures arranged in order of time. "Average annual wheat prices in the United States since 1864" is a time series. So is "Average daily temperature at Boston since January 1, 1967." Here you can locate data about earthquakes, tree-ring thicknesses, geological deposits, rainfall, temperature, barometric pressure, auroras, sunspots, planetary positions, wars, animal abundance, disease, prices, production, crops, transportation, trade, etc.

Many of the records go back for hundreds of years, some for a thousand. A few, such as war, sunspot maxima, geological deposits, certain tree-ring measurements, aurora, and earthquakes, extend backward to the pre-Christian era. This section also contains the work papers from any research that we have done on any of these series of figures, either by longhand or by means of the computer.

The second section of the library is where we record the cycle work of others. It contains thousands of articles and clippings and books and reprints of papers in scientific journals alleging cycles of various lengths in the hundreds of phenomena in which such behavior has been observed.

If someone has written that there is a six-year cycle in the abundance of gumbos (or someone has written that there is not), you will find the information here if we have it. Each item in this section is cross-catalogued by branch of science. Thus if a particular paper alleges cycles of a particular length in weather, earthquakes, sunspots, and prices, it is cross-indexed under climatology, geology, astrophysics, and economics. Conversely, if you are interested in geologic cycles you could go to the geologic section of the cross-index file and find the names of all the papers we have in the library in which geologic cycles are recorded and alleged.

The third section of our library is perhaps the most interesting. It is concerned basically with interrelationships - and particularly with interrelationships that might throw light on the cause of cycles.

If someone discovers that snakes are more active when exposed to ultraviolet light, his paper about it is filed here. Then if it is ever discovered that the ultraviolet light reaching the earth has cycles of some particular wavelength, and that some biological phenomena have corresponding cycles, we may be able to get a hint as to the mechanism involved.

If radio weather fluctuates with planetary movements and angular relationships, as it does, maybe other behavior fluctuates this way also. We may not know just what mechanism relates the two phenomena, but we know that there is one. And the mechanism that serves to communicate to the earth the repercussions of whatever it is that happens when the planets bear certain angular relationships to each other may also be the mechanism that conveys faraway cyclic energy forces to earth. It is worth knowing more about.

I could go on and on about all the strange interrelationships that are alleged in the third section of our library.

For instance, here we will learn that when pigeons are released in the neighborhood of radio towers, they cannot orient themselves; that if I stand near you, I will affect the flow of electric current from your hand to your head; and that artificial electric fields will cause dowsers' rods to dip. Some of these allegations need further corroboration, but they are all interesting and suggest that very minor electromagnetic forces may have very important physiological and psychological consequences.

Since a complete catalogue of cycles is as fundamental to cycle study as a list of animals is to the study of zoology, our library also contains thousands of index cards detailing specific cycles. As this collection grew, we were able to begin what has become a never-ending program of comparative cycle study.

Comparative cycle study is "the name of the game" so far as our work is concerned. We compare cycles in all phenomena, searching for similarities and possible relationships among them. For example, the fact that locusts have a seventeen-year cycle is, by itself, of little interest to us. But if apple crops also have a seventeen-year cycle we are intrigued. Is this mere coincidence, or is there something in the atmosphere that affects both locusts and apple trees? If so, what is it? And how does it operate?

If the cycle in one thing were unique and could not be related in length to the length in anything else, it would hold very little interest for us. The openings through which your hair grows change shape in cycles, thus creating wavy hair. But there is no reason even to imagine that a study of these cycles in several people would show any interrelationship. If there were, I would be interested. As there is not, I merely record this behavior as an interesting fact.

However, whenever we discover cycles that have the same length in completely unrelated phenomena, we are put on alert to the possibility that one of the behaviors is the cause of the other, or that both behaviors have a common cause. Of course, with the large numbers of cycles alleged in all sorts of phenomena it would be remarkable if there were not some with the same length merely by chance.

But if cycle lengths were random and completely unrelated, wouldn't you think we would have a fairly even number of cycles of each length, as many fifteen-year cycles as sixteen-year cycles, etc.? And if you discovered, instead, that cycles from completely unrelated phenomena seem to cluster around certain lengths while ignoring others, what would you think?

Consider, for example, the so-called 9.6-year cycle, of which thirty-seven out of many possible examples are listed below.

Is it conceivable that all these various behaviors could have cycles of the same length by chance alone? Or can there be some relationship among most of them?

The Synchrony of Cycles

Now we come to the heart of the matter.

During the past thirty years, as you have seen, we have discovered countless cycles that appeared to fluctuate with amazing regularity. Some of these cycles extend from before the time of Christ, and their rhythm has continued, almost without interruption, through wars, panics, revolutions, depressions, industrial change, and scientific advancement.

We discovered cycles that, after they were distorted, for unknown reasons resumed their old rhythm. We discovered cycles that continued to come true after their discovery. We discovered cycles with the same length and shape in many unrelated phenomena. We discovered that cycles seemed to reach their highs later and later as found nearer and nearer the equator. We discovered that cycles concentrate at particular lengths instead of being evenly distributed among all lengths.

Were all these pieces in our mosaic clues to the possible existence of cycles? Yes.

Were they proof that cycles exist? No. Maybe we were just playing games with numbers. Maybe it was all merely coincidence.

Then we began to look more closely at all the cycles with the same length, and what we discovered convinced not only me but a large body of previously doubting scientists that cycles are a reality.

The ultimate clue finally came to light!

We discovered that all cycles of the same length tend to turn at the same time! They act in synchrony.

Now if it is difficult to find cycles with identical lengths in unrelated phenomena by chance alone, think how much more difficult it is to find cycles with identical lengths that also turn at or about the same calendar time. What amazed us even more was to learn that all cycles of the same length behave this same way. The 5.91-year cycles all turned closely together, the 9.6-year cycles all turned closely together, etc. This was unusually powerful evidence that we were dealing with real and not random behavior.

Sit with me now in our reviewing stand and watch this evidence parade before your eyes in step to silent drums. But while you watch, you must not feel superior, for you too march to those same drums.

You too are in the parade.
 

The Most Significant Evidence
What you are about to see needs little in the way of explanation.

Here are five diagrams, each showing the timing of all available cycles of a particular length for which an ideal turning point has been calculated. The number of years in which each cycle has been observed is also included. No cycles have been excluded because they didn't fall into our ideal pattern. Furthermore, as new cycles are discovered, they almost invariably turn at the same established time of other cycles of similar length.

The dramatic concentration of the timings exhausts the possibility of mere coincidence. The demonstrated synchrony of behavior in all the phenomena that have been timed in each cycle length cannot reasonably be considered chance (see figures 62-66).

If you study the five diagrams you will note that a few phenomena are inverted. These particular cycles have their lows while the others of the same length are having their highs, and vice versa. Thus we have a synchrony of turning points rather than a synchrony of highs and lows. It is the nature of some things to be upside down relative to other things. When your outside temperature is high, the sale of fuel oil is low. When the yield of crops is high, the price of crops is low. When physical production is high, the number of business failures is low.

I suspended personal judgment in regard to cycles for many years. It was only after we discovered that cycles persisted over hundreds and even thousands of years, and after we were able to make comparative cycle studies that showed that substantially all the cycles of any given length turn at about the same time, that I became convinced without any lingering doubts as to the significance of at least some of these behaviors.

It is simply inconceivable that all the observed coincidences could come about as the result of random forces.

The mystery is real!

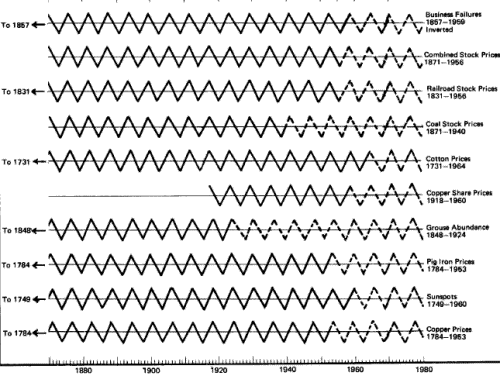
Fig. 62.

The 5.91-Year Cycles on Parade
Diagram to show timing of idealized crests. Note that here and in the following
charts crests come close to the same time. This fact suggests an interrelationship.

 

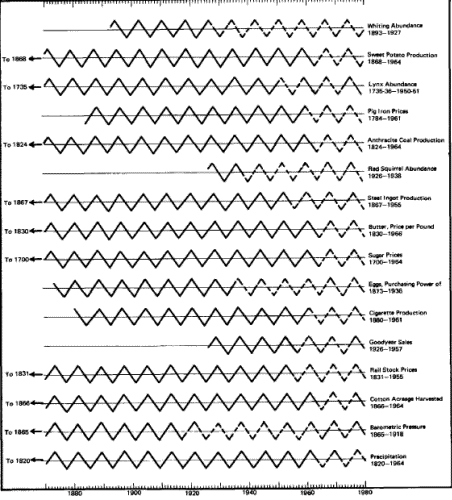
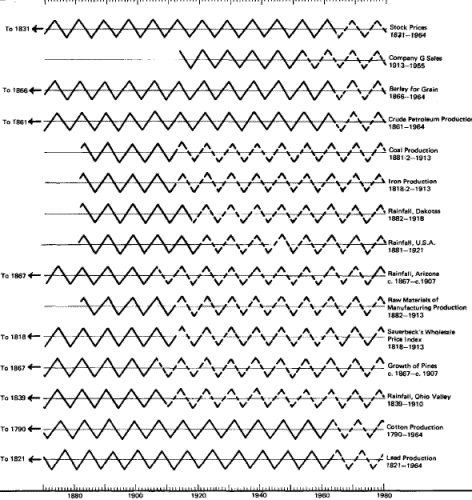
Fig. 63.

The 8-Year Cycles on Parade

 

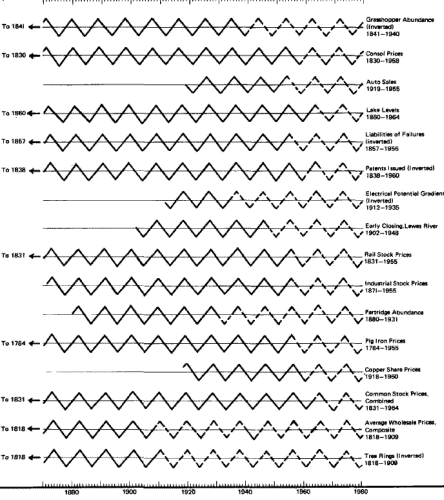
Fig. 64.

The 9.2-Year Cycles on Parade

 

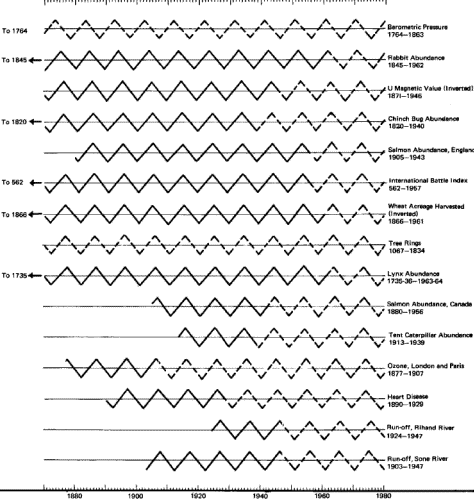
Fig. 65.

The 9.6-Year Cycles on Parade

 

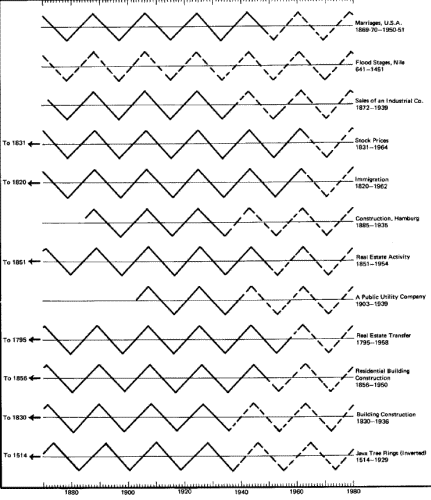
Fig. 66.

The 18.2-Year Cycles on Parade
 

Back to Contents