|
Part I
Some
Definitions
-
The Quantum Mechanical Vacuum: First we need some definitions. We
start by assuming the quantum mechanical vacuum.1 Empty "spacetime"
is filled with an incredibly intense flux of virtual particles. It
is a plenum, not an emptiness. We shall be interested only in the
fantastic flux of virtual photons, for we are discussing
electromagnetics.
-
Energy and Potential: Energy is any ordering, either static or
dynamic, in the virtual particle flux of vacuum. EM energy is any
ordering, either static or dynamic, in the virtual photon flux (VPF)
of vacuum. That is, for a particular kind of "field" energy, we
simply choose the so-called quantum particle of that field, and
consider only that kind of virtual particle flux.
Potential is any ordering, either static or dynamic, in the virtual
particle flux of vacuum. Hey! That's exactly the same definition as
energy. Quite correct. Energy and potential are identically the
same. Neither is presently defined correctly in physics.
Energy is normally defined as "Energy is the capacity to do work."
That's totally false. Energy has the capacity to do work, because
work is correctly defined as the dissipation (disordering;
scattering) of energy (order). The scattering of energy is work. It
is not energy! I.e., energy is not definable as its own scattering!
-
Look at it this way: A man has the capacity to catch fish. That is
true, but it is not a definition, since a definition must in some
sense be an identity. You cannot say that a man is the capacity to
catch fish! That may be a submitted definition, all right, but it is
false. Similarly, energy has the capacity to do work; that is one of
its attributes. But energy IS the ordering in the VPF (we are
referring from now on primarily only to EM).
-
Scalar and Vector Potentials: The scalar potential is any static
(with respect to the external observer) ordering in the VPF of
vacuum. The vector potential is any dynamic (with respect to the
external observer) ordering in the VPF of vacuum. We shall be
interested in the electrostatic scalar potential. So it is a static
ordering -- a stationary template -- in the VPF of vacuum, much as a
whirlpool is a stationary ordering (template, form) in the rushing
flow of a river.
The
Scalar Potential Has An Internal Structure
The Structure of the Scalar Potential:
According to rigorous proofs
by Whittaker2 and Ziolkowski,3 any scalar potential can be
mathematically decomposed into a harmonic series of bidirectional
wave pairs. Figure 1 shows this Whittaker/Ziolkowski (WZ) structure.
In each pair, the forward-time wave is going in one direction, and
its phase conjugate (time-reversed) replica wave is going in the
other. According to the so-called distortion correction theorem4 of
nonlinear phase conjugate optics, this PCR wave must precisely
superpose spatially with its partner wave in the pair. The two waves
are in-phase spatially, but 180 degrees out of phase in time. The
wave is made of photons, and the antiwave (PCR wave) is made of
antiphotons. It follows that, as wave and antiwave pass through each
other, the photons and antiphotons are coupling and uncoupling with
each other, because the antiphoton is a PCR photon, and PCR's
precisely superpose spatially with their partner. A photon or
antiphoton has wave characteristics, because it has a frequency; if
the wave aspects are perfectly ordered and perfectly correlated,
then so are the photon's particle aspects.
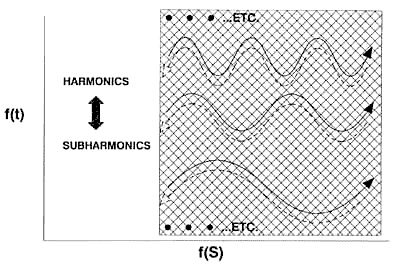
Figure 1a. Internal wave structure of the scalar potential.
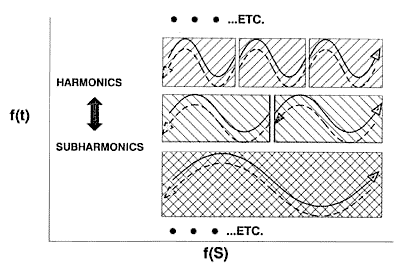
Figure 1b. Internal wave structure of the scalar potential
(end).
A Potential Is An Ordering Across the Universe:
So we have --
astoundingly -- perfect VPF inner ordering infolded in the
electrostatic scalar potential! We also have perfect wave/antiwave
ordering infolded in there. When you collect a simple set of charges
on a small ball or in a region, the scalar EM potential from that
set of charges reaches across the universe. In it you have an
infinite harmonic series of phase-locked time-forward EM waves going
out from the charges to all distant points of the entire universe.
And you have an infinite harmonic series of phase-locked
time-reversed EM waves coming from all points of the universe, back
to the "collected charges" source.
A Potential Is A River of Energy:
The point is, you have established
a mighty, hidden, 2-way river of energy between that collection of
charges and every other point in the universe. There is infinite
energy in each of those infolded waves and antiwaves. But in a
localized region, the energy density in each wave is finite. Since
in finite circuits the potential interacts with a localized set of
mass, we shall be concerned with the local energy density
(joules/coulomb) of the potential.
But forget the conventional myth of visualizing the potential as
pushing a unit charge in from infinity "against the force field" --
there isn't any force field in the vacuum, as is well-known in
quantum mechanics. Also, Newton's third law requires all forces to
occur in pairs -- each pair consisting of a force and its 3rd law
reaction force. From that viewpoint alone, there is no such thing as
an EM forcefield or force field wave in the vacuum. There are just
gradients of the vacuum potential present in the vacuum. In the
vacuum, an EM wave is actually a wave of the phase locked gradients
of the electrostatic scalar potential and of the magnetostatic
scalar potential. And each such gradient wave is simultaneously
accompanied by its phase conjugate gradient wave, because of
Newton's third law.
Newton's third law requires forces to occur in pairs of equal but
antiparallel forces.
Both wave and antiwave co-exist simultaneously in the vacuum EM
wave.5 Therefore it's a stress potential wave, not a force field
wave. It's more like an electromagnetic sound wave,6 and so it is a
longitudinal wave, not a transverse wave. In the EM vacuum wave's
interaction with matter (the so-called "photon" interaction), the
wave normally half interacts with the electron shells of the atom,
giving translation forces, while the anti-wave half interacts with
the atomic nucleus, giving the Newtonian 3rd law reaction (recoil)
forces (waves). The EM wave in vacuum is an electrogravitational
wave.
Energy Is Internally Infinite and Unlimited:
A static potential --
which is identically excess energy -- is internally dynamic and
infinite. Energy is internally infinite and unlimited! But it has a
finite energy density in a local region of spacetime. Since energy
interacts with matter locally, we shall be concerned with the local
energy density (joules per coulomb).
A Principle of Great Importance:
The only way you can have a "chunk"
or finite amount of energy to dissipate in a circuit as work is to
first have a potential's local energy density interact with a local
finite mass collector. The normal interacting mass collector is the
free electrons (the free electron gas) in the circuit. You can have,
e.g., (joules/coulomb x coulomb); (joules/gram x grams); (joules/m3
x m3); etc.
Voltage, Force, Potential Gradients, Loads, and Work:
Now let's look
at circuitry aspects. Conventionally they are a mess. Voltage is
"essentially" defined as the "drop in potential." In other words,
it's the dissipation (disordering) of a "finite amount" of potential
gradient. But the only way you can get a "finite amount" of infinite
energy/potential gradient is by first interacting the potential
gradient's internal, finite, excess energy density with a finite
"collector" mass. E.g., (joules/coulomb available for collection) x
(coulombs collecting) = excess joules collected on the interacting
coulombs, available for dissipation.
So voltage is really the dissipation of a finite collection of
excess EM energy/potential gradient. The dissipation of potential or
of its gradient is not potential! You cannot logically define either
potential or energy as is own dissipation!
We presently use the notion of "voltage" in two completely
contradictory ways in electrical physics. Here's how we got the
confusion: We take a potential gradient (which has a local energy
density), and we "collect" it across some charged masses in a
locality -- usually the free electrons in the free electron gas in
our circuitry. That is, we express the finite energy density of the
potential gradient (before collection onto charges) in the local
region in terms of energy per coulomb. The potential gradient
actually is a change to the ambient potential, and so it contains an
excess energy density (the magnitude may be either positive or
negative). We then collect this potential (actually this potential
density) on a certain number of coulombs, which places tiny little
gradients of potential across (coupled to) each free electron.
The
local excess energy density of the potential gradient multiplied by
the amount of collecting mass gives the amount of excess energy
collected (on the interacting charges/coulombs). On each collecting
particle, that little gradient, together with the coupling particle,
constitutes a tiny force. F is not just equal to ma (non
relativistic case); instead, F º (ma), where (mass x acceleration)
is considered as a unitary, inseparable thing. So that little potentialized electron (that little EM force) moves itself around
the circuit. In the load (scatterer), the little potentialized
electron (the little force) is subjected to jerks and accelerations,
thus radiating energy (shucking its gradient). Since this is done in
all directions in the scatterer (load), that gets rid of the
gradient, reducing the "little force" (potentialized electron) to
zero because the little potential gradient is lost due to radiation.
Collecting And Dissipating Energy
Energy Dissipation and Collection:
Without further ado, we consider
the scalar potential's local energy density in terms of joules per
coulomb. That is, in a specific glob of charges (i.e., in finite
circuits), the amount of energy collected from a potential gradient
onto the finite number of charges receiving/collecting it, is equal
to the number of joules of energy per coulomb that is in the
potential gradient, times the number of coulombs collecting
(receiving) the potential gradient. The current is the activated (potentialized)
coulombs per second that dissipate their potential gradients during
that second. The current multiplied by the time the current flows
gives the activated coulombs that dissipated their activation (potentialization)
during that flow time. Dissipating, activated coulombs multiplied by
the excess energy collected per activated coulomb gives the energy
dissipated (the work or scattering done) in the load.
We define collection as the connection of a potential gradient (a
source) to the charged masses in a circuit element (the element is
called the collector), which for a finite delay time does not allow
its potentialized free electrons to move as current. In the
collector, during this delay time these trapped electrons are
"activated" by potential gradients being coupled to them.
Technically, that delay time in the collector is known as relaxation
time,7 in the case of the free electron gas8 (in a wire or in a
circuit element). A collector then is a circuit element that has a
usable, finite relaxation time. During that relaxation time, the
trapped electrons are potentialized without movement as current;
each collecting/receiving free electron gets a little gradient
across it, but no current yet flows. In other words, during this
finite relaxation time (collection time), we extract potential from
the source, but no current. Thus we extract energy (potential), but
no power (which is voltage x amperage). During the relaxation time,
we extract from the source only a flow of VPF, which is continually
replaced in the source by the vacuum's violent VPF exchange with the
source's bipolarity charges. We do not extract power from the
battery/source during relaxation time, but we extract free energy
density. That free energy density, coupling with a finite quantity
of electrons, gives us a collected finite amount of energy. With
that background, let's start again, and go through this in a useful
"free energy" manner.
The Electron Gas.
We refer to the conventional model of the free
electron gas in a wire.9 Although the electrons in this gas actually
move by quantum mechanical laws and not by classical laws, we shall
simply be dealing with the "on the average" case. So we will speak
of the electrons and their movement in a classical sense, rather
than a quantum mechanical sense, as this will suffice very well for
our purposes.
When one connects a circuit to a source of potential gradient (say,
to a battery), the first thing that happens nearly instantly is that
the potential gradient races onto the coupling wire and heads down
it at almost the speed of light. As it goes onto the wire, this
gradient "couples" to the free electrons in the free electron gas.
However, inside the wire, these electrons can hardly move down the
wire at all; they can only "slip" once in a while, yielding a
"drift" velocity of a fraction of a cm/sec.10 On the surface, things
are just a little bit different. Most of the "current" in a wire, as
is well-known, moves along the surface, giving us the "skin" effect.
[For that reason, many cables are stranded of finer wires, to
provide more skin surface per cm3 of copper, and hence more
current-carrying capability per cm3 of copper.]
So, initially, little gradients of potential appear on and across
each free electron, with a single little
Ñf on each electron, and
coupled to it. The couplet of [Ñf·me], where
me is the mass of the
electron, constitutes a small DEe. [This is rigorous; the
conventional EM notion that an E field exists in the vacuum is
absurd, and it is well-known in QM that no observable force field
exists in the vacuum. As Feynman pointed out, only the potential for
the force field exists in the vacuum,11 not the force field as such.
Or as Lindsay and Margenau pointed out in their Foundations of
Physics, one does not have an observable
force except when observable mass is present.12]. We have stated it
even stronger: Not only is F = ma, but F º ma (nonrelativistic
case).13 Since no observable mass exists in vacuum, then no
observable F exists there either.
Force,
Coupled Gradients, and Electron Translation
Electrons Coupled to a Potential Gradient Move Themselves.
The point
is, when activated by a "coupled potential gradient," the activated
electron moves itself until it loses its activation (its coupled
potential gradient).
Let me say that again, in a little more detail. Forget the standard
notion that a force field such as the E-field causes electrons to
move. Also forget the notion that the E-field is given by E = -Ñf.
In foundations of physics, those equations are known to be incorrect
for the vacuum. EM force fields are known (in QM foundations theory)
to be effects, existing only in and on the charged particles, and
not existing separately at all,14 or in the vacuum at all.15 Instead
of E = -Ñf, in the vacuum the correct equation would be something
like this: PE = -Ñf. In this case, we have correctly stated that the
potential gradient PE provides the potential for producing an
antiparallel E-field in and on a coupling/collecting charged mass,
and the magnitude and direction of that potential gradient will be
given by -Ñf, if and only if a charged mass particle is first
introduced so that it couples to PE.
At any rate, the activated/potentialized electron moves itself. The
reason is that it constitutes a force. Force º (mass x acceleration)
(non relativistic case). So the potentialized/activated electron is
continuously accelerating. However, it is prevented from easily
moving down the wire directly. To begin to do that, it essentially
has to first move to the outer skin of the copper conductor.
The Collector:
We now consider a circuit element that we called a
collector. (It could be a special coil made of special material, a
capacitor with doped plates rather than simple conducting plates, or
any one of a number of things). The objective is for the collector
to be made of special material so that it has a free electron gas
whose electrons are momentarily not free to move as current (they
continue to move violently around microscopically, but essentially
with zero net macroscopic translation) for a finite delay
(relaxation) time, while they are settling themselves upon the
surface and preparing to move as current. Let's call the electrons NNTE (no net translation electrons) during that finite delay
(relaxation time). During that "no-current" delay time, the NNTE
electrons become potentialized/activated by the potential gradient
impressed across the collector. So at the end of the NNT time, the
NNTE electrons are potentialized, and each is of the form [Ñf·me].
The
Secret of Free Energy
Two Circuits/Two Cycles: We are going to use two circuits and two
cycles, as shown in Figure 2:
Nondissipative components are
shown by dotted lines. Dissipative components are
shown by solid lines.
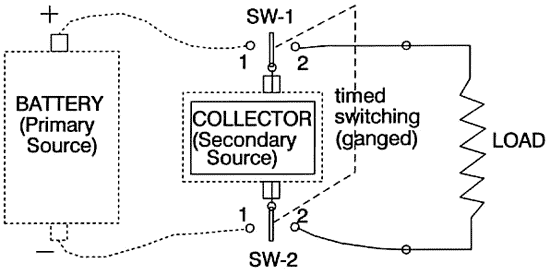
Figure 2. The secret of extracting and using free energy.
(1) We shall connect a
collector to a primary source of potential (to a battery) during
the short time that current does not yet flow, but potential
does. (In other words, during the relaxation time of the
collector, we allow the VPF to flow onto the NNTE electrons of
the collector and potentialize (activate) them, but do not yet
allow the electrons themselves to flow as current, but only to
move transversely in the wiring and collector.) This is cycle
one of a 2-cycle process: This is collection of a specific
amount of current-free potential gradient -- power-free energy
-- off the potential-source (the battery) onto a collector.
During the collection cycle/time, current does not and must not
flow (we are discussing the ideal case). We are freely "charging
up" the collector as a secondary battery/source.
(2) At the end of the collection (potentialization/activation)
time/cycle in circuit one, the potentialized collector (the
charged secondary source) is sharply switched away from its
connection to the primary potential source (the battery), and at
the same time it is instantly switched into a separate closed
circuit with the load. This is important: In cycle two, the
potentialized collector (with its finite amount of excess
trapped EM energy) and the load are connected in a completely
separate circuit, and one that is closed, with no connection at
all to the original source of potential (in this case, to the
battery). Specifically, this "load and potentialized collector"
circuit is completely separate from the primary source; during
cycle two the primary source (the battery) is not connected to
anything.
In other words, all we've taken from the
primary source (the battery) is current-free, force-field-free
potential gradient. So to speak, we've taken a "chunk of potential
gradient" from the source, nothing else. You simply multiply the
potential gradient's local energy density (the so-called "voltage",
which is really excess joules per coulomb) by the number of coulombs
of charge that is "activated" (that "collects" this voltage or
excess joules/coulomb) in the collector. Specifically, we have not
taken any power from the battery itself, and so we have not done any
internal work inside the battery upon its internal resistance, by a
"closed circuit electron flow" back into the battery. We have not
permitted such a flow.
Instead, we are using the activated collector as a temporary,
secondary battery. We will utilize this secondary battery in a
conventional manner to power the load, which will also kill the
secondary battery (dissipate its trapped EM energy). But that will
not affect the primary source. The primary source is never used to
directly power the load. It is only used as an infinite source of
potential gradient (i.e., as an infinite source of energy density).
The
Standard Power Extraction Circuit
The Conventional Circuit:
We digress momentarily: In the standard
electrical method, the potential source (which is a bipolarity) is
connected across the load. This connects both the external load and
the internal resistance of the battery itself in series, as the
"total circuit load." Electrons then pour through the external load
circuit and through the internal battery resistance, from the
"electron rich" polarity of the source to its "electron poor"
opposite polarity. The scattering of energy in the internal battery
resistance is actually doing work to upset the chemistry that is
maintaining the battery's charge separation (the bipolarity). In
this manner, the source's separation of charges (which is the "gate"
furnishing the potential/energy gradient) is being destroyed as the
current flows, and this in turn destroys the source of the potential
gradient.
In other words, normally we, engineers, are trained to kill the
bipolarity, which kills the potential source itself! Incredible as
it may be, we, engineers and scientists, have been trained to
utilize the free "trapped EM energy" furnished by nature through the
source, to destroy the source of the energy/potential, with the same
vigor as they power the external load! In fact, our teachers simply
have never learned any other way to do it except this deliberately
"self-destructive" manner!
A
Waterwheel Analogy
Imagine, if you will, a waterwheel that powers a mill, with a sluice
gate upstream in a river, that diverts some river water into the
sluice carrying water to the wheel when the sluice gate is opened
into the river. The diverted water flows down to the waterwheel,
turning it, and the spent water is fed back into the river below the
mill site. Now what fool would connect a pulley onto the waterwheel,
with a rope running from the pulley to the sluice gate, so that when
the wheel rotated, part of the rotational power also was utilized to
close the sluice gate and shut off the water, stopping the
waterwheel? If one did so, when the sluice gate was opened, the
waterwheel would rotate only until the sluice gate was closed,
shutting off the water. Then one would laboriously have to pay to
reopen the sluice gate again, then again, then again.
No
self-respecting "waterwheel engineer" would do such an unthinkable,
insane thing. But that's exactly what we engineers, electrical
physicists, and scientists have been trained to do! We have no
energy engineers or energy scientists at all; instead, we have all
been power engineers and power scientists. We have all been energy
source killers! In this paper, we shall try to do better, and
rectify "one of the most remarkable and inexplicable aberrations of
the scientific mind which has ever been recorded in history," as
Tesla called the conventional electromagnetics.16 By being energy
engineers, we shall only have to pay for our energy source once, and
then we shall draw as much energy from it as we wish.
External
Load Power Is Free; Only The Power In The Source Costs
Here's the magic secret of free electrical power: The power in the
external load is absolutely free, and it always has been free.17
In any load circuit, the only power you have to pay for, and have
ever had to pay for, is the power you incorrectly use to kill your
own primary source. The only power that "costs" more effort/dollars
is the power erroneously utilized inside the source to "close the
gate" and kill the primary source. Your electric power company
doesn't pay for any of the collected energy on your load circuits
that is dissipated to power your house. Instead, the power company
charges you for its own ignorance. It charges you for its insane use
of its own freely extracted electrical energy to continually kill
the bipolarity in each of its generators, thus continually killing
the free electrical source of that generator's energy.18
In any electric circuit, we can continue to indefinitely power the
external load indirectly from a source, so long as we are not so
naive as to use any of the free energy we extract from the primary
source to dissipate back inside the primary source itself and shut
it off!
And we can easily and freely multiply electrical potential. As an
example, given a single good source of potential, a hundred radial
wires can be connected to the source. The same potential will now
appear at each of the ends of the hundred wires. A
switcher/collector unit can then operate from each radial line's
end, and power external loads, without "loading" the original
primary source. This "cascading" can be continued indefinitely. A
single power plant, e.g., can power the entire electrical grid of
the United States. And a single automobile battery can power a
large, agile, electric automobile at highway speeds, with sports car
acceleration, with unlimited range, without "refueling," and with no
noxious chemical exhaust.
Obvious
Impacts
Environmentalists should immediately see that the chemical pollution
of the biosphere by mechanista and processes to obtain energy can be
dramatically reduced, to almost negligible levels. There need be no
huge oil tanker spills, for there need be no huge oil tankers. There
need be no worrisome radioactive wastes from nuclear power plants,
or abandoned hazardous nuclear plants when their life is finished,
because there need be no nuclear power plants. There need be no
noxious exhausts from jet airplanes (which are really what is
diminishing the ozone layer and punching holes in it), automobiles,
trucks, buses, innumerable coal-fired and oil-fired power plants,
etc.
The
Electronic Smog Problem
In fairness we point out that, as the usage of free electrical
energy mushrooms, we will be dramatically increasing the low-level
EM signal density of the environment, and that too is biologically
detrimental. Although beyond the scope of this paper, that
cumulative biological damage mechanism has also been uncovered by
this author. A formal paper is presently in preparation for
presentation in March 1993 at the annual meeting and conference of
the Alabama Academy of Science.19 The paper will also present an
entirely new definition of cancer, give its exact long-term
cumulative mechanism, and give an exact, scientifically proven
mechanism for eliminating cancer, leukemia, and other debilitating
diseases such as AIDS. For our purposes here, we simply state that
we understand the EM "electronic smog" biological damage mechanism,
and how to go about developing a total counter for it. Eventually,
we would see a small "counter unit" added to each power unit,
alleviating the "electronic smog" problem and preventing biological
damage.
Only
Dissipate Energy From a Collector, Not the Source
Completion of the Collection Cycle:
But to return to the completion
of our collection cycle (cycle one). During collection, we have not
extracted power from the source. That is vital. We have not moved
the gate through which our source is furnishing free energy. We have
not diminished our primary source. From our previous definitions of
potential, we have indeed extracted trapped energy from the primary
source, because we placed its "local energy density" across a
certain finite collector/mass, instead of extracting power
(dissipating energy inside the source or battery to spoil its
chemistry and deplete its charge separation).
All
Energy Is Free
Here's the incredible truth. The entire universe is filled with mind
boggling free energy everywhere, in the simplest of things. Simply
scrape your feet on the carpet, and you will collect perhaps 2,000
"volts" on your body. At that time, hidden EM energy is flowing from
every point in the universe to your body, and from your body back to
every point in the universe. We know that all macroscopic matter is
filled with stupendous amounts of electrical charge. So an
incredible river of energy -- a great flux -- is driving every
single thing, from the smallest to the largest. Opening a gate to
extract trapped EM energy is simple. Just collect a bit of charge,
or scrape your feet hard, or comb your hair briskly. All we have to
do is not be stupid and close the gate once we've got it opened!
God has been most kind. We have nothing but free energy everywhere.
All energy is furnished to us freely! It's our own blindness that
has made us into energy source killers. All we have to do is open
our eyes to the truth of nature's incredible energy bounty. We must
just freely collect that bountiful fruit from Nature's tree, instead
of chopping down the tree and killing it.
Dissipating The Collected Energy
The Work Cycle:
We focus again on cycle two. Shortly after the now-potentialized
collector is connected to the load at the beginning of cycle 2 (the
power cycle, or energy dissipation cycle, or work cycle), the
potential gradient across the potentialized collector is connected
(transferred) across the free electrons in the load circuit. We
assume that the material of the collector and the switching time
have been designed so that, shortly after switching to the
loading/work cycle, the activated/potentialized free electrons in
the electron gas in the collector reach the skin of the collector,
and are free to move as current.
So just after the beginning of cycle two, each of the free electrons
in the load circuit now is potentialized and free to move down the
wiring. Each potentialized (activated) electron has its own little
individual potential gradient across it and coupled to it, due to
the overall potential gradient from the collector. Remember, prior
to coupling to charges, this potential gradient moves through the
circuit at light speed. An EM potential gradient coupled to a
charged mass constitutes an EM force field (excess trapped EM energy
per coulomb, times the number of collecting coulombs). Now each
little free electron with its potential gradient forms a little
E-field (force/charge), and that little E-field (force/charge) is
free to move. That's all it takes to move (accelerate) the little
activated electron's mass through the load (the scatterer). We
strongly stress that the potentialized/activated electron moves
itself. It doesn't care whether or not the external battery is
attached or not. It is its own little motorboat, with its own little
engine driving it.
As the little potentialized electrons reach the load (the scatterer),
they bang and clang around in there erratically. That is, the "scatterer"
(load) causes spurious accelerations ("scatterings") of these
self-driven electrons. As is well-known, when a charge is
accelerated, it radiates photons. What actually happens is that
these little "jerked around" electrons shuck off their little
potential gradients in the load (in the scatterer, or the "jerker-arounder")
by emitting/radiating photons in all directions. Hence the heat that
is produced in the load; the heat is just these scattered photons.
The theory of calorimetry already states that all the excess energy
(on the potentialized electrons) will be dissipated as this heat
(scattered EM energy).
When all the potentialized electrons have radiated away their
potential gradients in the load (scatterer), they are no longer
potentialized. The free electron gas is again "quiescent" and no
longer potentialized/activated (again, we are talking about "on the
average" from a classical viewpoint).
Repetition and Review
Notice What We've Done:
We took some trapped EM energy density (a
chunk of potential gradient, a "voltage" before current flows) from
the source, by switching that potential gradient (energy density,
which is joules per coulomb) onto a collector (containing a certain
number of coulombs of trapped charges) where the potential gradient
activates/potentializes/couples-to these temporarily non translating
electrons. So the finite collector collected a finite amount of
excess energy [joules/coulomb x collecting (trapped) coulombs] on
its now-excited (activated) free electrons. Then, before any current
has yet flowed from the source, we switched that potentialized
collector (with its temporarily restrained but potentialized
electrons; with their finite amount of excess trapped EM energy)
away from the source and directly across the load. Shortly
thereafter, the relaxation time in the collector expires. The
potentialized electrons in the collector are freed to move in the
external load circuit, consisting of the collector and the load, and
so they do so. The scattering "shock collisions" due to the erratic
electron accelerations in the load shake off the little potential
gradients on the conduction electrons, emitting photons in all
directions, which we call "heat." In shaking off the photons, the
electrons lose their little potential gradients, hence lose their
activation (excess EM energy).
Rigorously, we have extracted some energy in trapped form, and
allowed it to dissipate in the load, "powering the load" for a
finite discharge/dissipation time and doing work.20 Contrary to the
conventional electrical power engineering, we have also done this
without doing any work inside the source to diminish its ability to
furnish potential gradient.
What Is
Energy In An Electric Circuit?
Energy in an Electric Circuit:
Here's the principle loud and clear.
Energy in an electric circuit involves only the potentialization and
depotentialization of the electron carriers in that circuit.21 It
involves only the potential gradient (the joules per coulomb)
collected by the circuit to potentialize its electrons, and the
number of coulombs of electrons that are potentialized during the
collection phase. Electric circuits simply utilize electrons as
carriers of "potential gradients," from the source to the load,
where these gradients and the activated electrons constitute excess
trapped EM energy. In the "shocking/scattering" occurring in the
load, the jerking (acceleration) of the electrons causes these
activated (trapped-energy-carrying) electrons to shuck off their
potential gradients by emitting them as scattered photons (heat).
If one is thoughtless enough to allow the primary potential source
to remain in the circuit during the "work" phase, then one is using
the potentialized electrons to also go back into the primary source
and scatter energy from its internal resistance (internal load),
thereby disorganizing the organization that was producing the source
potential and energy in the first place. If one does that, then all
the while one is getting some work (scattering of energy) in the
load, one is also steadily getting some work done inside the primary
source to steadily destroy it! Literally, one is killing the goose
that lays the golden eggs.
Continued Operations:
But back to our circuit. After we complete one
full collection/discharge cycle, we wish to continue producing work
in the external load. So we simply switch the collector back away
from the load and onto the primary source, collect some more
current-free potential, and again independently switch the collector
with its repotentialized free electrons back across the load. We can
repeat this two-cycle process to potentialize the external load and
power it as long as we wish, from a battery or other source of
potential, and never take any power at all from the primary battery.
We do not need to drain the battery or source at all, in order to
power a load, unless we attempt to power it directly. Powering the
external load is always free!
Nature has been most kind, and we have been most ignorant. You can
have all the trapped electrical energy you wish, from any source of
potential, for free. You can power all the external loads you wish,
for free, by using a collector as a secondary source, and simply
shuttling potential between the primary source and the collector.22
But you cannot have power for free from (in) the potential source.
If you allow current flow in your collection cycle, you are
depleting the separated charges inside the battery that are
furnishing the source potential.
The
Coal-Fired Locomotive
Rigorous Analogy of a Coal-Fired Locomotive.
Now here's an exact
analogy, to assist in understanding. Imagine a coal-fired train, and
a fireman shoveling coal. He has an external load/scatterer of
energy (the fire in the firebox under the boiler). He has a primary
source of potential/energy (the coal car). No fireman in his right
mind would ignite the coal in the chute of the coal bin, to try and
get some heat energy into the firebox! [That is, he would not
attempt to extract power from the source. Yet that's exactly what
all we engineers are trained to do at present.] Instead, the fireman
takes out (collects) a finite amount (a shovelful) of coal (trapped
energy). Coal per se (the potential gradient) has a certain energy
density per unit volume (trapped joules per unit volume of coal) and
the shovel (collector) has a certain volume.
Accordingly, the shovelful of coal
contains a certain amount of trapped joules of energy. In the
fireman's shovel (the collector), the energy remains in totally
trapped form, as coal not afire and without its trapped energy being
dissipated as work. [He doesn't act like a fool and ignite the coal
in the shovel either!] He then throws that shovel of coal (collected
trapped energy) onto the fire (scatterer), completely separately
from the coal bin/source. He continues to repeat his shoveling
cycle, and each shovelful of coal added to the fire dissipates
additional energy, powering the load.
The Free
Energy Principle
All potential gradient (trapped excess energy density) is free for
the taking23. The potential is due to the violent VPF exchange
between the vacuum and the separated bipolar charges furnishing the
source potential gradient. The energy of the entire universe is
flowing through that source potential. You can have as much of this
internal VPF flux energy (potential) as you wish, as often as you
wish, so long as you don't demand current (which is power, or the
rate at which the energy is being freed and dissipated). It's really
simple. You can have all the trapped energy you wish, from any
source. You cannot connect to the source and start to dissipate the
energy as power, however, without starting to close the "gate" from
which your free trapped energy is coming.
In other words, here's the iron rule: If you draw current, you kill
the bipolarity gate furnishing the potential gradient (source of
energy density). In that case, you kill the source. If you do not
draw current, you do not kill the bipolarity gate and you do not
shut down the source. In that case, you can continue to "use" it and
extract trapped EM energy from it forever.
Definitions Again
Definitions:
I'll put down some simple equations, that may help to
explain it more exactly. First we repeat some definitions.
Energy is any ordering imposed upon the virtual particle flux of
vacuum. EM energy is any ordering imposed upon the virtual photon
flux of vacuum. Static energy is an ordering (a template) which is
stationary with respect to the external observer. Dynamic energy is
an ordering (a template) which is not stationary with respect to the
external observer.
Potential: Any ordering imposed upon the virtual particle flux of
vacuum. Scalar potential is an ordering (template) that is not
moving with respect to the external observer. Vector potential is an
ordering (template) that is moving with respect to the external
observer.
The scalar EM potential is any static (with respect to the external
observer) ordering imposed upon the virtual photon flux of vacuum.
Etc.
Note again that energy and potential have exactly the same
definition. Potential is in fact trapped energy. Scalar EM potential
is static EM energy (to the external observer) or trapped
(collected) EM energy. In other words, if one takes off a
differential of potential onto a fixed number of coulombs, one takes
off a certain magnitude of trapped EM energy. In other words, one
takes out a shovelful of coal from the coal car.
Importance of Separation of Charges
We Must Not Dispel the Separation of Charges In Our Source:
The
difference in our coal-fired train analogy and our electrical
circuit is that, in the coal train, the coal in the coal car is not
automatically and continually replenished. Also, the coal in the
coal car has already been collected by the mass of the coal car, so
it is not infinite. In the electrical circuit, the potential
gradient in the primary source is continually replenished,
automatically, and it is infinite (though it has a finite energy
density). The reason is simple. EM potential (in the normal sense)
is actually a virtual photon flux exchange between the vacuum (the
entire vacuum, all over the universe) and a charged particle or
collection of charged particles.24Thus the potential (gradient) is
a powerful energy flux, pumped by the vacuum and the entire
universe, that continues automatically, so long as we do not allow
the collected charges in our bipolarity source to be dissipated. In
terms of a battery, we achieved separation of charges inside the
battery by chemical action, and we paid for that initially.
Once separated, the charges essentially
stay separated (because of the chemistry) unless we foolishly do
something to dissipate them, such as upsetting the chemistry, so
they are no longer separated positive from negative. So if we don't
do anything to these separated charges, they continue to be driven
by their fierce exchange of virtual photon flux with the
vacuum/universe. If we then simply extract some of that flux
exchange, without moving the charges, we are directly "gating"
trapped EM energy from the vacuum/charged particle VPF exchange.25
The
Potential Is Infinite And So Is Its Energy Content
You Can't Dip The Ocean Dry With a Spoon:
Let's say that another
way. The charged particles in our potential source are in a
constant, seething, equilibrium exchange of trapped EM energy with
the entire universe. That energy exchange is so enormous that, if we
gate some of it out to collect on some other "temporarily frozen"
charges and potentialize/activate them, the vacuum flux doesn't even
miss it. It's like dipping a spoonful of water out of the restless
ocean. The hole is instantly filled, and the water replenished. We
can dip with that spoon as much as we wish, and the ocean will never
run dry, but will simply continue to furnish us water, spoonful by
spoonful.
The same is true in our electric circuits. We can have all the
potential (trapped EM energy density) we wish, for free, from a
single source, so long as we do not allow work to be done inside the
source to close off our "gate" and kill our primary source.
The
Twisted Concept of Voltage
Before We Develop Some Pseudo-Equations:
In the equations we wish to
develop, we have one problem, due to the lack of insight of
conventional electrical physicists. That is, they have insisted upon
"measuring" and expressing both the infinite potential (nondissipated)
and a certain quantity of potential (dissipated) in volts. So they
say "a potential of so many volts." That's nonsense, and totally
erroneous. Rigorously, a voltage is a drop or a dissipation of so
much (a finite amount of) collected excess potential/energy. You
"measure" the voltage in a voltmeter by impressing a potential
gradient upon the electron gas in the circuitry, wherein you collect
or get in your voltmeter so much [(joules/coulomb) x coulombs]. A
tiny current (coulombs/second) from this internal collection then
flows for a finite time through the resistance of the voltmeter. So
you dissipate (joules/coulomb) x (coulombs/second) x (seconds),
which gives a certain amount of energy dissipated as work in moving
the needle of the voltmeter. The voltmeter is calibrated so that it
effectively indicates the collected energy per coulomb that was
dissipated, and it calls that entity voltage.
It involves a finite amount of energy
that has already been dissipated as work, and it's a measure of the
local energy density of the potential in terms of joules/coulomb. It
is not a measure of the potential proper. It's after the fact; the
extracted (collected) potential gradient it actually refers to
existed in the past, before the work (dissipation of the collected
trapped energy) was done. To refer to the potential before its
dissipation as "voltage" is precisely the same as confusing the
future with the past. A "potential (difference) of so many volts" is
actually a statement that "a potential difference of so much energy
per coulomb" could be dissipated in a load, if it were connected to
the load so that a finite amount of energy was collected, and this
finite load-collection was allowed to dissipate as power
(volts/coulomb x coulomb/sec) for a finite time, yielding work. It's
even worse, but it would take a textbook to straighten out this one
error in EM theory.
So we'll leave it at that, and we'll adapt the notion of potential
the way it is corrupted in electrical circuit theory. There it's
used not really as energy, but rather as excess energy per coulomb
of potentialized charge. I apologize for that difficulty, which is
not of my own making, but I must use the conventional notion if we
are to greatly clarify the pseudo equations.
The
Equations of Free Energy
The Pseudo-Equations:
Let us use the following subscripts and letter
convention, and develop the nomenclature needed:
T = trapped d = dissipated or
dissipating
m = translated (moving) K = energy
V = volts = potential drop (potential dissipated) = previously
collected potential radiated away as heat in a load, doing work
on the load in the process. Unfortunately, we shall also have to
speak of a potential gradient that is not being dissipated, so
we shall have to speak of "trapped volts" which is erroneous,
but complies with the common usage.
f = electrostatic scalar potential. Coul = coulombs
i = amperes = Dissipating potentialized coulombs per second
flowing, so amps are something translating, always. Amps are
excited coulombs, per second, that are dissipating their
excitation. With superconductivity excluded, you only have amps
when you have a potential drop across a load. So we will speak
of amps as "dissipating," meaning that potentialized electrons
are traveling through a load, dissipating their activation
(gradients) in the load by radiating scattered photons (heat).
n = number of electrons in a coulomb = 6.3 x 1018
electrons/coulomb
Here are the pseudo equations
(superconductivity is excluded):
ampm = could/sec = n electronsm/sec
= n electronsd/sec [1]
Df = VT (as conventionally referred to). It would be volts if
all [2] of it were dissipated, but it is not yet dissipated, so
it is sort of "trapped volts". Erroneous, but the common use. So
we will speak (somewhat distastefully) of "trapped volts" and
"dissipated volts."
Vd x ampd x sec = watts x sec = power x time = work = Kd [3]
Vd x could/sec x sec = (work) = Kd [4]
In the switching, we switch KT to Kd so
KT Þ Kd [5]
But VT x coulT = KT [6]
Or
[VT] = [KT] / [coulT] = trapped energy/trapped coulomb [7]
[KT] = [VT] x [coulT] = amount of trapped energy, each cycle [8]
So that's what we were getting at. The
amount of trapped energy you can transfer (in other words, how much
coal you get in one shovelful) depends upon the number of trapped
electrons you have in the trapped free electron gas in the
collector, and the potential gradient you apply to those trapped
coulombs to potentialize them.
Relaxation Time and Semiconductors
Relaxation Time:
The time it takes for the free electrons in a
conductor (or material) to reach the skin of the wire after
potential is applied, is, of course, called the relaxation time.
During that time, the free electrons in the gas are "trapped"
insofar as producing current (dissipation of the potential) is
concerned. However, immediately after the relaxation time ends,
current begins and dissipation of the trapped energy begins.
In copper, the relaxation time is incredibly rapid. It's about 1.5 x
10-19 sec. However, in quartz it is about 10 days! So as you can
see, we need to get somewhere in between these two values, and so we
will have to "mix" or "dope" materials. We must get a sufficiently
long relaxation time so that we can switch and collect comfortably
in cycle one, then switch into cycle two for dispersion of the
freely collected energy in the collector. However, the relaxation
time we get must also be short enough to allow quick discharge in
the load, as soon as we switch the primary source away from the
collector. Actually, we need a degenerate semiconductor material
instead of plain copper.
Degenerate Semiconductor Material:
A semiconductor material is
intermediate between a good conductor and an insulator. It's a
nonlinear material, and doped. A degenerate semiconductor material
is one which has all its conduction bands filled with electrons, and
so it thinks it is a conductor. That is, a degenerate semiconductor
is essentially a doped conductor, so to speak. As you can see, we
can increase the relaxation time in our "conductors" connected to
the source by making them of degenerate semiconductor material. What
we're talking about is "doping" the copper in the wire, and in the
collector, so that we can have plenty of time to collect, and
switch, and discharge, and switch, and collect, etc.
Now in a doped conductor (degenerate semiconductor), we can tailor
the relaxation time by tailoring the doping. We must dope the copper
before we make the wire. Why would we wish to do that? We want to
overcome the single problem that so far has defeated almost all the
"overunity" researchers and inventors.
WHEN YOU CONNECT TO A SOURCE, YOU CAN ONLY EXTRACT CURRENT-FREE
POTENTIAL -- FREE "TRAPPED EM ENERGY" -- DURING THE ELECTRON
RELAXATION TIME IN THE CONNECTING CONDUCTORS AND SUCCEEDING CIRCUIT
COMPONENTS. AFTER THAT, YOU'RE STEADILY EXTRACTING POWER, AND THE
ENERGY EXTRACTED FROM THE SOURCE IS BEING PARTIALLY DISSIPATED IN
THE RESISTANCE/LOADING OF THE CIRCUIT, AND PARTIALLY DISSIPATED IN
THE INTERNAL RESISTANCE OF THE SOURCE. IN THE LATTER DISSIPATION,
YOU'RE ALSO DISSIPATING YOUR SOURCE BY DOING WORK ON IT INTERNALLY
TO KILL IT.
Good Copper Wire:
Bane of Overunity Inventors: Many destitute
inventors, tinkering and fiddling with overunity devices, finally
get something (a circuit or device) that does yield more work out
than they had to input. At that point, they usually conclude that
it's simply the specific circuit configuration and its conventional
functioning that produces the overunity work. However, usually as
soon as this configuration is more carefully built with very good
materials, boom! It isn't overunity anymore. The inventors and their
assistants then desperately bang and clang away, getting more
frustrated as the years pass. The investors get mad, sue for fraud,
or get in all sorts of squabbles. The scientists who tested it and
found it wanting, pooh-pooh the whole thing as a scam and a fraud,
or just a seriously mistaken inventor. Scratch one more "overunity"
device.
Most of these inventors got their successful effect (and possibly
erratically) when they were struggling with inferior, usually old,
usually corroded materials. Actually, the more inferior, the better.
The more contaminated/doped, the better!
The moment you wire up your circuit with good copper wire connected
between the battery or primary source and any kind of load including
the distributed circuitry loading itself, you can forget about
overunity. You will lose it in the copper, after the first 1.5 x
10-19 second!
Think of a really good conductor such as copper as an essentially
linear material. Linear means energy conservative. Overunity can
only be done with a highly nonlinear effect. So your "conductors"
have to be made of nonlinear materials. In fact, they have to be
made of degenerate semiconductor material. For the type of circuitry
we are talking about, the copper has to be doped and then made into
"doped copper" wiring. You also have to utilize the primary battery
only to potentialize a collector (secondary battery/source), and
then use this secondary battery source to conventionally power the
load while also killing itself.
The Wiring And the Collector Must Be of Degenerate Semiconductor
(DSC) Material.26
A good materials scientist/engineer, together with
a decent electrodynamicist, can readily design and tailor some doped
copper wiring so that the material in the wiring is a degenerate
semiconductor material, with a target (desired) relaxation time.
That's what you should use to make the wiring to connect up your
source to the collector with, and that type of material is also what
you use in your collector. You can use either a coil or a capacitor
as the collector, but its "conductive" material has to be degenerate
semiconductor material -- in short, it must be doped to have the
proper relaxation time. From the collector to the load, however,
obviously you want to use a good conductor material. Ordinary copper
will do nicely there.
Once you do that, you're in business. When making the DSC material,
simply tailor the relaxation time to something which is easily
switched. For example, take one millisec. With a relaxation time of
that long, switching is easy. In fact, one could even use good
mechanical switching. Or easily use inexpensive ordinary solid state
switching, without having to go all the way to nanosecond switching.
Then, in the collector, you calculate the number of "trapped
coulombs" you have. Take the "trapped voltage" (current-free
potential's energy density per coulomb) you extract from the source
during the electron relaxation time after the collector is
connected. Multiply the number of trapped coulombs in the collector
by the trapped voltage during collection, and you have the amount of
energy in joules that you extract FOR FREE, without paying for it,
from the source during every collection cycle.
Sources,
Collectors, and Power
Tapping Vacuum Energy.
You're getting the excess electrical energy
directly from the vacuum, as we briefly pointed out above. The
vacuum will freely replenish all the "trapped voltage" you extract
from the primary source during the electron relaxation time. It
won't replenish a single bit of "dissipated voltage" (power) you
extract from the source.
Note that the same considerations apply in the collector. It's got
to have a somewhat longer electron relaxation time. Its electrons
stay "unrelaxed" during the collection cycle, and allow for some
additional switching time to connect to the load. The "trapped
voltage" across the collector multiplied by the number of trapped
coulombs in it, gives the number of joules of FREE EM ENERGY you
extract and get into and onto the collector (the shovel). In other
words, that's your "shovelful of coal." You then throw the
"shovelful" onto the fire/load -- you simply disconnect the
collector from the primary source and connect it across the external
load. The collector (secondary battery) now powers the load and its
own internal resistance, "killing" itself while furnishing the
energy for powering the external load as well.
The Source Can Be Almost Anything:
You can use as a source a simple
elevated wire, to "tap" potential from the 200-300 volts/meter
between earth and ionosphere. Here again, you need to utilize
calibrated, doped wire.
Finally, you must adjust the repetition switching in accordance with
the discharge time through the load. In other words, you have a
serial process as follows:
(1) extract trapped
energy (potential) from the source onto the collector,
Dt1
(2) Switch the collector off the source, onto the
load, during time Dt2
(3) Wait while the collected energy in the collector
discharges through the load, during time
Dt3
(4) Switch the collector back off the load and onto
the potential source, during time
Dt4. That completes one
cycle
The serial timing simply is [Dt1 +
Dt2 +
Dt3 +
Dt4].
If you balance all the doping and the materials design, and
correlate the switching, you can get all the free energy you wish.
Properly utilized, a single car battery can be used to power an
electric automobile indefinitely. Or even to power a battleship. In
the real world, of course, you will inevitably have a tiny bit of
loss as you go, because there's a finite (though high) resistance
between the two poles of your battery. Handling that is a piece of
cake. Simply run a separate little collection circuit to collect a
little bit of trapped EM energy from the slowly leaking source, and
ever so often feed the collected energy back into the battery as
power, to "reseparate" the charges (charge the battery) and replace
the small amount of the primary source's potential gradient that has
been lost. The battery, load, and "trickle charger" then become a
closed-circuit free-energy source that will last for years and
years.
Limited Only By One's Imagination:
Of course you can see many
variants; this is just the "master key." You can have multiple
collectors, collecting trapped energy simultaneously or in sequence
off a single source, and pooling their collected energy to more
powerfully power the load. You can utilize a very high "voltage",
such as in the Swiss electrostatic overunity device, to increase the
energy collected per coulomb in each switching (in each shovelful)
in accord with equation [8]. For a battery, you can set a separate
little collector/load device to trickle-charge the battery,
overcoming the small normal "leakage current" that does occur in
batteries and in real circuits and devices. The opportunities are
endless. You can put in a unit to take mostly only power-free energy
from the "power line" feeding your business or home, reducing your
utility bill by -- say -- 90%. Or you can simply build a small home
power unit to do the whole job, for only a few hundred dollars. This
simple secret can be used to power the world, cheaply and cleanly,
and to clean up the biosphere.
Conclusion
Well, there you have it. I've given you the benefit of what required
most of my adult life to discover. The definitions advanced in this
paper are rigorous. It took years of sweat and tears to come up with
them. They're simple, but they will change your entire understanding
of electromagnetics, power, and energy once you grasp them. Please
read them, and ponder them, several times. One or two readings will
not be sufficient to fully grasp what is said here.
Also, hopefully, by this time, the reader is beginning to experience
the same emotions as I experienced when I finally discovered how
simple it all really was. First one wants to laugh for about two
hours at how truly ignorant we've all been. Then one wants to cry
for about two hours for the same reason. This could all have been
done a century ago, if we had ever really understood
electromagnetics.
We've had this electromagnetics around for over 100 years --
Maxwell's book was published in 1873. We got it wrong, starting
right with Maxwell and his use of the material ether, which was
almost universally assumed at the time. Still, by using quaternions,
Maxwell succeeded in packing a great deal more in the model than
even he himself recognized. When the vector aspects interacted to
form a zero resultant translationally, those active interactants
were still in there and still fighting and interacting. The scalar
component of the quaternion remained, and infolded those struggling
vectors and functions of them inside itself. In short, it captured
the case where the electromagnetic energies are involved in
translation actions which nullify each other translationally
(electromagnetically). However, the energies are still in there in
the continuing interactants inside the zero vector resultant. As
such, they are trapped EM energy. And it is the trapped EM energy
inside a mass -- not the mass per se -- which is responsible for
gravitation. In other words, Maxwell's theory already correctly
captured the unification of the gravitational field and the
electromagnetic field in 1873.
Then Heaviside et al forced Maxwell's theory into a vector
framework, throwing out the scalar component, and discarding the
unification of gravitation and electromagnetics along with it.
Serious errors were made and still exist in many of the fundamental
definitions; in fact, many of them aren't definitions at all. Nearly
every engineer and physicist can readily calculate potentials --
all, of course, on the "dissipation" side where the potentials are
actually the amount of potential that was collected upon a collector
and then dissipated. I could find hardly a single physicist who
really knew what a scalar potential was prior to a finite amount
being collected and dissipated as voltage. Yet 99% of them firmly
believed they understood the potential.
So now you have the results of this researcher's long and arduous
quest for the golden fleece. Please go forward with it, to make this
a better and cleaner world for everyone.
Just remember that the control and use of energy is personal power.
The control and use of absolute energy is the control and use of
absolute personal power. In the old adage, power corrupts and
absolute power corrupts absolutely.
Please use it wisely.
NOTES
AND REFERENCES
1. For a good discussion of the
modern quantum mechanical view of the vacuum, see I. J. R. Aitchison, "Nothing's plenty: the vacuum in modern field
theory," Contemporary Physics, 26(4), 1985, p. 333-391. See also
T. D. Lee, Particle Physics and Introduction to Field Theory,
Harwood Academic Publishers, New York, 1981 -- particularly
Chapter 16, "Vacuum as the source of asymmetry." See Timothy
Boyer, "The classical vacuum," Scientific American, Aug. 1985,
p. 70; Walter Greiner and Joseph Hamilton, "Is the Vacuum really
Empty?", American Scientist, Mar.-Apr. 1980, p. 154; Jack S.
Greenberg and Walter Greiner, "Search for the sparking of the
vacuum," Physics Today, Aug. 1982, p. 24-32; Richard E. Prange
and Peter Strance, "The superconducting vacuum," American
Journal of Physics, 52(1), Jan. 1984, p. 19-21; R. Jackiw and
J.R. Schrieffer, "The decay of the vacuum," Nuclear Physics B,
Vol. 190, 1981, p. 944. See Paul Davies, Superforce, Simon and
Schuster, 1984 for a layman's overview of modern physics,
including the modern view of the vacuum.
2. E. T. Whittaker, "On the partial differential equations of
mathematical physics," Mathematische Annalen, Vol. 57, 1903, p.
333-355. Since the scalar potential actually consists totally of
a set of hidden bidirectional EM waves, then scalar
interferometry is possible, and not just an oxymoron as it would
seem without considering the inner wave structure of the scalar
potential. Two scalar potentials (each of which is a multi-biwave
set) can interfere; it is just a special kind of multiple wave
interferometry between their internal wave compositions. This is
a major point of profound impact on physics. Whittaker in fact
showed that all classical EM could be replaced by such scalar EM
potential interferometry. See E. T. Whittaker, "On an expression
of the electromagnetic field due to electrons by means of two
scalar potential functions," Proceedings of the London
Mathematical Society, Series 2, Vol. 1, 1904, p. 367-372.
Further, scalar interferometry has been proven; today it is
called the Aharonov-Bohm Effect. See Y. Aharonov and D. Bohm,
"Significance of Electromagnetic Potentials in the Quantum
Theory," Physical Review, Second Series, 115(3), Aug. 1, 1959,
p. 458-491. For confirmation and discussion, see Bertram
Schwarzschild, "Currents in normal-metal rings exhibit
Aharonov-Bohm Effect," Physics Today, 39(1), Jan. 1986, p.
17-20. For an extensive discussion of the Aharonov-bohm effect
and an extensive list of references, see S. Olariu and I.
Iovitzu Popescu, "The quantum effects of electromagnetic
fluxes," Reviews of Modern Physics, 57(2), April 1985. Modern
scientists have generally been unaware of the inner wave
structure of the interfering potentials and have utilized only
quantum mechanical theory for the interference. Consequently,
they have been able to experimentally establish the AB effect
for only a few thousand Angstroms distance. With the Whittaker
formulation, the AB effect becomes distant-independent, because
the necessary potentials can be fabricated as laser-like beams,
simply by assembling the proper Whittaker multibeam set. Also,
Ignatovich pointed out that the Schroedinger potential can also
be decomposed into just such an internal bidirectional EM wave
set. See V.K. Ignatovich, "The remarkable capabilities of
recursive relations," American Journal of Physics, 57(10), Oct.
1989, p. 873-878.
3. See Richard W. Ziolkowski, "Exact Solutions of the Wave
Equation With Complex Source Locations," Journal of Mathematical
Physics, Vol. 26, 1985, p. 861; "Localized Transmission of Wave
Energy," Proc. SPIE, Vol. 1061, Microwave and Particle Beam
Sources and Directed Energy Concepts, 1989, p. 396-397;
"Localized Transmission of Electromagnetic Energy," Physical
Review A, Vol. 39, p. 2005; "Localized Wave Transmission Physics
and Engineering," Physical Review A, 1992, (in Press);
"Localized wave transmission physics and engineering," Proc.
SPIE Conference on Intense Microwave and Particle Beams II, Los
Angeles, CA, vol. 1407, Jan. 1991, p. 375-386. See Richard
W.Ziolkowski, Amr M. Shaarawi, and Ioannis M. Besieris, Nuclear
Physics B (Proc. Suppl.), Vol. 6, 1989, p. 255-258; R.W.
Ziolkowski, and D.K. Lewis, D.K., "Verification of the Localized
Wave Transmission Effect," Journal of Applied Physics, Vol. 68,
1990, p.6083; Richard W. Ziolkowski, Ioannis M. Besieris, and
Amr M. Shaarawi, "Localized Wave Representations of Acoustics
and Electromagnetic Radiation," Proceedings of the IEEE, 79(10),
Oct. 1991, p. 1371-1378; I.M. Besieris, A.M. Shaarawi, and R.W.
Ziolkowski, "A bidirectional travelling plane wave
representation of exact solutions of the scalar wave equation,"
Journal of Mathematical Physics, 30(6), 1989, p. 806; A.M.
Shaarawi, I.M. Besieris, and R.W. Ziolkowski, "A novel approach
to the synthesis of nondispersive wave packet solutions to the
Klein-Gordon and the Dirac equations," Journal of Mathematical
Physics, 31(10), 1990, p. 2511; "A nondispersive wave packet
representation of photons and the wave-particle duality of
light," UCRL-101694, Lawrence Livermore National Laboratory,
Livermore, CA, 1989; "Diffraction of a classical wave packet in
a two slit interference experiment," UCRL-100756, Lawrence
Livermore National Laboratory, Livermore, CA 1989; "Localized
energy pulse trains launched from an open, semi-infinite,
circular waveguide," Journal of Applied Physics, 65(2), 1989, p.
805; R.W. Ziolkowski, D.K.Lewis and B.D.Cook, "Experimental
verification of the localized wave transmission effect,"
Physical Review Letters, 62(2), 1989, p. 147; R.W. Ziolkowski
and D.K. Lewis, "Verification of the localized wave transmission
effect," Journal of Applied Physics, 68(12), 1990, p. 6083; M.K.
Tippett and R.W. Ziolkowski, "A bidirectional wave
transformation of the cold plasma equations," Journal of
Mathematical Physics, 32(2) 1991, p. 488; A.M. Vengsarkar, I.M.
Besieris, A.M. Shaarawi, and R.W. Ziolkowski, "Localized energy
pulses in optical fiber waveguides: Closed-form approximate
solutions," Journal of the Optical Society of America A, 1991.
4. For a precise statement of the distortion correction theorem,
see Amnon Yariv, Optical Electronics, 3rd Ed., Holt, Rihehart
and Winston, New York, 1985, p. 500-501.
5. Both wave and antiwave co-exist in the vacuum simultaneously,
forming a stress wave. The entity that is stressed is the rate
of flow of time. In the common interaction with matter, the
time-forward half of the stress wave normally interacts with the
electron shells of the atom, giving electron translations
forces. The time-reversed or anti-wave half interacts with the
nucleus, giving the Newtonian 3rd law reaction (recoil) forces.
The so-called "EM wave" in vacuum is a gravitational wave. It is
a wave of oscillation of the rate of flow of time. It is rather
like a sound wave in air, as Tesla pointed out, and it is a
longitudinal wave, not a transverse "string" wave.
6. As pointed out by Nikola Tesla. Tesla was correct, and all
the textbooks with their transverse "string" waves are in error.
There are no strings in the vacuum!
7. E.g., see Clayton R. Paul and Syed A. Nasar, Introduction to
Electromagnetic Fields, 2nd Ed., McGraw-Hill, New York, 1982, p.
113.
8. E.g., see Clayton R. Paul and Syed A. Nasar, ibid., p.
100-101. See also Raymond A. Serway, Physics For Scientists And
Engineers, With Modern Physics, Saunders College Publishing,
Philadelphia, PA, 3rd Ed., Updated Version, 1992, p. 752-755.
9. Sommerfield's theory of metallic conduction was based on
Drude's concept that the outer valence electrons of a conductor,
which do not form crystal bonds, are free to migrate through the
crystalline lattice structure, and so to form an electron gas.
At room temperature, by quantum mechanical considerations, these
free electrons are moving randomly, but at an average velocity
on the order of 106 meters per sec. E.g., see Martin A. Plonus,
Applied Electromagnetics, McGraw Hill, New York, 1978, p. 54-58,
62-3, 376-7. If you wish to know just how much power exchange is
driving the collisions of the electron gas in a copper wire,
here is an illustration. In one cubic centimeter of copper wire,
the power exchange in and out of the electron gas is some 4
billion billion watts. That's the equivalent of 4 billion large
electric power plants, each of 1,000 megawatt capacity. And one
cubic centimeter of copper is a lump about the size of the end
of our little finger.
10. E. g., see Raymond A. Serway, ibid., p. 743-744 for a
discussion and calculation of the electron drift velocity in
copper.
11. Richard P. Feynman, Robert B. Leighton, and Matthew Sands,
The Feynman Lectures on Physics, Addison-Wesley, New York, Vol.
1, 1963, p. 2-4. In the classical EM theory launched by Maxwell
and later modified by Heaviside et al, this problem did not
exist for the original theoretical formulation. In that
formulation by Maxwell, and continued by Heaviside, a material
ether is assumed for the model. The Michelson-Morley experiments
of 1887 destroyed the notion of the material ether, but the
classical electromagnetics model has never been corrected to
rectify its very serious foundations flaw in this respect.
12. Robert Bruce Lindsay and Henry Margenau, Foundations of
Physics, Dover Publications, New York, 1963, p. 283-287. Note on
p. 283 that a "field of force" at any point is actually defined
only for the case when a unit mass is present at that point. In
spite of this, most classical electrodynamicists continue to
adhere to the notion that the EM field exists as such in the
vacuum, but do admit that physically measurable quantities such
as force somehow involve the product of charge and field. E.g.,
see J.D. Jackson, Classical Electrodynamics, 2nd Ed., John Wiley
& Sons, New York, 1975, p. 249. Note that holding such a concept
is tantamount to holding on to the material ether, and assuming
that the vacuum itself is "measurable" or "observable."
13. The formula F = ma is simply an algorithm for calculating
the magnitude of the force. It states that "the magnitude of the
force is equal to the magnitude of mass that is accelerating,
multiplied by the magnitude of the acceleration." No such
"equals" formula is a definition; it is only a calculational
algorithm.
14. This falsifies one of the assumptions in the common notion
of the scalar potential; that its gradient in vacuum is a force
field. Let us falsify another part of the conventional concept
of the potential. Take the notion of forcibly pushing in
"against the field" of a trapped charge, a unit charge from
infinity. At any point you stop, the work n you have done on the
unit charge is equal to the value of the potential, so it is
said. Actually, you pushed in a one-coulomb collector, and have
collected and dissipated as work n joules of energy on that one
coulomb. In other words, the energy density of the potential
there, if collected and dissipated on a collector, is n, where n
is joules per coulomb (NOT joules!). To prove it: suppose we go
out on 10,000 radials from that point, and push in from infinity
10,000 unit charges from infinity. Then, the total work done
"against the potential gradient ("field", in common language) is
now 10,000 n. This makes no sense at all from the conventional
view (which carefully refrains from multiple collectors!). It
makes good sense from our view of the potential as having
infinite energy but a finite energy density. In that case, the
more collectors, the more energy collected, for dispersal as
work.
15. For a discussion, see Y. Aharonov and D. Bohm, 1959.
16. Nikola Tesla, "The True Wireless," Electrical Experimenter,
May 1919, p. 87.
17. The power in the load is always the time rate of dissipation
of energy that has just been freely collected by the load for
dissipation.
18. One can foresee a day in the not too distant future when any
power company continuing to do such an unthinkable thing will
have a class action suit brought against it by its customers!
19. T. E. Bearden, "Mechanism for Long-Term Cumulative
Biological Effects of EM Fields and Radiation," March 1993 (in
preparation).
20. Precisely analogous to a heat pump's operation - which as is
well-known can readily be "over unity" in its efficiency. The
maximum efficiency of the heat pump is about 8.22. E.g., see
David Halliday and Robert Resnick, Fundamentals of Physics, 3rd
Edition Extended, John Wiley and Sons, New York, 1988, Volume 1,
p. 510-519. Good heat pumps normally have about 4.0 efficiency.
21. External power in an electric circuit refers to the
dissipation rate (in the circuit's external load) of the
potential gradients on the activated/potentialized electrons.
Internal power refers to the dissipation rate in the circuit's
bipolarity source.
22. We call strong attention to T.W. Barrett, "Tesla's Nonlinear
Oscillator-Shuttle-Circuit (OSC) Theory," Annales de la
Fondation Louis de Broglie, 16(1), No. 1, 1991, p. 23-41. In
this important paper, Barrett shows that a higher topology EM,
such as quaternion EM, allows many things to be accomplished
with circuitry that are not apparent to a conventional vector or
tensor analysis of that circuitry. He also shows the Nikola
Tesla's circuits accomplished this higher topological
functioning.
23. It is easy to test this. Connect several different wires to
a single source of potential gradient. With respect to ground,
the end of each one of those wires has the same potential
gradient as does the original source with respect to ground. If
you connect 10 wires to a single "100-volt" potential gradient
source, you will have ten 100-volt potential gradients appear.
You can use each of these ten potential gradients as a primary
source. From each of these new primary sources, you can branch
ten more, and now have a hundred potential gradient sources. You
can treat each of these hundred new sources now as a primary
source. To each one, you can add a switcher, collector, and
external load, and drive all 100 loads. Or instead, you can put
ten switcher/collector/external load circuits with each of the
hundred new primary sources, and power all 1,000 external loads.
Energy/potential is free from any source, so long as you do not
demand power from the same source.
24. Per Whittaker and Ziolkowski, this VPF exchange -- from
consideration of its wave aspects -- consists of a harmonic
series of bidirectional waves.
25. We are easily permitted to have free energy and violate the
"local energy conservation law for a closed system." This is
because the system is not closed, and so instead we must apply
local energy conservation for an open system with a hidden
source. In any given time interval, the energy taken (scattered)
from the system as external work cannot exceed the sum of the unscattered trapped energy that was in the system initially and
the unscattered energy that flowed into the system during that
time interval.
26. You can actually do away with the separate collector, and
utilize the doped copper DSC material itself as the collector.
However, you will not be able to collect nearly so much energy
in each collection cycle, for dissipating in the load in the
subsequent work cycle.
Go Back
|


