|
|
|
|
by John Gribbin from SkyBooksUSA Website
The foundation was laid by the German physicist Max Planck, who postulated in 1900 that energy can be emitted or absorbed by matter only in small, discrete units called quanta.
Also
fundamental to the development of quantum mechanics was the
uncertainty principle, formulated by the German physicist Werner
Heisenberg in 1927, which states that the position and momentum of a
subatomic particle cannot be specified simultaneously.
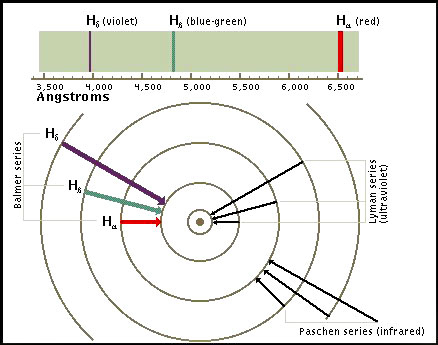
Spectral Lines of Atomic Hydrogen
When an electron makes a transition from one energy level to another, the electron emits a photon with a particular energy.
These photons are then observed as emission lines using a spectroscope. The Lyman series involves transitions to the lowest or ground state energy level.
Transitions to the second energy level are called the Balmer series. These transitions involve frequencies in the visible part of the spectrum.
In this frequency range each transition is characterized by a
different color.
In the late 19th and early 20th centuries, however, experimental findings raised doubts about the completeness of Newtonian theory. Among the newer observations were the lines that appear in the spectra of light emitted by heated gases, or gases in which electric discharges take place.
From the
model of the atom developed in the early 20th century by the English
physicist Ernest Rutherford, in which negatively charged electrons
circle a positive nucleus in orbits prescribed by Newton's laws of
motion, scientists had also expected that the electrons would emit
light over a broad frequency range, rather than in the narrow
frequency ranges that form the lines in a spectrum.
In his book Elementary Principles in Statistical
Mechanics (1902), the American mathematical physicist J. Willard
Gibbs conceded the impossibility of framing a theory of molecular
action that reconciled thermodynamics, radiation, and electrical
phenomena as they were then understood.
The first development that led to the solution of these difficulties was Planck's introduction of the concept of the quantum, as a result of physicists' studies of blackbody radiation during the closing years of the 19th century. (The term blackbody refers to an ideal body or surface that absorbs all radiant energy without any reflection.)
A body at a moderately high temperature - a "red heat" - gives off most of its radiation in the low frequency (red and infrared) regions; a body at a higher temperature - "white heat" - gives off comparatively more radiation in higher frequencies (yellow, green, or blue). During the 1890s physicists conducted detailed quantitative studies of these phenomena and expressed their results in a series of curves or graphs.
The classical, or prequantum, theory predicted an altogether different set of curves from those actually observed.
What Planck did was to devise a mathematical formula that described the curves exactly; he then deduced a physical hypothesis that could explain the formula.
His
hypothesis was that energy is radiated only in quanta of energy hu,
where u is the frequency and h is the quantum action, now known as
Planck's constant.
He used Planck's concept of the quantum to explain certain
properties of the photoelectric effect - an experimentally observed
phenomenon in which electrons are emitted from metal surfaces when
radiation falls on these surfaces.
The higher the frequency of the incident radiation, the greater is the electron energy; below a certain critical frequency no electrons are emitted. These facts were explained by Einstein by assuming that a single quantum of radiant energy ejects a single electron from the metal.
The energy
of the quantum is proportional to the frequency, and so the energy
of the electron depends on the frequency.
He assumed, on the basis of experimental evidence obtained from the scattering of alpha particles by the nuclei of gold atoms, that every atom consists of a dense, positively charged nucleus, surrounded by negatively charged electrons revolving around the nucleus as planets revolve around the sun.
The classical electromagnetic theory developed by the British physicist James Clerk Maxwell unequivocally predicted that an electron revolving around a nucleus will continuously radiate electromagnetic energy until it has lost all its energy, and eventually will fall into the nucleus. Thus, according to classical theory, an atom, as described by Rutherford, is unstable.
This difficulty led the Danish physicist
Niels Bohr, in 1913, to postulate that in an atom the classical
theory does not hold, and that electrons move in fixed orbits. Every
change in orbit by the electron corresponds to the absorption or
emission of a quantum of radiation.
For more complex atoms, only approximate solutions of
the equations are possible, and these are only partly concordant
with observations.
This prediction was verified experimentally within a few years by the American physicists Clinton Joseph Davisson and Lester Halbert Germer and the British physicist George Paget Thomson.
They showed
that a beam of electrons scattered by a crystal produces a
diffraction pattern characteristic of a wave (see Diffraction). The
wave concept of a particle led the Austrian physicist Erwin
Schrödinger to develop a so-called wave equation to describe the
wave properties of a particle and, more specifically, the wave
behavior of the electron in the hydrogen atom.
The Schrödinger wave equation thus had only certain discrete solutions; these solutions were mathematical expressions in which quantum numbers appeared as parameters. (Quantum numbers are integers developed in particle physics to give the magnitudes of certain characteristic quantities of particles or systems.)
The Schrödinger equation was solved for the hydrogen atom and gave conclusions in substantial agreement with earlier quantum theory. Moreover, it was solvable for the helium atom, which earlier theory had failed to explain adequately, and here also it was in agreement with experimental evidence. The solutions of the Schrödinger equation also indicated that no two electrons could have the same four quantum numbers - that is, be in the same energy state.
This
rule, which had already been established empirically by
Austro-American physicist and Nobel laureate Wolfgang Pauli in 1925,
is called the exclusion principle.
Austrian physicist and Nobel Prize
winner Erwin Schrödinger discussed this apparent paradox in a
lecture in Geneva, Switzerland, in 1952. A condensed and translated
version of his lecture appeared in Scientific American the following
year.
Today a physicist no longer can distinguish significantly between
matter and something else. We no longer contrast matter with forces
or fields of force as different entities; we know now that these
concepts must be merged. It is true that we speak of "empty" space
(i.e., space free of matter), but space is never really empty,
because even in the remotest voids of the universe there is always
starlight - and that is matter. Besides, space is filled with
gravitational fields, and according to Einstein gravity and inertia
cannot very well be separated.
Physics stands at a grave crisis of
ideas. In the face of this crisis, many maintain that no objective
picture of reality is possible. However, the optimists among us (of
whom I consider myself one) look upon this view as a philosophical
extravagance born of despair. We hope that the present fluctuations
of thinking are only indications of an upheaval of old beliefs which
in the end will lead to something better than the mess of formulas
which today surrounds our subject.
Like Cervantes' tale of Sancho Panza, who loses his donkey in one chapter but a few chapters
later, thanks to the forgetfulness of the author, is riding the dear
little animal again, our story has contradictions. We must start
with the well-established concept that matter is composed of
corpuscles or atoms, whose existence has been quite "tangibly"
demonstrated by many beautiful experiments, and with Max Planck's
discovery that energy also comes in indivisible units, called
quanta, which are supposed to be transferred abruptly from one
carrier to another.
Discreteness
arises merely as a structure from the laws governing the phenomena.
These laws are by no means fully understood; a probably correct
analogue from the physics of palpable bodies is the way various
partial tones of a bell derive from its shape and from the laws of
elasticity to which, of themselves, nothing discontinuous adheres.
The
concept of atoms and molecules in violent motion, colliding and
rebounding again and again, led to full comprehension of all the
properties of gases: their elastic and thermal properties, their
viscosity, heat conductivity and diffusion. At the same time it led
to a firm foundation of the mechanical theory of heat, namely, that
heat is the motion of these ultimate particles, which becomes
increasingly violent with rising temperature.
The
mass of a nucleus is less than the sum of the masses of its
component particles; the lost mass becomes the binding energy
holding the nucleus firmly together. This is called the packing
effect. The nuclear forces of course are not electrical forces - those
are repellent - but are much stronger and act only within very short
distances, about 10-13 centimeter.
Everything has the continuous structure with which we are familiar
in fields, as well as the discrete structure with which we are
equally familiar in particles. This concept is supported by
innumerable experimental facts and is accepted in general, though
opinions differ on details, as we shall see.
The difficulty of combining these two so very different character
traits in one mental picture is the main stumbling-block that causes
our conception of matter to be so uncertain.
It is true that one cannot kill anybody
with one such racing particle, or else we should all be dead by now.
But their study promises, indirectly, a hastened realization of the
plan for the annihilation of mankind which is so close to all our
hearts.
A
specific device for detecting and recording single particles is the
Geiger-Müller counter. In this short résumé I cannot possibly
exhaust the many ways in which we can observe single particles.
Light impinging from one direction is scattered by them and collected in different directions depending on its wavelength. But even the finest ruled gratings we can produce are too coarse to scatter the very much shorter waves associated with matter. The fine lattices of crystals, however, which Max von Laue first used as gratings to analyze the very short X-rays, will do the same for "matter waves."
Directed at the surface of a crystal, high-velocity
streams of particles manifest their wave nature. With crystal
gratings physicists have diffracted and measured the wavelengths of
electrons, neutrons and protons.
This was extremely startling, because up to that time energy had been a highly abstract concept. Five years later Einstein told us that energy has mass and mass is energy; in other words, that they are one and the same. Now the scales begin to fall from our eyes: our dear old atoms, corpuscles, particles are Planck's energy quanta. The carriers of those quanta are themselves quanta. One gets dizzy.
Something quite fundamental must lie at the bottom of this,
but it is not surprising that the secret is not yet understood.
After all, the scales did not fall suddenly. It took 20 or 30 years.
And perhaps they still have not fallen completely.
By an ingenious and appropriate generalization of Planck's hypothesis Niels Bohr taught us to understand the line spectra of atoms and molecules and how atoms were composed of heavy, positively charged nuclei with light, negatively charged electrons revolving around them.
Each small system - atom or molecule - can harbor only definite discrete energy quantities, corresponding to its nature or its constitution. In transition from a higher to a lower "energy level" it emits the excess energy as a radiation quantum of definite wavelength, inversely proportional to the quantum given off.
This
means that a quantum of given magnitude manifests itself in a
periodic process of definite frequency which is directly
proportional to the quantum; the frequency equals the energy quantum
divided by the famous Planck's constant, h.
The particle for which he postulated such a wave was the electron. Within two years the "electron waves" required by his theory were demonstrated by the famous electron diffraction experiment of C. J. Davisson and L. H. Germer.
This was the starting
point for the cognition that everything - anything at all - is
simultaneously particle and wave field. Thus de Broglie's
dissertation initiated our uncertainty about the nature of matter.
Both the particle picture and the wave picture have truth value, and
we cannot give up either one or the other. But we do not know how to
combine them.
These lines are known as the wave "normals" or "rays."
For one thing, it is, after all, somewhat vague, the more so the greater the wavelength.
For another, quite
often we are dealing not with a small packet but with an extended
wave. For still another, we must also deal with the important
special case of very small "packelets" which form a kind of
"standing wave" which can have no wave fronts or wave normals.
However, these concepts of
longitudinal and transversal structures are not sharply defined and
absolute, since the concepts of wave front and wave normal are not,
either.
The water waves in the basin are an analogue of a wave phenomenon associated with electrons, which occurs in a region just about the size of the atom. The normal frequencies of the wave group washing around the atomic nucleus are universally found to be exactly equal to Bohr's atomic "energy levels" divided by Planck's constant h.
Thus the ingenious yet somewhat artificial assumptions of Bohr's model of the atom, as well as of the older quantum theory in general, are superseded by the far more natural idea of de Broglie's wave phenomenon.
The wave
phenomenon forms the "body" proper of the atom. It takes the place
of the individual pointlike electrons which in Bohr's model are
supposed to swarm around the nucleus. Such pointlike single
particles are completely out of the question within the atom, and if
one still thinks of the nucleus itself in this way one does so quite
consciously for reasons of expediency.
Yet we have seen that because of the identity of mass
and energy, we must consider the particles themselves as Planck's
energy quanta. This is at first frightening. For the substituted
theory implies that we can no longer consider the individual
particle as a well-defined permanent entity.
Another conclusive reason for not attributing identifiable sameness to individual particles is that we must obliterate their individualities whenever we consider two or more interacting particles of the same kind, e.g., the two electrons of a helium atom. Two situations which are distinguished only by the interchange of the two electrons must be counted as one and the same; if they are counted as two equal situations, nonsense obtains.
This circumstance holds for any kind of particle in arbitrary
numbers without exception.
For instance, an important word in the standing vocabulary of quantum theory is "probability," referring to transition from one level to another. But, after all, one can speak of the probability of an event only assuming that, occasionally, it actually occurs. If it does occur, the transition must indeed be sudden, since intermediate stages are disclaimed.
Moreover, if it takes time, it
might conceivably be interrupted halfway by an unforeseen
disturbance. This possibility leaves one completely at sea.
But once one deprives the waves
of reality and assigns them only a kind of informative role, it
becomes very difficult to understand the phenomena of interference
and diffraction on the basis of the combined action of discrete
single particles. It certainly seems easier to explain particle
tracks in terms of waves than to explain the wave phenomenon in
terms of corpuscles.
Therefore I want to recall something else. I spoke of a corpuscle's not being an individual. Properly speaking, one never observes the same particle a second time - very much as Heraclitus says of the river. You cannot mark an electron, you cannot paint it red. Indeed, you must not even think of it as marked; if you do, your "counting" will be false and you will get wrong results at every step - for the structure of line spectra, in thermodynamics and elsewhere.
A wave, on the other hand, can easily be imprinted with an individual structure by which it can be recognized beyond doubt. Think of the beacon fires that guide ships at sea.
The light shines according to a definite code; for example: three seconds light, five seconds dark, one second light, another pause of five seconds, and again light for three seconds - the skipper knows that is San Sebastian. Or you talk by wireless telephone with a friend across the Atlantic; as soon as he says, "Hello there, Edward Meier speaking," you know that his voice has imprinted on the radio wave a structure which can be distinguished from any other.
But one does not have to go that far. If your wife
calls, "Francis!" from the garden, it is exactly the same thing,
except that the structure is printed on sound waves and the trip is
shorter (though it takes somewhat longer than the journey of radio
waves across the Atlantic). All our verbal communication is based on
imprinted individual wave structures. And, according to the same
principle, what a wealth of details is transmitted to us in rapid
succession by the movie or the television picture!
But when you attempt to apply certain somewhat involved enumerations to the gas, you must carry them out in different ways according to the mental picture with which you approach it. If you treat the gas as consisting of particles, then no individuality must be ascribed to them, as I said. If, however, you concentrate on the matter wave trains instead of on the particles, every one of the wave trains has a well-defined structure which is different from that of any other.
It is true that there are many pairs of waves which are so similar
to each other that they could change roles without any noticeable
effect on the gas. But if you should count the very many similar
states formed in this way as merely a single one, the result would
be quite wrong.
This view is so much more convenient than the
roundabout consideration of wave trains that we cannot do without
it, just as the chemist does not discard his valence-bond formulas,
although he fully realizes that they represent a drastic
simplification of a rather involved wave-mechanical situation.
At the most, it may be permissible to say that one can think of particles as more or less temporary entities within the wave field whose form and general behavior are nevertheless so clearly and sharply determined by the laws of waves that many processes take place as if these temporary entities were substantial permanent beings.
The mass and the charge of particles, defined with such precision, must then be counted among the structural elements determined by the wave laws.
The conservation of charge and mass in
the large must be considered as a statistical effect, based on the
"law of large numbers."
According to Heisenberg's theory, which was developed in collaboration with the German physicists Max Born and Ernst Pascual Jordan, the formula was not a differential equation but a matrix: an array consisting of an infinite number of rows, each row consisting of an infinite number of quantities.
Matrix mechanics introduced infinite matrices to represent the position and momentum of an electron inside an atom. Also, different matrices exist, one for each observable physical property associated with the motion of an electron, such as energy, position, momentum, and angular momentum.
These matrices, like Schrödinger's differential equations, could be solved; in other words, they could be manipulated to produce predictions as to the frequencies of the lines in the hydrogen spectrum and other observable quantities.
Like wave mechanics,
matrix mechanics was in agreement with the earlier quantum theory
for processes in which the earlier quantum theory agreed with
experiment; it was also useful in explaining phenomena that earlier
quantum theory could not explain.
Even for the simple hydrogen atom, which consists of two particles, both mathematical interpretations are extremely complex. The next simplest atom, helium, has three particles, and even in the relatively simple mathematics of classical dynamics, the three-body problem (that of describing the mutual interactions of three separate bodies) is not entirely soluble.
The energy levels can be calculated accurately,
however, even if not exactly. In applying quantum-mechanics
mathematics to relatively complex situations, a physicist can use
one of a number of mathematical formulations. The choice depends on
the convenience of the formulation for obtaining suitable
approximate solutions.
Surrounding the nucleus is a series of stationary waves; these waves have crests at certain points, each complete standing wave representing an orbit. The absolute square of the amplitude of the wave at any point is a measure of the probability that an electron will be found at that point at any given time.
Thus, an electron can
no longer be said to be at any precise point at any given time.
This principle states the impossibility of simultaneously specifying the precise position and momentum of any particle. In other words, the more accurately a particle's momentum is measured and known, the less accuracy there can be in the measurement and knowledge of its position.
This principle is also fundamental to the
understanding of quantum mechanics as it is generally accepted
today: The wave and particle character of electromagnetic radiation
can be understood as two complementary properties of radiation.
At a low enough temperature this wavelength is predicted to exceed the spacing between particles, causing atoms to overlap, becoming indistinguishable, and melding into a single quantum state.
In 1995 a team of Colorado scientists, led by National Institutes of Standards and Technology physicist Eric Cornell and University of Colorado physicist Carl Weiman, cooled rubidium atoms to a temperature so low that the particles entered this merged state, known as a Bose-Einstein condensate.
The condensate essentially
behaves like one atom even though it is made up of thousands.
Physicists Condense Supercooled Atoms, Forming New State of Matter
This phenomenon was first predicted
about 70 years ago by the theories of German-born American physicist
Albert Einstein and Indian physicist Satyendra Nath Bose. The
condensed particles are considered a new state of matter, different
from the common states of matter - gas, liquid, and solid - and from
plasma, a high temperature, ionized form of matter that is found in
the sun and other stars.
The effort began when methods of cooling and trapping became refined
enough that it seemed possible to reach the required conditions of
temperature and density.
One unusual characteristic of the condensate is that it is composed of atoms that have lost their individual identities. This is analogous to laser light, which is composed of light particles, or photons, that similarly have become indistinguishable and all behave in exactly the same manner. The laser has found a myriad of uses both in practical applications and in theoretical research, and the Bose-Einstein condensate may turn out to be just as important.
Some
scientists speculate that if a condensate can be readily produced
and sustained, it could be used to miniaturize and speed up computer
components to a scale and quickness not possible before.
Those two groups of particles
behave according to different sets of statistical rules. Bosons have
spins that are a constant number multiplied by an integer (e.g., 0,
1, 2, 3). Fermions have spins that are that same constant multiplied
by an odd half-integer (1/2, 3/2, 5/2, etc.). Examples of fermions
are the protons and neutrons that make up an atom's nucleus, and
electrons.
For instance, an isotope of helium called helium-4 turns out to be a bose particle. Helium-4 is made up of six fermi particles: two electrons orbiting a nucleus made up of two protons and two neutrons.
Adding up six odd half-integers will yield
a whole integer, making helium-4 a boson. The atoms of rubidium used
in the Colorado experiment are bose particles as well. Only bose
atoms may form a condensate, but they do so only at a sufficiently
low temperature and high density.
The slower the
particles, the lower their momentum. In essence, the cooling brought
the momentum of the gas particles closer and closer to precisely
zero, as the temperature decreased to within a few billionths of a
degree Kelvin. (Kelvin degrees are on the scale of degrees Celsius,
but zero Kelvin is absolute zero, while zero Celsius is the freezing
point of water.)
Cornell
and Wieman then released the atoms from the "trap" in which they had
been cooling and sent a pulse of laser light at the condensate,
basically blowing it apart. They recorded an image of the expanding
cloud of atoms. Prior to the light pulse, when the density dropped
after the atoms were released, the physicists believed the
temperature of the condensate fell to an amazing frigidity of 20
nanoKelvins (20 billionths of one degree above absolute zero).
This occurs because the
particles in that gas, even if the gas was very cold, were moving in
all different directions with various energies when the gas was
pushed outwards.
Liquid helium-4, which at
very low temperatures is also a superconductor of heat, behaves in
dramatic ways, trickling up the sides of containers and rising in
fountains.
These paired electrons merge into an overall substance that flows freely through the superconductor, offering no resistance to electric current.
Thus, once initiated, a current can flow
indefinitely in a superconductor.
It gradually enhanced the understanding of the structure of matter, and it provided a theoretical basis for the understanding of atomic structure (see Atom and Atomic Theory) and the phenomenon of spectral lines: Each spectral line corresponds to the energy of a photon transmitted or absorbed when an electron makes a transition from one energy level to another.
The understanding of chemical bonding was fundamentally transformed by quantum mechanics and came to be based on Schrödinger's wave equations.
New fields in physics
emerged - condensed matter physics, superconductivity, nuclear
physics, and elementary particle physics (see Physics) - that all
found a consistent basis in quantum mechanics.
In the years since 1925, no fundamental deficiencies have been found in quantum mechanics, although the question of whether the theory should be accepted as complete has come under discussion.
In the 1930s the application of quantum
mechanics and special relativity to the theory of the electron (see
Quantum Electrodynamics) allowed the British physicist Paul Dirac to
formulate an equation that referred to the existence of the spin of
the electron. It further led to the prediction of the existence of
the positron, which was experimentally verified by the American
physicist Carl David Anderson.
It also led to a grave problem, however, called the divergence difficulty: Certain parameters, such as the so-called bare mass and bare charge of electrons, appear to be infinite in Dirac's equations.
(The terms bare mass and bare charge refer to hypothetical electrons that do not interact with any matter or radiation; in reality, electrons interact with their own electric field.)
This difficulty was partly resolved in 1947-49 in a program called renormalization, developed by the Japanese physicist Shin'ichirô Tomonaga, the American physicists Julian S. Schwinger and Richard Feynman, and the British physicist Freeman Dyson.
In this program, the bare mass and charge of the electron are chosen to be infinite in such a way that other infinite physical quantities are canceled out in the equations.
Renormalization greatly increased
the accuracy with which the structure of atoms could be calculated
from first principles.
Scientists have discovered what Smith refers to as sibling and cousin particles to the electron, but much about the nature of these particles is still a mystery.
One way scientists learn about these particles is to
accelerate them to high energies, smash them together, and then
study what happens when they collide. By observing the behavior of
these particles, scientists hope to learn more about the fundamental
structures of the universe.
In the intervening years we
have come to understand the mechanics that describe the behavior of
electrons - and indeed of all matter on a small scale - which is called
quantum mechanics. By exploiting this knowledge, we have learned to
manipulate electrons and make devices of a tremendous practical and
economic importance, such as transistors and lasers.
The mu and the tau seem to be
identical copies of the electron, except that they are respectively
200 and 3,500 times heavier. Their role in the scheme of things and
the origin of their different masses remain mysteries - just the sort
of mysteries that particle physicists, who study the constituents of
matter and the forces that control their behavior, wish to resolve.
We now know that all these particles are made of more elementary entities, called quarks. In a collision, pairs of quarks and their antiparticles, called antiquarks, can be created: part of the energy (e) of the incoming particles is turned into mass (m) of these new particles, thanks to the famous equivalence e = mc2.
The quarks in the projectiles and the created
quark-antiquark pairs can then rearrange themselves to make various
different sorts of new particles.
On paper,
a possible mechanism is known, called the Higgs mechanism, after the
British physicist Peter Higgs who invented it. But there are
alternative mechanisms, and in any case the Higgs mechanism is a
generic idea. We not only need to know if nature uses it, but if so,
how it is realized in detail.
By studying what happens in the collisions of these particles, which are typically electrons or protons (the nuclei of hydrogen atoms), we can learn about their natures. The conditions that are created in these collisions of particles existed just after the birth of the universe, when it was extremely hot and dense.
Knowledge derived
from experiments in particle physics is therefore essential input
for those who wish to understand the structure of the universe as a
whole, and how it evolved from an initial fireball into its present
form.
If this is so, the electron and the other known particles
will continue forever to appear to be fundamental pointlike objects,
even if the - currently very speculative - "string theory" scores enough
successes to convince us that this is not the case!
Quantum mechanics underlies current attempts to account for the strong nuclear force and to develop a unified theory for all the fundamental interactions of matter.
Nevertheless, doubts exist about the completeness of quantum theory. The divergence difficulty, for example, is only partly resolved. Just as Newtonian mechanics was eventually amended by quantum mechanics and relativity, many scientists - and Einstein was among them - are convinced that quantum theory will also undergo profound changes in the future.
Great theoretical difficulties exist, for example, between quantum mechanics and chaos theory, which began to develop rapidly in the 1980s.
Ongoing efforts are being made by
theorists such as the British physicist Stephen Hawking, to develop
a system that encompasses both relativity and quantum mechanics.
Quantum computers under development use components of a chloroform molecule (a combination of chlorine and hydrogen atoms) and a variation of a medical procedure called magnetic resonance imaging (MRI) to compute at a molecular level. Scientists used a branch of physics called quantum mechanics, which describes the activity of subatomic particles (particles that make up atoms), as the basis for quantum computing.
Quantum computers may one day be thousands to millions of times faster than current computers, because they take advantage of the laws that govern the behavior of subatomic particles. These laws allow quantum computers to examine all possible answers to a query at one time.
Future uses of quantum
computers could include code breaking and large database queries.
Raymond Laflamme, of
the Los Alamos National Laboratory in New Mexico, has carried out a
new calculation which suggests that the Universe cannot start out
uniform, go through a cycle of expansion and collapse, and end up in
a uniform state. It could start out disordered, expand, and then
collapse back into disorder. But, since the COBE data show that our
Universe was born in a smooth and uniform state, this symmetric
possibility cannot be applied to the real Universe.
There, the arrow of time is linked to the so-called "collapse of the wave function", which happens, for example, when an electron wave moving through a TV tube collapses into a point particle on the screen of the TV.
Some researchers have tried to make the quantum
description of reality symmetric in time, by including both the
original state of the system (the TV tube before the electron passes
through) and the final state (the TV tube after the electron has
passed through) in one mathematical description.
He
has found time-asymmetric solutions to the equations - but only if
both Big Bang and Big Crunch are highly disordered, with the
Universe more ordered in the middle of its life.
The implication
is that even if the present expansion of the Universe does reverse,
time will not run backwards and broken cups will not start re-
assembling themselves. |
Quantum Theory, also quantum mechanics, in physics, a theory based
on using the concept of the quantum unit to describe the dynamic
properties of subatomic particles and the interactions of matter and
radiation.