ANCIENT EGYPTIAN GEODESY
The diagonal line from Memphis to Abu Roash extends to Alexandria on the northwestern edge of the Nile delta. Just as this line from Alexandria to Giza is 51.85° south of due east, the line from Port Said to Giza is 51.85° south of due west. The Port Said-Alexandria-Giza triangle has the same angular dimensions as the Great Pyramid.
The base lengths of the Great Pyramid are 440 cubits. The height is 280 cubits and the apothem (the slant height of the faces) is 356 cubits. Converted to miles, the base length is .143 miles and the slant height is .116 miles. The distance from Giza to the Port of Alexandria is just under 116 miles and the distance from Giza to Port Said is also just under 116 miles. The distance from Port Said to Alexandria is just under 143 miles. The triangle inscribing the Delta in the illustration below has the same angular dimensions and is precisely 1,000 times larger than the Great Pyramid.
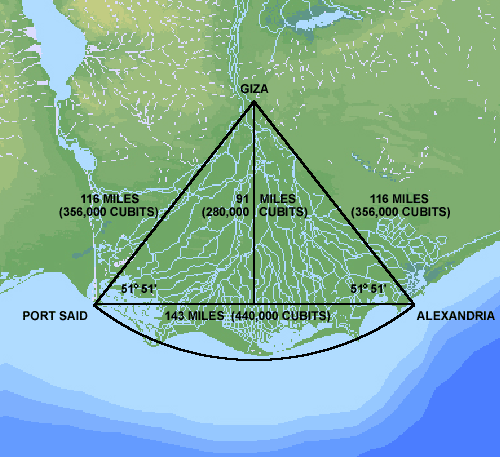
The apex of the triangle is located at Giza and the two corners are a couple of miles beyond Port Said and Alexandria. As shown by the bathymetric image, the Mediterranean Sea is very shallow just beyond the delta. Prior to the final meltdown from the last Ice Age approximately 7,500 years ago, the corners of this triangle were above sea level.
Underwater ruins have recently been discovered in the immediate vicinity of the northwest corner, just outside the Port of Alexandria. All of the points along the arc in the diagram are 116 miles from Giza, 1,000 times the length of the apothem of the Great Pyramid. Textual evidence from ancient Egyptian sources refers to a predynastic capital city known as Behdet, located near the shoreline in the middle of the delta. This city has not been found in modern times and may also be located just beyond the shoreline, 116 miles from Giza.
The length of the apothem of the Great Pyramid and the length of the sides of the triangle that inscribe the delta are also precise measures of the circumference of the earth, in relation to the precession of the equinoxes. One full cycle of precession takes 25,776 years. The average length of each of the 12 astronomical ages is 2,148 years:
25,776 years ÷ 12 = 2,148 years
356 cubits converts to 611.73 feet and this converts to .11586 miles:
356 cubits x 20.62 ÷ 12 = 611.73 feet
611.73 feet ÷ 5,280 = .11586 miles
.11586 miles x 2,14800 = 24,887 miles
356,000 cubits converts to 115.86 miles.
115.86 miles x 214.8 = 24,887 miles
24,887 miles is a precise expression of the circumference of the earth.
Alexandria is located at 30° 00' east longitude and Port Said is located at 32° 19' east longitude. Halfway between the two, the Great pyramid is located at 31° 09' east longitude. The longitude of the Great pyramid was regarded as the prime meridian in the remote past. More recently, the rose line that runs through Paris, France was regarded as the prime meridian and presently the longitude of Greenwich, England is regarded as the prime meridian. Paris is located at 2° 19' east longitude. Just as 2° 19' of longitude separates Alexandria from Port Said, 2° 19' of longitude also separates Greenwich from Paris.
In 2003 Dave Parker found that the ancient Egyptian monumental centers at Giza, Amarna, Luxor and Philae are all at significant latitudes in relation to the circumference of the earth. Parker subsequently learned that Dennis Rawlins had made this same finding some years earlier. Unit fractions such as ½, ¼, etc., are known to have been a favored method of calculation in ancient Egypt. The distance from the equator to the 30th parallel is one-third of the 90° distance from the equator to the north pole. The distance from the equator to the 30th parallel is also one-twelfth of the 360° circumference of the earth. Giza is just over one mile south of the 30th parallel.
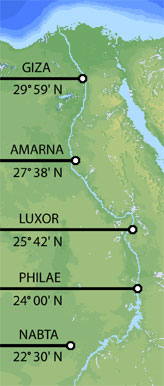
Around 1,350 B.C. Pharoah Akhenaten moved the capital of ancient Egypt from Luxor to Amarna. The ruins of Amarna extend approximately eight miles NS along the Nile. Ancient Egyptian texts indicate that the northern and southern boundaries of the city were carefully marked by boundary stelae but no trace of these boundary stelae has been found in modern times. The ancient capital city at Amarna was centered on 27° 38' N. The northern boundary of the city would have been close to to 27° 41' N The distance from 27° 41' N to the equator is one-thirteenth of the circumference of the earth:
360° ÷ 13 = 27° 41'
Luxor (Thebes) became the capitol of ancient Egypt after Memphis and remained an important monumental city throughout dynastic Egypt. Located at 25° 42' N, the distance from Luxor to the equator is one-fourteenth of the circumference of the earth:
360° ÷ 14 = 25° 42'
The traditional southern border of dynastic Egypt was marked by the first cataract of the Nile and the monumental city of Philae, at 24° 00' N. The distance from Philae to the equator is one-fifteenth of the circumference of the earth:
360° ÷ 15 = 24° 00'
At Nabta Playa, astronomically aligned megalithic stone circles have been dated to 4,000 B.C. Located at 22° 30' N, the distance from the equator to Nabta is ¼ of the distance from the equator to the north pole. The distance from the equator to Nabta is is also one-sixteenth of the circumference of the earth:
90° ÷ 4 = 22° 30'
360° ÷ 16 = 22° 30'
Giza is six degrees north of Philae. Six degrees is 1/15th of the distance from the equator to the north pole. Six degrees is also 1/60th of the circumference of the earth:
90° ÷ 15 = 6°
360° ÷ 60 = 6°
Eratosthenes was born in Cyrene (now Shahhat, Libya) around 276 B.C. and after studying in Alexandria and Athens he became the third director of the Library of Alexandria. He is presently referred to as the father of geodesic science and the first man to measure the earth, but in his own day his nickname was Beta, which means second. Eratosthenes' works have been lost although the titles of his major works have come down to us from secondary sources, such as his treatise On the Measurement of the Earth.
Eratosthenes heard (or read) that at noon on the summer solstice the sun shined directly into a deep well near the southern border of ancient Egypt in the city of Syene, marking the latitude of Syene as the Tropic of Cancer. Eratosthenes reported that Syene and the Tropic of Cancer were located at 23° 51' north latitude. He also reported that in Alexandria at noon on the summer solstice the sun cast a shadow with an angle of 7° 12'. This led Eratosthenes to believe that Alexandria was 7° 12' north of Syene, at 31° 03' north latitude. Eratosthenes understood that 7° 12' is 1/50th of 360°, thus 1/50th of the circumference of the earth, so he concluded that the distance from Syene to Alexandria was 1/50th of the circumference of the earth.
Eratosthenes reported that Syene was due south of Alexandria on the same meridian, and he reported that the distance from Syene to Alexandria was 5,000 stadia. The stadia that Eratosthenes referred to is in dispute. The most widespread view is that he was referring to a Greco/Roman stadia of 600 Roman feet. This stadia times 5,000 times 50 is about 15% longer than the actual circumference of the earth, which most commentators regard as a good estimate for Eratosthenes' day.
Syene is actually located at 24° 06' north latitude. The Tropic of Cancer was located at 23° 51' north latitude during the dynastic period of ancient Egypt, but by the time of Eratosthenes the tropic had moved down to 23° 45' north latitude. The sun shines directly down on an area of the earth covering one-half of one degree of latitude. When the Tropic of Cancer was at 23° 51' N, the northern edge of the sun at noon on the summer solstice would have shined directly down into the well at Syene, one-quarter of one degree north of the Tropic of Cancer. In Eratosthenes' day, the tropic had moved too far south for the sun to shine directly down into the well at Syene.
Alexandria is actually located at 31° 12' north latitude. Since the tropic was at 23° 45' north latitude in Eratosthenes' day and since the northern edge of direct downward sunlight is an additional one-quarter of one degree north, the northern edge of direct downward sunlight on the summer solstice in Eratosthenes' day would have been at 24° 00' north latitude and the angle of the shadow cast by the northern edge of the sun at noon on the summer solstice in Alexandria would have been 7° 12', just as Eratosthenes reported.
Syene is actually almost three full degrees of longitude east of Alexandria The distance from Syene to Alexandria is not 5,000 stadia regardless of what stadia is employed, because Syene is so far east of Alexandria. The reason Eratosthenes got the latitude for Alexandria wrong was because he was basing the difference on an incorrect assumption about the latitude of Syene, an incorrect assumption about the latitude of the tropic and because he was unaware that the sun shines directly down on an area one-quarte of one degree north of the tropic.
Although the distance from Alexandria to Syene is not equal to 1/50th of the circumference of the earth, the distance from the latitude of Alexandria to the latitude of Philae, six minutes south of Syene at the southern border of ancient Egypt, is equal to 1/50th of the circumference of the earth (7° 12'). According to Livio Stecchini, the ancient Egyptians employed a stadia of 300 cubits, although this measure was not in use during Eratosthenes' day. The ancient Egyptian cubit of 20.62 inches, times 300, times 5,000 equals 488 miles. The distance due north-south from the latitude of Alexandria to the latitude of Syene is 488 miles.
Modern scholars say it is a happy coincidence that all of Eratosthenes' errors tended to cancel out, resulting in a fairly accurate measure of the circumference of the earth, even though most of his data and calculations were wrong. All of this suggests that Eratosthenes did not stray too far from accurate conclusions because he already knew from fragmentary records in the Library of Alexandria that the boundaries of ancient Egypt had originally been set at 1/50th of the circumference of the earth and that the distance from the latitude of Alexandria to the latitude of Syene was 1,500,000 cubits or 5,000 ancient Egyptian stadia. If Eratosthenes acknowledged this, it could explain the loss of all of his works even though other Greek works from before, during and after his time have survived.

Although the city of Akhenaten at Amarna was already in ruins by the time of Eratosthenes, modern excavations indicate that the southern boundary of Amarna was close to 27° 36' north latitude, precisely half-way between the latitude of Alexandria and the latitude of the southern border of ancient Egypt at Philae. The southern boundary of Amarna is 3.6° south of Alexandria, precisely 1/100th (one percent) of the 360° circumference of the earth. The southern boundary of Amarna is 3.6° north of Philae, also precisely 1/100th (one percent) of the 360° circumference of the earth.
Written around 440 B.C., chapter two of The Histories of Herodotus contains the following statement:
"From Heliopolis to Thebes is nine days' sail up the river; the distance is eighty-one schoenes, or 4860 furlongs. If we now put together the several measurements of the country we shall find that the distance along shore is, as I stated above, 3600 furlongs, and the distance from the sea inland to Thebes 6120 furlongs. Further, it is a distance of eighteen hundred furlongs from Thebes to the place called Elephantine."
Located in the middle of the Nile, Elephantine Island was a part of the ancient city of Syene. The deep well at Syene that Eratosthenes mentions is on Elephantine Island. 6120 furlongs from the sea to Thebes, plus 1800 furlongs from Thebes to Elephantine, equals 7920 furlongs from the southern border of Egypt to the sea. This is the same number as the measure of the diameter of the earth in English miles.
The length of the ancient Egyptian schoene was 12,000 cubits. Herodotus says that 81 schoenes is equal to 4860 furlongs. This is a ratio of 60:1. 1/60th of 12,000 cubits is 200 cubits, or 300 ancient Egyptian feet, for the furlong used by Herodotus. At 20.62 inches or 1.7183333 English feet per cubit, 200 cubits is 343.6666 English feet. 7920 of these furlongs is 2,721,840 English feet, or 515.5 miles. The distance, due north-south, from the northern coast of the delta at 31° 33' N, to the latitude of Syene/Elephantine ( 24° 6' N), is also 515.5 miles. However, the distance along the Nile from the northern shore of Egypt to Elephantine is much longer because of the twists and turns of the Nile. Even as the crow flies, the distance from the northern edge of the delta to Elephantine is considerably longer because Elephantine is about two degrees further east than the northernmost point of the delta.
In the modern era, the ability to accurately measure long distances along the same longitude only became possible with the advent of accurate chronometers in the 18th century A.D. It would have been impossible for Herodotus to accurately measure the length of Egypt from north to south, along the same longitude, by sailing up the Nile as he suggests. Like Eratosthenes, the accuracy of Herodotus' report suggests that his information came from older and more advanced sources.