|
Part One: So what is a Diamagnetic Vortex, Anyway?
Since we have been looking at Dr. Richard Lefors Clarkís "bowtie"
shaped
vortices in great detail, it is important for us at this point to make
mention of Dr. Clarkís theories of diamagnetism and magnetic null zones.
After all, the Wilcock reading in Chapter 17 suggested that these energy
forces had a lot to do with the siting of ancient monuments. This was given
as the "answer" that would rectify the positioning of certain stone and
earthworks in Munckís system with a mappable, planet-wide grid system.
According to Dr. Clark, the newest advances in the science of magnetism have
shown that there is a positive / negative polarity reversal that occurs in
the center of a magnetic field (see below diagram.)
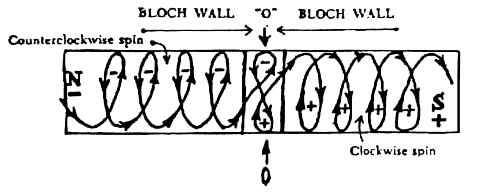
It is at this point, called a "Bloch Wall," where the spiraling energies of
the north pole meet the spiraling energies of the south pole, and they
overlap. At the overlap point, we get the "bowtie" shape that we see on
Earth in the above examples. The point of magnetic flow reversal, or the
"Bloch Wall," creates what we now term as anti-gravity, nulling its effects
and / or changing its direction. Dr. Clark shows in Anti-Gravity and the
World Grid how magnetic scientists have actually studied and measured this
"Bloch Wall" phenomenon using electromagnets.
As we look at the above illustration, we should keep in mind that the lines
on
the Global Grid provide the organization for these spinning magnetic
fields. In other words, the lines on the Grid are flowing like rivers, due
to the spiraling nature of the energies that make them up. And thus, if we
look back to the diagram of the
Bermuda Triangle vortex, we can see that the
north-south vertical line that intersects Grid Point 18 next to Florida
would be the "organizer" for the magnetic energy flows. Then, the magnetic
polarity will reverse at the exact center of the bow-shaped area. It is here
that we will get our "Bloch Wall" effect produced, then causing the
Bermuda
Triangle anomalies, as well as providing exceptional spiritual energy. It is
no surprise that many people will want to go to Florida to retire - the
youthful energy explodes in abundance there!
If it were truly possible that the Earthís magnetic field could produce such
spirals of energy, then we should expect there to be places where it would
be very evidential that something anomalous was occurring. Certainly
Sandersonís work on the "vile vortices" like the Bermuda Triangle satisfies
this, as does Munckís mention of the anomalies surrounding Rock Lake in
Wisconsin. There is another area that also obviously falls under this
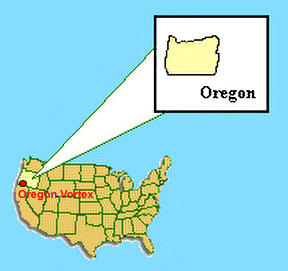
effect, and that is the area known as the Oregon Vortex.
William Childress featured the Oregon Vortex in an article for the
industrial newsmagazine "Compressed Air," which has been circulating in
print for over 100 years. As this is a reputable, mainstream scientific
journal, it would be unlikely for them to print a study that was considered
to be "fringe" science. Instead, it appears that their investigation of this
vortex came from a genuine interest in trying to uncover and understand
anomalous Earth phenomena.
 Childressí article starts out by describing the most crowd-pleasing feature
in the Oregon Vortex / House of Mystery. A 100-year old shack was built over
the vortex, and within this shack, a broom is "standing rigidly straight in
the middle of the room, untouched by anyone or anything, as if it were a
spear stuck in the middle of the floor." The record time for the broom to
remain standing, according to those who run the
House of Mystery, is 36
hours! Childressí article starts out by describing the most crowd-pleasing feature
in the Oregon Vortex / House of Mystery. A 100-year old shack was built over
the vortex, and within this shack, a broom is "standing rigidly straight in
the middle of the room, untouched by anyone or anything, as if it were a
spear stuck in the middle of the floor." The record time for the broom to
remain standing, according to those who run the
House of Mystery, is 36
hours!
Again, we see the harmonic numbers emerging, this time in the number
of hours involved. In another area of the House of Mystery, a golf ball is
placed at the bottom of a trough, and it will roll uphill when released. On
the "Superman Platform," a person can lean very far forward without falling,
and thus appear to look like Superman in flight.
Other stunts that are demonstrated at the Oregon Vortex include height
discrepancies, where two similarly tall people will walk in opposite
directions and have noticeable and opposite changes in their height. A
similar effect is demonstrated when a long plank is placed across two
seven-foot tall posts; on the south end, the plank appears to be higher by a
good three inches.
According to Childress, "in some way still not
understood, a kind of "gravity warp" appears to make vertical objects taller
or shorter as long as they are in the force field." If we think about this
on a much larger scale, we can visualize the expansion and contraction of
landmasses, producing the structures that we have been examining above.
What is actually most interesting to us is the effects that are reported at
the area called the "Vortex Post." As Childress indicates, "people standing
next to the post tend to sway in a circle like some bottom-weighted toy."
From this piece of information, we can indeed see the spiraling nature of
the gravitational fields at work! Also notable is a passage in Charles Berlitzís
Bermuda Triangle where there were reports cited of mariners
encountering spiraling motions on their compass that became faster or slower
depending on how close they were to the center of the vortex. At these
certain times, the spiraling energy from the vortex was actually stronger
than Magnetic North, and overtook the normal operation of the compass.
It is also interesting that the owners of the
Oregon Vortex / House of
Mystery do not permit video cameras. They did not explain to
Childress why
this was so, only stating that regular cameras were permitted. This falls
perfectly in line with the Rock Lake information from Munck, and shows us
that these vortices repetitively show their effects on electronics. We again
remind the reader of the similar effects demonstrated by the UFOs
in thousands of sighting reports.
And so, with the addition of physical information to back up the
diamagnetism theories of Dr. Richard Lefors Clark, we have to consider that
there is more to the Global Grid than just straight lines. We have pieces of
evidence like the bow-shaped structures of the landmasses indicated above,
and now the spiraling, anomalous gravitational effects that can be seen in
various spots. Although the above diagram of the diamagnetic field was drawn
in two dimensions, Dr. Clark makes careful notice of the fact that these
lines of force are indeed three-dimensional spirals.
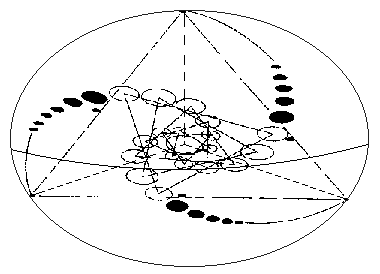
These spirals are very
important to study, as they form the basis for all of the Platonic Solids
that we have spent so much time discussing. And looking in again on the
extended version of the "Triple Julia Set" formation from 1996, this can
clearly be seen:
"click" on above image
Part Two: Simple, Harmonic Relationships
In earlier chapters, we discussed how these universal spirals of energy
generally fall into two main categories; namely, the square root of 2 and
phi. One of our postulates is that Nature, or the physical world that we can
see, will show us all of the secrets in the metaphysical world. Therefore,
these spirals are not only simple mathematical concepts in our own
dimension; they reach their fruition in the functions of the dimensions. Now
that we can see these spirals in action, mapped out for us by the Global
Magnetic Grid and its effect on the shapes of continents, we can explore how
each of the Platonic Solids "fit in" to these spirals.
As is written in Robert Lawlorís book Sacred Geometry, the Platonic Solids
are in a "simple harmonic relationship" to each other. As we can see in
Table II below, that simple relationship is expressed in terms of phi and
the square root of 2 in spiral form. Lawlor gives us a complete breakdown of
the Hindu "spectrum" of shapes, with the harmonic proportions for each one
of them. The measurements listed are comparisons of the length of each side
of the Platonic Solids.
Since every line on any Platonic Solid will be the
same length, these measurements are the universal standard for each shape.
|
1.
|
Sphere
|
[no edges]
|
|
2.
|
Central Icosahedron
|
1 / phi2
|
|
3.
|
Octahedron
|
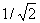
|
|
4.
|
Star Tetrahedron
|
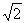
|
|
5.
|
Cube
|
1
|
|
6.
|
Dodecahedron
|
1 / phi
|
|
7.
|
Icosahedron
|
Phi
|
|
8.
|
Sphere
|
[no edges]
|
Table II. Harmonic Proportions of Platonic Solids.
In order for these proportions to be established, the researcher must
determine where the "1" is going to be. We must remember the simple fact
that if you have a square, and each side has a length unit of 1, the
diagonals will measure out to the square root of two. Similarly, if you
assign a unit value of 1 to the diameter of a circle, the circumference will
measure out to pi, or 3.14159 units. In order to compare the Platonic Solids
to each other, we also need to assign a straight value of 1 to the sides of
one of the shapes. In order to have the basic harmonics work out simply and
perfectly, the value of 1 needs to be assigned to the length of the side of
the cube. All other proportions as indicated above represent the exact
numerical value that we receive when comparing their lengths against the
cube.
As we are on the subject of phi, it is also interesting to point out here
that the "solar number" of 666 and the "lunar number" of 1080 also express
the phi ratio when divided into each other. John Michellís work shows how
many ancient monuments used these proportions, and we also see it in nature
as well, being the harmonic relationship between such things as the size of
planets. Since phi seems to be of such penultimate importance, we can see
yet another reason for why the Hindus ascribed such religious significance
to Purusha, or the icosahedron.
Now that we can see the actual mathematical structure of the spiraling
energy that makes up the CU, we no longer need to wonder about whether they
are, in fact, crystallized frequencies. We have seen it on the planetary
level, and now we can see it on a mathematical level as well. Hoaglandís
team made the connection between these geometric shapes and the frequencies
of the dimensions, and many might wonder exactly how he did that. The answer
to that question actually helps us even more in understanding the true
physics behind these harmonic, geometric shapes.
On
his website, Hoagland has printed an early
essay that he composed on hyperdimensional physics back in 1989. In this
essay we have the clearest picture of how the Enterprise Mission team tied
together the physics of higher dimensions with the abstract concept of
Platonic geometry.
The "Message of Cydonia"
First Communication from an Extraterrestrial Civilization?
By
Richard C. Hoagland and Erol O. Torun
Copyright (C) 1989
All Rights Reserved
[We are only going to reprint the part of this article that directly
concerns us here.]
…If in the "Cydonia tetrahedral mathematics" we are truly seeing the
deliberate communication of demonstrable astrophysical effects of a
long-sought "Unified Field Theory," this in itself would be remarkable
confirmation of current efforts to discover such fundamental mathematical
connections between Natureís elemental forces. For, most provocative: one
leading mathematical approach to successfully modeling such connections is
essentially based on a tetrahedral model, and a resulting mathematical
expansion into "higher-dimensional, n-space relationships" (recently
discovered) between the five Platonic solids (Sirag, 1989).
It is very important to note here that
Mr. Saul-Paul Sirag, referenced
below, has referred to ALL of the Platonic Solids in his model of "higher
dimensions," not just the
tetrahedron. The work of Tony Smith also built
upon Siragís geometric models, and a direct reference to Siragís work is
made on
Smithís website.
In particular, these studies relate tetrahedral geometry as being
topologically equivalent to three-toruses -- tori extending into "one more
dimension than our familiar three." [Many current efforts in pursuit of
"unified field models," such as the much-acclaimed "super-string theory,"
routinely involve up to ten mathematical dimensions. Some more recent
theories are exploring twenty-six (Sirag, ibid).]
As we have already stated in previous chapters, by breaking the "symmetry"
of the strings in Superstring Theory, we arrive at an octave-based, 8 or 24
(8 x 3) - dimensional universe. This lines up with Srinivasa Ramanujanís
"modular functions."
Phrased in simple terms:
The routine mathematical representation of vorticular flow in more than
three dimensions -- a three-torus -- by means of three-dimensional
tetrahedral models, opens up the possibility that the demonstrable
geophysical effects of the "Cydonia tetrahedral message"
are attempting to
communicate the reality of additional dimensions (as opposed to mere
mathematical abstractions) -- and the observable reality of vorticular
energy flow between adjoining "n-spaces."
So, if we plug in our own discoveries in this chapter to what
Hoagland and Torun have said here, and use the language that they expressed it with,
Dr.
Clarkís bow-shaped "diamagnetic energy vortices" would be another physical
example of "the observable reality of vorticular energy flow between
adjoining "n-spaces."" Hoaglandís hyperdimensional physics asks us to
visualize the spiraling energies making up the shapes themselves as being
connected together to form a three-torus, which really is nothing more than
what you would see if you removed the tetrahedron from the intersecting,
spiraling lines that formed it. When a number is assigned to a torus as in
this case, it refers to how many visible "sides" the curving line produces.
Thus, a three-torus is essentially like a triangular knot in its appearance.
Such totally unexpected (to non-specialists) and remarkable mathematical
correlations -- between as yet unpublished theoretical work into Unified
Field Models, and the specific tetrahedral geometry apparently intended at
Cydonia -- gives added confidence that such a linkage was in fact intended.
If so, there may be an additional confirmation of such a radical "Cydonia
Unified Field Model"--
In the continuing, puzzling departure of some celestial objects from strict
"Newtonian" mechanics.
And now, we check in on the References section to get a clearer picture on
Mr. Saul-Paul Sirag:
References:
Mr. Saul-Paul Sirag, for furnishing important references linking tetrahedral
mathematics with "two and three-torus topologies," and for providing
examples from his own research of not only Schusterís Hypothesis as
potentially applicable to a Unified Field Model --but for specifically
referencing tetrahedral mathematical topology and the Platonic Solids as
directly applicable; and finally, Mr. Stan Tenen (The Meru Foundation), for
introducing us to Saul-Paul Sirag, for furnishing examples of his own
research into the historical importance of the Platonic Solids (tetrahedra,
in particular), and for valued general discussion of some of the more
controversial aspects of our work.
[Note: Schusterís Hypothesis relates to more recent published material from
The Enterprise Mission regarding the energetic flow between bodies in the
Solar System.]
It is important to point out here that the work of
Stan Tenen, often
referred to by Hoagland, gives us yet another layer of depth to explore in
these matters. Tenen has discovered that the Torah, or the section of the
Old Testament that was apparently dictated to Moses by God, has precisely
encoded the formulae for constructing the Platonic Solids in its passages.
From this same Biblical scripture we also see the bizarre synchronicities
that emerge with apparent mathematical certainty in the work of The Bible
Code, explained in the book by Michael Drosnin of the same title.
(The Bible Code appears to have given us written prophecies of events 2000+
years in the future, in our own modern era. Drosninís biggest "claim to
fame" with the Bible Code was the precise prediction of the assassination of
Israeli Prime Minister Yitzhak Rabin. The perfection of the mathematics
involved in this, and the fact that it does not show up in any other books
of the Bible, has excited mathematicians worldwide. It obviously helps
strengthen the faith of Hebrews in the Torah as well!)
The work of Stan Tenen, showing us the mathematical encoding of the
Platonic
Solids within sacred text, gives us yet another interesting clue as to how
the physical fundamentals of Universal Law and hyperdimensional physics were
preserved as knowledge for us to use by Higher Intelligence. Obviously, Tenenís work is another major area of inquiry, and we leave it up to our
readers to investigate the
Meru Foundation
 The one point that we need to mention here is that
Tenenís work also shows
us a very interesting principle at work in the formation the Hebrew
alphabet. Tenen explains that the Hebrew alphabetical characters represent
different shadows of a single geometric figure. That single geometric figure
is, believe it or not, a spiral shape contained within a tetrahedron! As
amazing as it must seem, all we have to do is rotate the tetrahedron into
different angular positions and then draw the shadows that result. All of
the Hebrew letters will show up in a quite natural progression as a result
of doing this. The one point that we need to mention here is that
Tenenís work also shows
us a very interesting principle at work in the formation the Hebrew
alphabet. Tenen explains that the Hebrew alphabetical characters represent
different shadows of a single geometric figure. That single geometric figure
is, believe it or not, a spiral shape contained within a tetrahedron! As
amazing as it must seem, all we have to do is rotate the tetrahedron into
different angular positions and then draw the shadows that result. All of
the Hebrew letters will show up in a quite natural progression as a result
of doing this.
We remind ourselves that the science of Gematria also started out in the
Hebrew language, giving each of these tetrahedral rotations, or alphabetical
letters, a sequential number. The founders of this science seemed to have
full awareness of the frequency numbers that underlie the dimensions, as
well as their meanings. We remember as one example that 144 was said to
equal Light, and now we can see through the work of Bruce Cathie that
light
speed, in harmonic terms, is indeed 144. And now, we can see that the same
authors of Gematria also knew of the Platonic Solids, as well as the fact
that they have an inner, spiraling nature! The actual structure of the
Hebrew alphabet was intended to show us this.
If we look back to the work of Carl Munck, we can see that the Ancients were
very much concerned with the traditional English inch, foot and mile
measurement when building their sacred sites. The work of John Michell,
which we have not explored in detail here, also shows very significant
relationships of the
Great Pyramid and
Stonehenge to the inch / foot / mile
system. We also remind the reader that the Sumerians gave us the
Constant of
Nineveh, and that it was a value expressed in seconds. We also remind the
reader that the Speed of Light, in conventional terms, is also expressed in
miles per second.
In the chapter on Bruce Cathie, we demonstrated how the harmonic of Light
shows up precisely when we solve the Speed of Light for (x) minutes of arc
per grid second. The value that we end up with is 144,000 minutes of arc per
grid second for the speed of light in free space. This puts it into the
simple harmonic terms that the Universe works off of, and that the minds of
the ETs navigating our globe can understand. Now, we can see here that the
values of miles and seconds are also important in harmonic terms as well, to the Atlanteans and their cohorts. So, we wonder to ourselves, could the
Speed of Light also have harmonic significance when expressed in miles per
second?
We do find that this is indeed the case. Not only that, but it ties in
directly with the science of Gematria, which we have just been re-examining
here. It also ties in with the work of Carl Munck, our pioneer
archeocryptographer who discovered a universal coordinate system being used
within all sacred sites worldwide. It also ties in with the fundamental,
spiraling nature of the geometric forms that the authors of the Gematrian
sciences were very much aware of.
Carl Munck was studying the Gematrian "frequency numbers," and started to
notice that there was a definite mathematical redundancy to them. The
redundancy came when he started calculating the tangents of each number, and
found out that they were all the same! If we remember from trigonometry
class in high school, the tangent function is used to measure the
intersection between a straight line and the very edge of a circle. This
also could obviously be the intersection of a straight line and a curve as
well, thus mapping - you guessed it - a spiral. We now go directly into a
reprint from Mason et al.ís Gematria page, which explains this point, and
eventually tells us how these numbers harmonically tie into the Speed of
Light, measured in miles per second. Here is Mason et al. to explain.
Carl figured a certain logic was demanded by these [Gematrian frequency]
numbers, so he arranged them into two separate scales, organizing them by
their tangents, and marking the numbers that came from the ancient systems
with asterisks (*), and filling in the "blanks," with appropriate numbers,
something like this:

+ 3.077683537 72* 252* 432* 612 792
- 3.077683537 108* 288* 468 648* 828


+ 0.726542528 36* 216* 396* 576* 756*
- 0.726542528 144* 324 504 684 864*

In the newsletter, Carl had a longer list of these numbers in vertical
columns. He also drew in sine waves connecting the numbers, which seemed to
be suggested by their logic. He noted the consistent differences between the
various numbers in the top two rows of 36 and 144, such as 108 - 72 = 36 and
252 - 108 = 144. The differences between the bottom rows are 108 and 72,
such as 144 - 36 = 108; and 216 - 144 = 72.
The suggestion of sine waves, Carl said, is very, very obvious. Did the
ancients know about sine waves? Did they have oscilloscopes? Were they
suggesting a certain frequency?
Part Three: A Frequency of Light
Carl was shocked when he multiplied the two Gematrian tangents:
3.077683537 x 0.726542528 = 2.236067977
He knew that 2.236067977 is the square root of five!!!
Thatís the pyramid codex talking!", Carl says. He asks, "Why does the square
root of five answer the sine waves of the Sacred Numbers? What was the
reasoning behind it?… [The reasoning was that] the square root of five is
itself a Tangent; the Tangent of 186234.09485, which is the speed of light
in air!!!
Carl points out that the speed of light in a vacuum is 186282.5894 miles per
second, but when light travels through air, it is slowed down to
186234.09485 miles per second. Enter this speed-of-light-in-air number into
your calculator, and then press the tangent key, to see that it is very
close to the number arrived at by multiplying the two Gematrian tangents…
[Here we remind ourselves that the tangent is a mathematical function that
can be used to map out a spiral. The Speed of Light has a tangent of the
square root of five, and this in turn has a tangent that harmonically
relates to ALL frequency numbers making up the light / sound / geometric
structure of the Octave of dimensions. You simply multiply their two
commonly shared tangents together to get this number.]
Carl concludes:
And there we have it, the reasoning behind the
Sacred Numbers of Gematria,
the same ones preserved in eastern metrology and western calendrical
computing; square roots and tangents - all keyed to the terrestrial speed of
light - and delivered through the pyramid codex in nearly the exact
methodology they used in keying the earthís equatorial circumference to the
cube root of double-pi when they built the Great Pyramid at Giza.
Munckís work quite well explains how the Great Pyramid was built to unify
the Earthís circumference at the equator with the "constant" of the cube
root of double pi, and it is also explained on Mason et al.ís
Gematria page,
from which this was excerpted.
No communications across ancient oceans? No prehistoric writing that makes
any sense? Ignorant stone age progenitors? Iím afraid Iím not buying
anymore, not when I can so easily find this kind of mathematical evidence to
the contrary.
Someone back there had it all; maps of enviable accuracy, a complete
knowledge of every inch of our planet, a thorough understanding of
mathematics and, yes, even calculators and computers we take for granted
today - because without such tools, they could never have put it all
together. Why do I say that? Because the U.S. Geological Survey advises me
that they have the only computer in the United States which is programmed to
calculate accurate distances between widely separated points anywhere on the
planet - which means - that before the ancients could have marked out the
pyramid grid system, they required a computer of the same caliber!
And so, from this excerpt, we can see very clearly how
Carl Munck has
discovered a similar harmonic function for the Speed of Light in miles per
second, as Cathie did in his own harmonic system. The most amazing point of
all was not addressed by "The Code Gang" in this article, though, and that
is the centering on the square root of five as being so important. What we
see, when investigating Robert Lawlorís book Sacred Geometry, is that the
internal measurements of all the Platonic Solids are a function of phi,
square root of two, square root of three and square root of five. And so,
the connection is obvious - the hidden mathematical properties of light
reveal that it is traveling in a spiral formation, which is exactly what
Ra
tells us in the Law of One series. These spiraling lines or "superstrings"
in the sea of energy known as the "aether" then form the framework for the
different Platonic Solids.
Remember that we just showed above how the lengths of the sides of the
Platonic Solids can all be expressed in terms of phi and the square root of
two. However, a cube with a side length of 1 will have a diagonal of the
square root of two on each of its faces, and if you draw a diagonal through
the center of the cube between two points, its value is the square root of
3. In addition, when we measure the diameters of these shapes, and their
harmonic relationships, one of the most important ratios of all is indeed
the square root of five.
In Lawlorís words,
The square root of five is the proportion which opens the way for the family
of relationships called the Golden Proportion, [or the phi ratio.]
The
Golden Proportion generates a set of symbols which were used by the Platonic
philosophers as a support for the ideal of divine or universal love. It is
through the Golden Division that we can contemplate the fact that the
Creator planted a regenerative seed which will lift the mortal realms of
duality and confusion back towards the image of God.
So, the connection of the square root of five to
the Platonic Solids is the
fact that the phi ratio grows directly out of it. Now we can see from the
work of Carl Munck that the Speed of Light is also directly a function of
the square root of five, and furthermore that the square root of five is
directly a function of the Gematrian Numbers.
This is the cornerstone that we have been waiting for. We have already
expressed the harmonic link between these "perfect" harmonic numbers for the
vibrations of sound in air. These "perfect" numbers only come about when we
measure them against one second of time as we now have it. If our seconds
were shorter, the harmonic ratios would still be preserved, but they would
not be whole numbers any longer. It appears that the second of time that we
now use from the Sumerians gives us perfectly round numbers for the
vibrations of each note in the Octave. This alone suggests a high level of
scientific knowledge that went into this apparently archaic system of
measurement. That only further strengthens the case for why we will see in
later chapters that they also formulated the Constant of Nineveh,
a number
that allows all planetary orbits to be quickly calculated, as being
expressed by a value in seconds.
It is only with the second that we now use that these frequency numbers are
all round and rational. And, that second of time is a precise harmonic
breakdown of one Earth day of 24 hours of 60 minutes with 60 seconds each.
We know that the Gematrian Numbers are all based on the number 9 as a
foundation. Cathie showed us that if you convert our time units from a ratio
of 8 to a ratio of 9, at 27 "grid hours," then we have a measurement of
"grid seconds" that shows us the harmonic "frequency number"
of 144 as the
Speed of Light in free space. We also see the "frequency numbers" coming out
much clearer in the division of the number of Grid seconds per day.
So, in short, we now have a quite sufficient amount of scientific proof to
show us that the Platonic solids are indeed a function of the mathematical
expansion and contraction of curving superstrings in a spherical energy
field, forming natural shapes such as what Hoagland would refer to as a
"three-torus" when constructing a tetrahedron, for example. This same
information regarding spiraling lines of light was revealed to us by
Ra and
other sources, and now we have gone in and directly seen it mathematically.
These superstrings travel at the speed of Light, and now with the work of
Cathie and Munck we can see how the spirals themselves are functions of
Light. The harmonic frequency numbers, expressed in Gematria, are completely
woven into this "fabric" of space and time.
So, what we essentially have here is a bullet-proof mathematical design that
incorporates all of these various points together. We can see how these
consciousness units function in their "inward coalescing" capacity by their
effects on a planetary energy field. Just as Ra told us that the
consciousness unitsí inward expansion creates gravity, so too do we now see
with the Becker / Hagens grid that gravity demonstrates in a quite literal
fashion how these various Platonic shapes emerge.
The actual lines of force
created by the shapes have a direct effect on the shaping of continental
landmass.
TETRAHEDRAL HARMONICS
Further information has now come our way regarding a direct mathematical
connection between Platonic geometries and the harmonic number sequence. As
we briefly mentioned before, at the end of a MUFON conference in 1997,
Richard Hoagland gave a sneak-preview of unpublished research that revealed
that the orbit of Mars had once been exactly 666 Martian days in length,
which is a clear harmonic number. We already know that the Earthís orbit
could well have been 360 days exactly at some point in the past, and that
this might be one explanation for why we have used 360 degrees in a circle.
So, Enterprise Mission associate Erol Torun decided to see
what would happen
if 666 degrees were used in a circle instead of 360. They already had a
collection of all the significant angle relationships between the various
sections of a tetrahedron circumscribed within a sphere, and with few
exceptions these were decimal-point values. Hoagland revealed that when 666
degrees are used, all of these values become whole numbers!
In the table on the next page, we have demonstrated this with our own
calculations, based on Hoaglandís suggestion. The first column shows the
tetrahedral angles in a 360-degree system, the second column shows what the
exact figure must be to harmonize with a 666-degree system precisely, the
third column shows the value in the 666 system and the fourth column
indicates how "harmonic" the 666 value is.
|
360
|
Harmonic Val.
|
666
|
Y/N
|
|
4.0
|
3.783783783784
|
7
|
Y
|
|
19.5
|
19.45945945946
|
36
|
YYY
|
|
22.5
|
22.70270270271
|
42
|
Y
|
|
34.7
|
34.59459459459
|
64
|
YY
|
|
45.0
|
45.40540540541
|
84
|
YY
|
|
49.6
|
49.72972972973
|
92
|
NNN
|
|
52.0
|
51.89189189189
|
96
|
YYY
|
|
55.3
|
55.13513513514
|
102
|
NNN
|
|
60.0
|
60.0
|
111
|
NN
|
|
69.4
|
69.18918918919
|
128
|
Y
|
|
85.3
|
85.40540540541
|
158
|
NNN
|
|
90.0
|
89.72972972973
|
166
|
NN
|
|
94
|
94.05405405405
|
174
|
N
|
|
184
|
183.7837837838
|
340
|
NA
|
|
As we can see from the chart, the more "Yís" there are, the more harmonic
the number is, and the more Nís there are the more non-harmonic the number
is.
If we look at the column of Yís and Nís, we can see that a clear
waveform is visible. [No information was available on our harmonics chart
regarding the last number, hence the NA.] In order to truly see it well, we
would have to graph the Nís as indicating force points in the opposite
direction. Therefore, it is very interesting for us to see that the true
harmonics of the tetrahedron shape appear to be a combination of very
harmonic numbers and very non-harmonic numbers. In the cases where the Nís
emerge, there are very few numbers that divide into the number itself, and
in the cases with many Yís the numbers are harmonic, meaning that they have
a maximum number of divisors.
Considered together, this information reveals a tremendous amount. We now
have solid mathematical proof from the Enterprise Mission that connects the
angles of one of the main Platonic geometries (and almost certainly the
others as well) to the harmonic number series. Furthermore, the
singularly
important "19.5" number, representing the most significant portion of the
circumscribed tetrahedron, is the precise harmonic of the number 36, which
is by far one of the most harmonic numbers of all. In the triangle-shaped
"tetracys" from Pythagoras, there are 36 rows of dots starting with one dot
at the top and ending with 36 dots at the bottom. Together, this forms a
triangle, and it also represents a simple system of harmonic counting. When
we summarize all the dots in the triangle together, we come to that same
cornerstone ísolarí number, 666.
Therefore, as we look at harmonic numbers showing up in the Solar System in
Part Three, we have more reason than ever to see that they can be directly
connected with Platonic geometries. Even the speed of light itself appears
to describe a harmonic spiral that Cathie equated with 144 in his harmonic
time system based on a proportion of nine. But before we enter into our
final discussion regarding time cycles, we will finish out our look at the
history of this knowledge. By examining the trickle-down effect of Atlantean
knowledge into past and present "secret societies," we can indeed trace how
it was that literally all of the knowledge that we have been discussing was
carefully preserved.
We will explore how it was that ancient peoples chased after these Grid
energies one line at a time, through the amazing study of "ley lines" and
how they emerge all over the planet. We will also explore an amazing twist
to the story, by showing how a present-day secret society still exists which
has never lost this knowledge. This secret society was responsible for the
formation of the United States Government, and lent its hand quite directly
in the building of the United Nations Meditation Room.
We will show the
amazing quality of this room, and suggest that it is indeed a hyperdimensional "machine," built on the premises of this carefully guarded
secret knowledge that is gradually becoming available to the public.
Back to Contents
|

 Childressí article starts out by describing the most crowd-pleasing feature
in the Oregon Vortex / House of Mystery. A 100-year old shack was built over
the vortex, and within this shack, a broom is "standing rigidly straight in
the middle of the room, untouched by anyone or anything, as if it were a
spear stuck in the middle of the floor." The record time for the broom to
remain standing, according to those who run the
Childressí article starts out by describing the most crowd-pleasing feature
in the Oregon Vortex / House of Mystery. A 100-year old shack was built over
the vortex, and within this shack, a broom is "standing rigidly straight in
the middle of the room, untouched by anyone or anything, as if it were a
spear stuck in the middle of the floor." The record time for the broom to
remain standing, according to those who run the

 The one point that we need to mention here is that
Tenenís work also shows
us a very interesting principle at work in the formation the Hebrew
alphabet. Tenen explains that the Hebrew alphabetical characters represent
different shadows of a single geometric figure. That single geometric figure
is, believe it or not, a spiral shape contained within a tetrahedron! As
amazing as it must seem, all we have to do is rotate the tetrahedron into
different angular positions and then draw the shadows that result. All of
the Hebrew letters will show up in a quite natural progression as a result
of doing this.
The one point that we need to mention here is that
Tenenís work also shows
us a very interesting principle at work in the formation the Hebrew
alphabet. Tenen explains that the Hebrew alphabetical characters represent
different shadows of a single geometric figure. That single geometric figure
is, believe it or not, a spiral shape contained within a tetrahedron! As
amazing as it must seem, all we have to do is rotate the tetrahedron into
different angular positions and then draw the shadows that result. All of
the Hebrew letters will show up in a quite natural progression as a result
of doing this.