by David Wilcock

from Ascension2000 Website

recovered through WayBackMachine Website

We have indeed seen the evidence to suggest that the atom is an aether-vortex with spherical symmetry and a central axis, thus forming a spherical torus.

The Biefield-Brown effect proves that the grand solution to the mystery of “charge polarity” is that aetheric energy is flowing through the electron clouds into the nucleus. Dr. Ginzburg made a few simple and acceptable adjustments to relativity equations and produced a model that perfectly explains the behaviors of matter observed by Kozyrev in the laboratory, wherein it sheds energy and mass as it is accelerated towards the speed of light.

Through the conventional crystal molecule formations of the tetrahedron, cube and octahedron, and especially with the introduction of microclusters, icosahedral and dodecahedral quasi-crystals and the phenomenon of Bose-Einstein condensates, we now see the importance of Platonic Solids in the quantum realm.

We can no longer deny that these forces exist, as we now have irrefutable physical evidence. These new findings also reveal that we no longer need to think of atoms as individual units, but rather as harmonic aether vortexes that can merge together into greater levels of unity and coherence, such as in quasi-crystals.

And with this data in place, we now have a valid solution for all the “loose ends” of the puzzle by introducing the work of Rod Johnson.
 

BASICS OF JOHNSON’S “SEQUENTIAL PHYSICS”

What we ultimately see in Johnson’s model is the following:

• There are no “hard” particles, only groupings of energy.

• Every quantum measurement can be explained geometrically, as a form of structured, intersecting energy fields.

• Atoms are actually counter-rotating energy forms in the shape of the Platonic Solids, specifically rooted in the counter-rotation of the octahedron and tetrahedron, each vibrational/pulsational shape corresponding to a different major density of aether.

• All levels of density or dimensions in the entire Universe are structured from these two primary levels of aether, which are continually interacting with each other.

Significantly, an increasing number of advanced theorists have already been striving towards a “particle mesh” model of physics, based on the Superstring theory, where all matter in the Universe is somehow an element of an interconnected geometric matrix. However, since conventional scientists have not yet visualized Platonic Solids that are nested within each other, sharing a common axis and capable of counter-rotating, they have missed the picture for the quantum realm.

Again, in this chapter we will try to keep things simple by presenting an overview of Johnson’s model for “what’s going on” in the quantum level first, and then discuss the scientific evidence to prove it afterwards.

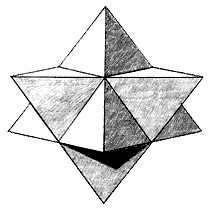
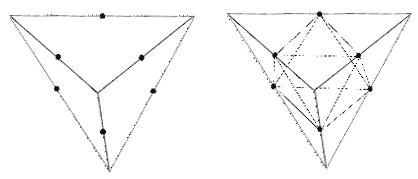
We begin our outline of the core principles of the model with a pencil-shaded illustration of the interlaced tetrahedron, which we created to show very clearly what it looks like as a three-dimensional sculpture. It is important that we have a good visual image of this structure before we try to imagine an octahedron that fits inside of it. We can clearly see that there are two tetrahedrons in the image, one with the tip pointing upwards and another with the tip pointing downwards.

Also remember that it fits perfectly inside a sphere:

Figure 4.1 – The interlaced tetrahedron.

"click" image for animation

With this structure in mind, consider the following points of the model:

• The tetrahedron and octahedron are counter-rotating within each other at the quantum level.

• Both have spherical symmetry around a shared center.

• The tetrahedron and octahedron represent two primary levels of aether density that must exist in the Universe, which we shall refer to as A1 and A2.

• The octahedral field fits perfectly in the center of the tetrahedral field, and is therefore smaller in diameter, as we can see in the next diagram:

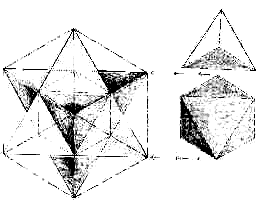
Figure 4.2 – The octahedron (R) and its fit inside the interlaced tetrahedron (L). [Lawlor, 1982]
 

Figure 4.2 shows us the octahedron inside of the interlaced tetrahedron, which in turn is inside the cube. It is quite confusing at first to try to imagine the octahedron being a free agent that can counter-rotate inside the interlaced tetrahedron. Indeed, in this form, the two geometries are completely balanced and integrated.

However, the most important part of Johnson’s physics is to see that the octahedron is “detached,” acting separately from the tetrahedral field, by rotating in the opposite direction. There are only eight possible “phase” positions that the two geometries can fit into before they again reach the harmony that we see above. In order to have a phase position, the two geometries must have some degree of direct contact with each other, such as line to line or point to point.

This is graphically illustrated in the next “phase” diagram:

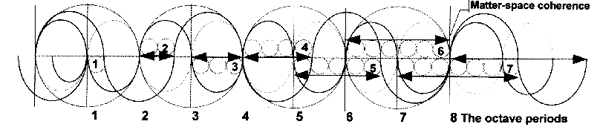
Figure 4.3 – The eight “phase positions” created by the counter-rotating octahedron and tetrahedron.
 

What we see in this diagram are two basic waves: the smaller wave that fits in each of the four main circles, representing the rotation of the octahedron, and the larger wave outside the main circle boundaries as the counter-rotation of the tetrahedron.

This diagram is by far the easiest way to show how and where the tetrahedron and octahedron will connect, and it is based on the science of “phase physics,” which was first pioneered by Kenneth Geddes Wilson as a means of mapping out large-scale geometric relationships as wave motions.

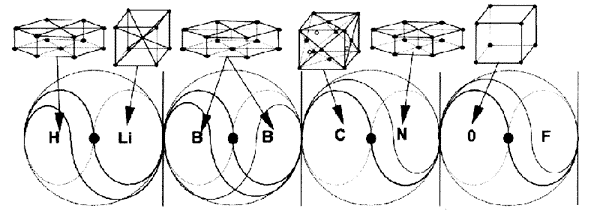
Each of the eight “phase positions” represents a different element, and this is shown in the next figure:

Figure 4.4 – The eight “phase positions” as they relate to basic crystal structures formed by the elements.
 

So, to continue:

- The tetrahedron and octahedron are both under high pressure – the tetrahedron is pushing in towards the octahedron, much as the negative electron clouds press in towards the nucleus.

- This pressure can only be released when either a node or line on one of the solids crosses a node or line on the other solid, opening up a gateway for the energy to flow.

The easiest way to visualize such a “gateway” opening would be if you cut out a hole in a piece of cardboard, and then turned on a hair dryer and held the nozzle flat against the cardboard, then sliding it towards the hole.

Until the nozzle actually reached the hole, the air has nowhere to go, and the engine will quickly run hard and overheat; but once the nozzle reaches the hole, the air has somewhere to go and the pressure is released, with the engine then relaxing. Inside the atom, via the Biefield-Brown effect, the pressure in the electron clouds is always trying to rush towards the nucleus, and unless the counter-rotating geometries connect, that pressure is blocked.

In this sense, the lines and nodes in the geometric forms could be seen as the “holes” that are “popped” in the nested spherical fields, which will allow the in-streaming pressure to flow through.

This solves one “pressure” problem, but we must also remember the pressure that is created by the counter-rotating forces of the tetrahedron and octahedron. (These are the geometries that form in the “field bubbles” of what we shall now call aether 1 (A1) and aether 2 (A2) respectively. Ancient traditions often referred to A1 and A2 as “positive and negative force.”)

Until the greatest number of “holes” have lined up between both geometries at the octave point of geometric balance, the full amount of outside pressure cannot flow towards the center. So, when the two forms “lock” together in valence periods that are not at the “octave” point, the counter-rotation of A1 and A2 is not fully balanced, causing additional pressure and lack of symmetry. A1 and A2 will then remain “stuck” in that unbalanced position if they are undisturbed by outside energy.

Most of the elements on D. Mendeleyev’s Periodic Table of the Elements are “stuck” in this manner, and therefore unstable. In this case, all naturally-occurring, non-radioactive elements are organized from left to right on the table in groups of eight. They move from a position of instability and lack of symmetry on the left to a position greater crystalline symmetry and geometric balance on the right. In Johnson’s model, it is only when we move to the Octave or eighth phase position of counter-rotation that the geometries again regain their perfect balance.

This can be visualized with the idea of sitting on a narrow stool. Obviously, the most comfortable sitting position is when your body is centered in the middle. Now simply picture trying to sit on the stool with eight different positions, starting out with only a small part of one of your legs contacting the stool. Each position will be uncomfortable, and you will not be truly in balance until you are sitting completely centered on the stool.

Thus, atoms and molecules that are not in such a state of balance are considered as “unstable” and will easily bond with other unstable atoms and molecules that hold the missing energy, in order to create equilibrium.
 

‘COVALENT’ BONDING

The first form of bonding that can occur is known as covalent bonding. This name is used since the “valence bonds” of electron clouds are believed to be “shared” between the atoms in question. As we said, there are no true “electrons,” and it is the completion of geometric symmetry between A1 and A2, the nested tetrahedron and octahedron, that forms this bond.

All elements are simply different proportional mixtures of A1 and A2, the nested tetrahedron and octahedron locked in different positions relative to each other, in Johnson’s model. The simplest example of this is that a single oxygen atom will naturally be attracted to two single hydrogen atoms to mutually blend into a water molecule, or H²O. Not surprisingly, the water molecule is shaped in the form of a tetrahedron.

In later chapters on biology we will see the interesting possibilities that arise as a result of this unique structure.
 

‘IONIC’ BONDING

The other option for basic bonding in chemistry is known as “ionic bonding.” In this case, the bonding is created by a difference in charge polarity, where a negative attracts a positive. When an element has an unbalanced charge, it is known as an ion, hence the term ionic bonding.

The simplest example would be with sodium chloride or salt, which can be written as Na+Cl-, and forms either a cube or octahedron. The pressure difference between the positive and negative ions is what attracts them together in this case. The chlorine atoms are 1.81 angstroms wide in the salt molecule, almost twice as large as the sodium atoms at 0.97 angstroms.

Ionic bonding can also occur when individual atoms of a particular element are attracted to each other and bond together two-by-two, thus creating symmetry.

The most basic example of this is a molecule of oxygen gas, written as O².

The only way that early (al)chemists were able to find these core elements such as the single oxygen atom were by disrupting basic chemical compounds through processes such as burning, freezing, mixing with acids and bases, et cetera.
 

FREQUENCY EXPANSIONS AND CONTRACTIONS

So, returning to the main point, we have eight basic positions or phases in which the tetrahedron and octahedron can be located.

However, any astute reader will have already seen that eight basic geometric positions are clearly not enough to form the entire Periodic Table; there must be some additional properties at work in order to produce the complete set of natural elements.

Figure 4.5 – Frequency contraction of tetrahedron (L) into octahedron (R).
 

Here is the key:

• Both geometric forms are also capable of expanding and contracting from their centers

• This is referred to as a change in their frequency

• When they change frequency, they form different types of geometric solids

• These solids are not just Platonics, but can be other forms as well, such as the Archimedean solids – and they are all interrelated by the “parent” tetrahedron and octahedron formations

As seen in Figure 4.5, contracting a geometric shape is as simple as bisecting each of its lines into two or more equal-sized lengths and then connecting the dots together. When we divide each line into two pieces, this is called a “second-frequency” division, whereas dividing each line into three pieces would be called a “third-frequency” division.

Starting with the tetrahedron, Buckminster Fuller demonstrated that a total of ten different frequencies (geometric shapes) could be created by this process of frequency expansion or contraction – and this is a central aspect of Johnson’s findings.

For example, the “strong” force in the atomic nucleus is known to be exactly ten times more powerful than the “weak” force in the electron clouds! (This is usually written as the square root of 100, which is 10.) No other plausible explanation for this anomaly has ever been advanced. Here, the nucleus represents the point of the greatest “infolded” geometry at the highest frequency level of contraction.

So, what we need to do is to combine the eight basic phases of counter-rotating geometry with the various frequencies of geometry that can emerge from expansion and contraction. With this in mind, the entire Periodic Table can be rendered – and ultimately you can predict whether the element will be a solid, liquid or gas, and what its freezing, melting and vaporization points will be. Johnson directs interested thinkers to the work of James Carter, who was able to render the entire Periodic Table through diagrams of spiraling motion that he called “circlons.”

Most interestingly, Carter’s “circlons” are spherical torus formations!

Carter didn’t appear to know what the spiraling, curly, cyclical “rotations within rotations” were that he was diagramming between the circlons to show the various elements, simply that they had to exist by “absolute motion.” For a more complete description we invite the reader to peruse our detailed interview article and / or his website.

In order to keep our thoughts simple for the purpose of this book, we will now simply point out some of the most obvious signs from quantum physics that Platonic geometries are indeed at work.
 

PLANCK’S CONSTANT AND THE ‘QUANTIZED’ NATURE OF LIGHT

Most of us already know that heat radiation and light are considered to be caused by the same thing – the passage of bursts of electromagnetic energy known as “photons.”

However, before the year 1900, light and heat were not thought to move in discrete “photon” units, but rather in a smooth, flowing, unbroken fashion. Physicist Max Planck was the first to discover that light and heat would move in “pulses” or “packets” of energy at the tiniest level, calculated to be about 10^-32 centimeters. (An atomic nucleus is actually the size of a planet in comparison!)

Interestingly, if you have a faster oscillation, you get bigger packets, and if you have a smaller oscillation you get smaller packets. Planck discovered that this relationship between the speed of oscillation and the size of the packet will always remain constant, regardless of how you measure it. This constant relationship between oscillation speed and packet size is known as Wein’s Displacement Law. Rigorously, Planck discovered a single number that expressed this relationship, which is now known as “Planck’s Constant.”

A recent article by Caroline Hartmann in the December 2001 issue of 21st Century Science and Technology deals specifically with Max Planck’s findings, and reveals that the puzzle created by his discoveries remains unsolved:

Today we are indebted to the continuing research of scientists like the Curies, Lise Meitner and Otto Hahn for a deeper insight into atomic structure. But the fundamental questions: what causes the motion of the electrons, is that motion constrained by certain geometrical laws, and why certain elements are more stable than others, are still not clear, and await new pioneering hypotheses and ideas. [emphasis added]

We can already see the answer to Hartmann’s question emerging in this book. As we had said, Planck’s discoveries came about through the study of heat radiation.

The introductory paragraph to Caroline Hartmann’s article is a perfect description of what he accomplished:

One hundred years ago, on December 14, 1900, the physicist Max Planck (1858-1947) announced (in a speech before the Kaiser Wilhelm Society of Berlin) his discovery of a new formula for radiation, which could describe all the regularities observed when matter was heated and began to radiate heat of various colors.

 

His new formula, however, rested on an important assumption: that the energy of this radiation is not continuous, but occurs only in packets of a certain size. The difficulty was in how to make the assumption behind this formula physically intelligible. For, what is meant by “energy packets,” which are not even constant, but vary proportionally with the frequency of oscillation (Wein’s Displacement Law)?

Hartmann continues a bit later on:

[Planck] knew that whenever you come upon an apparently insoluble problem in Nature, a higher, more complex lawfulness must lie behind it; or, in other words, there must be a different “geometry of the universe” than one had assumed before. Planck always insisted, for example, that the validity of Maxwell’s equations had to be re-established, because physics had reached a point where the so-called “physical” laws were not universally valid.

The core of Planck’s work can be stated in a simple equation, which describes how radiating matter releases energy in “packets” or bursts.

The equation is E=hv, where E equals the energy that you end up measuring, v is the vibrating frequency of the radiation that releases the energy, and h is what is known as “Planck’s Constant,” which regulates the “flow” between v and E.

Planck’s constant is listed as a value of 6.626. It is a dimensionless constant, meaning that it simply expresses a pure ratio between two values, and does not need to be assigned any specific measurement category other than that. Planck did not magically discover this constant, but rather painstakingly derived it by studying heat radiation of many different sorts.

This is the first major mystery that Johnson clears up with his research. He reminds us that in order to measure Planck’s constant, the Cartesian system of coordinates is used.

This system is named after its founder, Rene Descartes, and all it means is that cubes are used to measure three-dimensional space. This is so commonly done that most scientists don’t even consider it as anything unusual – just length, width and height in action. In experiments such as Planck’s, a small cube was used to measure the energy that moved through that area of space. This cube was naturally assigned a volume of “one” (1) in Planck’s measuring system, for the sake of simplicity.

However, when Planck wrote his constant he didn’t want it to be a decimal number, so he shifted the volume of the cube to 10. This made the constant 6.626 instead of 0.6626. What was truly important was the relationship between whatever was inside of the cube (6.626) and the cube itself (10.) Ultimately it did not matter whether you assigned the cube a value of one, ten or any other number, as the ratio would stay the same. Planck only discerned the constant nature of this ratio through rigorous experimentation over many years of time, as we said.

Now remember that depending on the size of the packet that is released, you will need to measure it with a different-sized cube. Yet, whatever is inside that cube will always have a ratio of 6.626 units to the cube’s own volume of 10 units, regardless of the sizes involved. Right away we should notice something; the value of 6.626 is very close to 6.666, which is exactly 2/3rds of 10.

So then we must ask, “What is so important about 2/3rds?”

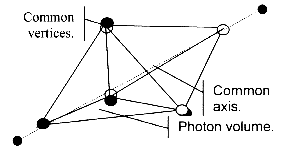
Figure 4.6 – Two tetrahedrons joined at a common face to form the “photon” measured by Planck’s constant.
 

Based on simple, measurable geometric principles explained by Fuller and others, we know that when we fit a tetrahedron perfectly inside of a sphere, it will fill exactly one-third of its total volume.

The photon is actually composed of two tetrahedrons that are joined together, as we see in figure 4.6, and they then pass together through a cube that is only big enough to measure one of them at a time. The total amount of volume (energy) that moved through the cube will be two thirds (6.666) of the cube’s total volume, to which Planck had assigned the number 10. Buckminster Fuller was the first to discover that the photon was indeed composed of two tetrahedrons joined in this way, and he announced it to the world at his Planet Planning address in 1969, after which time it was obviously forgotten.

The slight 0.040 difference between the “pure” 6.666 or 2/3rds ratio and Planck’s constant of 6.626 is caused by the permittivity of vacuum space, which absorbs some of the energy involved. This “permittivity of the vacuum” can be precisely calculated by what is known as Coulomb’s equation.

To put it in simpler terms, the aetheric energy of the “physical vacuum” will absorb a small amount of whatever energy passes through it.

This means that it will “permit” slightly less energy to pass through it than what was originally released. So, once we factor in Coulomb’s equation, the numbers work perfectly. Furthermore, if we measure space using tetrahedral coordinates instead of cubical coordinates, then the need for Planck’s equation E=hv is removed, because the energy will now be measured to be the same on both sides of the equation – thus E (energy) will equal v (frequency) with no need for a “constant” between them.

The “pulses” of energy that were demonstrated by Planck’s constant are known to quantum physicists as “photons.”

We normally think of “photons” as carriers of light, but that is only one of their functions. More importantly, when atoms absorb or release energy, the energy is transmitted in the form of “photons.” Researchers such as Dr. Milo Wolff remind us that the only thing we know for certain about the term “photon” is that it is an impulse that travels through the aether/zero-point energy field.

Now, we can see that this information has a geometric component, which suggests that the atoms must have such geometry as well.
 

BELL’S THEOREM

Another recently discovered anomaly that shows us that there is geometry at the quantum level is Bell’s Inequality Theorem.

In this case, two photons are released in opposite directions. Each photon is emitted from a separate atomic state that has been excited. Both atomic states are composed of identical atoms, and both are also decaying at the same rate. This allows two “paired” photons with the same energy qualities to be released in opposite directions at the exact same time.

Both photons are then passed through polarization filters such as mirrors, which should theoretically change their direction of travel. If you have one mirror at a 45-degree angle, then you would naturally expect the photon to make a different angular turn than another photon would make if it was reflected off of a mirror at a 30-degree angle.

However, when this experiment is actually carried out, the photons will make the exact same angular turns at the same time, regardless of the differences in the angle of the mirrors!

The degree of precision that has been brought to this experiment is staggering, as the next quote from pages 142 and 143 of Dr. Milo Wolff’s book illustrates:

The most recent experiment by Aspect, Dalibard and Roger used acousto-optical switches at a frequency of 50 MHz which shifted the settings of the polarizers during the flight of the photons, to completely eliminate any possibility of local effects of one detector on the other…

Bell’s Theorem and the experimental results imply that parts of the universe are connected in an intimate way (i.e. not obvious to us) and these connections are fundamental (quantum theory is fundamental.) How can we understand them? The problem has been analyzed in depth (Wheeler & Zurek 1983, d’Espagnat 1983, Herbert 1985, Stapp 1982, Bohm & Hiley 1984, Pagels 1982, and others) without resolution.

 

Those authors tend to agree on the following description of the non-local connections:

1. They link events at separate locations without known fields or matter
2. They do not diminish with distance; a million miles is the same as an inch
3. They appear to act with speed greater than light

Clearly, within the framework of science, this is a perplexing phenomenon.

What Bell’s Theorem is showing us is that the energetically-paired “photons” are actually joined together by a single geometric force, such as the tetrahedron, which continues expanding into a larger size as the photons move apart.

The photons will continue to maintain the same angular phase position relative to each other as the geometry that is between them expands.
 

THE ELECTROMAGNETIC WAVE

Our next point of investigation is the electromagnetic wave itself, since Einstein determined that matter is made from electromagnetic energy. As most of us are aware, the electromagnetic wave has two components – the electrostatic wave and the magnetic wave, which move together. Interestingly, the two waves are always perpendicular to each other.

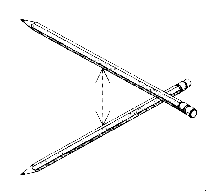
To visualize what is going on here, Johnson asks us to take two pencils of equal length and hold them perpendicularly to each other, also using the basic length of the pencil for the distance that separates them:

Figure 4.7 – Two pencils at 90-degree angles from each other, held equidistantly apart.
 

Now we can connect each tip of the top pencil to each tip on the bottom pencil.

When we do this, we will form a four-sided object made of equilateral triangles between the two pencils – we will have a tetrahedron. We can work the same process with the electromagnetic wave, by having the total height of the electrostatic or magnetic wave (which both have the same height or amplitude) as our basic length, which was shown in figure 4.7 as pencils.

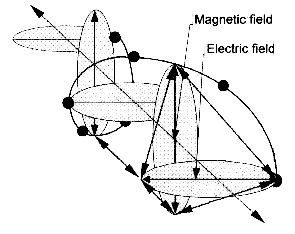
Here in figure 4.8, we can see how the electromagnetic wave is actually tracing itself over a “hidden” (potential) tetrahedron when we connect the lines together using this same process:

Figure 4.8 – The hidden tetrahedral relationship in the electromagnetic wave.
 

It is important to mention here that this mystery has been continually discovered by various thinkers, only to be forgotten to science once more.

The work of Lt. Col. Tom Bearden has rigorously shown that James Clerk Maxwell knew it was there when he wrote his complex “quaternion” equations, but Oliver Heaviside later distorted the model down to four simple quaternions and ruined the hidden tetrahedral “potential” inside. This hidden tetrahedron was also seen by Walter Russell, and later by Buckminster Fuller.

Johnson was not aware of any of these previous breakthroughs when he first discovered it himself.
 

GELL-MANN’S “EIGHTFOLD WAY”

The next enigma comes to us when we study the subatomic “particles” known as quarks.

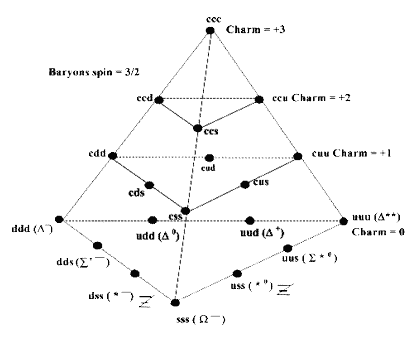
When an atomic structure was suddenly shattered, brief tracks would emerge that would fly away from the normal spiraling “particle” path in a bubble chamber, and they were named “quarks.” These “quarks” would disappear very quickly after they were first released.

The geometry of their movements was carefully analyzed, since the only thing you can truly detect in a vapor-trail analysis is different geometric forms of movement. Many different forms of “quarks” were discovered, each with different geometric properties, misleadingly called such things as “color,” “charm” and “strangeness.” Murray Gell-Mann was the first to discover a unified model that showed how all these different geometric properties were interrelated, and he called it the “Eightfold Way.”

Remarkably, the unified geometric structure that we see is a tetrahedron:

Figure 4.9 – The tetrahedron as seen in Gell-Mann’s “Eightfold Way” organization of “quarks.”
 

So what exactly are we seeing here?

Each dot is obviously a different “quark.” Johnson tells us that “quarks” are released when the aetheric energy flow of the tetrahedron inside the atom is suddenly shattered. For a brief moment of time, the shattered energy fragments that are released will continue to flow with the same rotational / geometric properties as they had when they were bound in the atom, but they will very quickly dissolve back into the aether afterwards.

One wouldn’t necessarily see all of the different “quarks” just by shattering one atom, since the angle at which the atom is shattered determines what part of its inner geometric Unity will be released. This is why the quarks had to be painstakingly studied separately. Even more interestingly, other “infolded” geometric frequencies such as the cuboctahedron are in Gell-Mann’s model as well; this tetrahedron is just one of three different hierarchies that he discovered.

Again, the mainstream scientific world sees Gell-Mann’s Eightfold Way as nothing more than a convenient geometric organization, but with no further meaning than that.

In this next excerpt, Dr. Milo Wolff alludes to the fact that the geometry might be the solution to understanding the structure of the “nuclear space resonances” in the quantum realm, from page 198 of his book:

Another interesting problem with a valuable result is to see if a way can be found to match up nuclear space resonances with the group-theory explanation of the nuclear particle zoo. One of the names of that theory is the Eight-fold way discovered by Gell-mann and Ne’eman in 1960. It cleverly uses geometric groupings of the various particles to determine their parameters: spin, parity, isotope number and strangeness number.

 

The group theory has not yet revealed a physical structure such as space resonances. If there is a relation it is logical to expect that the solutions of the SR wave equation would have orthogonal properties that match the Eight-fold way. It is an exciting prospect to attempt.

Interestingly, just as we were finishing this portion of the book, we were contacted by Dr. R.B. Duncan, who has a quite detailed and meticulous work published online that explains the structure of the atom based on the geometry of group theory that Wolff was mentioning above.

Duncan had worked on this problem for thirty years of his life before publishing a solution!
 

THE ENIGMAS OF “SPIN” AND TORSION EXPLAINED

Figure 4.10 – 180-degree spin angles of “electrons” caused by impulses moving over octahedral energy forms.
 

The next piece of evidence that we need to consider is spin.

Physicists have known for many years now that energy particles “spin” as they travel. For example, “electrons” appear to be continually making sharp 180-degree turns or “half spins” as they move through the atom. “Quarks” are often seen to make “one thirds” and “two thirds” spins when they travel, which allowed Gell-Mann to organize their movements into the tetrahedron and other geometries. No one in the mainstream has provided a truly adequate explanation for why this is happening.

Johnson’s model shows that the 180-degree “spin” of the electron clouds is being caused by the movement of the octahedron, as seen above in Figure 4.10. It is important that we realize that the 180 degree movement actually comes from two 90-degree turns for each octahedron. The octahedron must “flip over backwards,” i.e. 180 degrees, to remain in the same position in the matrix of geometry that surrounds it.

The tetrahedron must make either 120-degree (1/3 spin) or 240-degree (2/3 spin) rotations in order to have the same position. This will be explained more simply in section 4.9 just below here. (Other aether theorists such as Wolff, Crane, Ginzburg and Krasnoholovets have their own fluid-flow-based explanations for the phenomenon of half-spin.)

The enigma of the spiraling movement of torsion waves is also explained by this same process. No matter where you are in the Universe, even in “vacuum space,” the aether will always be pulsating in these geometric forms, forming a matrix. Therefore, any impulse of momentum that travels through that aether will have to trace a path across the faces of these geometric “fluid crystals” in the aether.

Thus, the spiraling movement of the torsion wave is caused by the simple geometry that it must pass through as it travels.
 

THE FINE-STRUCTURE CONSTANT

We have included this section for those who wish to see just how far the “matrix” model goes.

The fine structure constant is another aspect of quantum physics that few mainstream people have ever even heard of, probably since it is a totally unexplained embarrassment to the scientific mainstream that clings to particle-based models.

Picture now that an electron cloud is like a flexible rubber ball, and each time a “photon” of energy is absorbed or released, (known as coupling,) the cloud stretches and flexes as if it had bounced.

The electron cloud will always be “bumped” in a fixed, exact proportional relationship to the size of the photon. This means that if you have larger photons you will get larger “bumps” on the electron cloud, and smaller photons create smaller “bumps” on the electron cloud. This relationship remains constant, regardless of size. The fine-structure constant is another “dimensionless” number like Planck’s constant, meaning that we will get the same proportion regardless of how we measure it.

This constant has been continuously studied by spectroscope analysis, and the highly revered physicist Richard P. Feynman explained the mystery in his book The Strange Theory of Light and Matter.

(We should again remember here that the word “coupling” simply means the joining together or separation of a photon and an electron:)

There is a most profound and beautiful question associated with the observed coupling constant e – the amplitude for a real electron to emit or absorb a real photon. It is a simple number that has been experimentally determined to be close to 0.08542455. My physicist friends won't recognize this number, because they like to remember it as the inverse of its square: about 137.03597 with an uncertainty of about two in the last decimal place. It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it.

Immediately you would like to know where this number for a coupling comes from: is it related to pi or perhaps to the base of natural logarithms? Nobody knows, it is one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say that the "hand of God" wrote that number, and "we don't know how He pushed His pencil."

 

We know what kind of a dance to do experimentally to measure this number very accurately, but we don't know what kind of a dance to do on a computer to make this number come out – without putting it in secretly. [emphasis added]

In Johnson’s model, the problem of the fine-structure constant has a very simple, academic solution.

As we said, the photon travels along as two tetrahedrons that are paired together, and the electrostatic force inside the atom is maintained by the octahedron. By simply comparing the volumes between the tetrahedron and octahedron when they collide, we get the fine structure constant.

All we do is divide the tetrahedron’s volume when it is surrounded (circumscribed) by a sphere into the octahedron’s volume when it is surrounded by a sphere, and we will get the fine-structure constant as the difference between them. In order to show how this is done, some additional explanation is required.

The phase-wave diagrams that we saw earlier in this chapter (figs. 4.3 and 4.4) showed us the angular relationships between the octahedron and tetrahedron. Since a tetrahedron is entirely triangular no matter how it is rotated, the three tips on any of its faces will divide a circle up into three equal pieces of 120 degrees each.

Therefore, you only need to rotate the tetrahedron by 120 degrees in order to bring it back into balance with the matrix of geometry that surrounds it, so that it is in the same position as it was before. This is easy to see if you visualize a car with triangular wheels, and you wanted to move it forward just enough that the wheels would look the same again. Each of the triangular wheels would have to turn 120 degrees to do this.

Now in the case of the octahedron, it must always be turned “upside down” or 180 degrees in order to regain its balance. If you want to see this with the car analogy, then the wheels would need to be in the classic “diamond” shape that you see on a deck of cards. In order to get the diamond to look exactly the same as when you started, you have to flip it upside down, by 180 degrees.

This next quote from Johnson explains the fine-structure constant based on this information:

[When you] see the static electric field as the octahedron and the dynamic magnetic field as the tetrahedron, then the geometric relationship [between them] is 180 to 120. If you see them as spheres defined by radian volumes, then simply divide them into each other and you have the fine structure constant.

A “radian volume” simply means that you calculate the volume of an object from its radius, which is half of the width of the object. (For those who wish to test the math out themselves, simply take the sine of 180 degrees and divide it by the sine of 120 degrees, then run that number through Coulomb’s equation to account for the slight loss of energy that happens when a pulsation is moving through the aether.) When this simple process of dividing the two “radian volumes” into each other is performed, the fine-structure constant will be the result.

Interestingly, while Johnson has shown that the fine-structure constant can be seen as the relationship between the octahedron and tetrahedron as energy moves from one to the other, Jerry Iuliano discovered that it can also be seen in the “leftover” energy that is produced when we collapse a sphere into a cube, or expand a cube into a sphere!

These expanding or collapsing changes between the two objects are known as “tiling,” and Iuliano’s calculations were not very difficult to perform; it was simply that no one had thought to try it before. In Iuliano’s calculations, the volume of the two objects does not change; both the cube and the sphere have a volume that he set at 8pi times pi squared. When we tile them into each other, the only difference between the cube and sphere is in the amount of surface area. The extra surface area between the two is precisely equal to the fine-structure constant.

Immediately the reader should ask,

“How can the fine structure constant be a relationship between the octahedron and tetrahedron and also be a relationship between the cube and the sphere at the same time?”

This is another aspect of the magic of “symmetry” in action, where we see that different geometric forms can have similar properties, since they all nest inside of each other with perfect harmonic relationships. Both Johnson and Iuliano’s perspectives show us that we are dealing with a geometrically structured aetheric energy at work in the atom.

It is also important to remember that what Iuliano’s finding shows us is the classic geometry of the “squared circle.”

This has long been a central element in the esoteric traditions of “sacred geometry,” as it was believed to show the balance between the physical world, represented by the square or cube, and the spiritual world, represented by the circle or sphere. Now we can see that this was yet another example of “hidden knowledge” that was encoded in a metaphor, so that eventually people in our time would regain the true understanding of the secret science behind it.

They knew that once we discovered the fine-structure constant, we probably would not understand what we had observed, so this ancient knowledge was left behind to show us the key.
 

A UNIFIED MODEL

Now, with the data that we have seen from Johnson’s physics and its realization in the science of microclusters, quasi-crystals and Bose-Einstein condensates, we do indeed have a unified quantum model.

Our presentation of Johnson’s physics has been designed to be as simplified and streamlined as possible, so anyone who would attempt to challenge the model scientifically would be required to read more about it in order to truly grasp its many nuances. Yet, for those who have an open mind, the data that we have presented here is more than enough to prove the point.

The key is that sacred geometry has always existed in the quantum realm; it just remained undiscovered amongst the various anomalies of quantum physics that had remained unexplained until this time, as the mainstream continues to be shackled to outmoded “particle” models.

In this new model, we no longer have to restrain atoms to a certain size; they are capable of expanding and maintaining the same properties. Once we fully understand what is going on in the quantum realm, we can design materials that are extremely hard and extremely light, since we are now aware of the exact geometric arrangements that will cause them to bond together most effectively.

We remember that pieces of wreckage from the Roswell Crash were said to be unbelievably lightweight, yet they were so strong that they could not be cut, burned or damaged in any way. This is the type of material that we will be able to build once we fully understand the new quantum physics.

We remember that quasi-crystals are very good at storing heat, and also that they often do not conduct electricity, even if the metals involved are normally good conductors. Similarly, microclusters do not allow magnetic fields to penetrate inside the clusters themselves. What Johnson’s physics tells us is that such a geometrically perfect structure has perfect bonding all the way through, and thus no thermal or electromagnetic energy can pass through it.

The geometry is so compact and precise inside that there is literally no “room” for a current to move through the molecules.

Now that we have a relatively complete aetheric model for quantum physics, we are ready to move forward and show how such geometric forces continue to have their influences on larger scales of size, namely in the formations known as the Global Grid.

Much of this material is a review from previous volumes, but it is nevertheless important that we cover it once more.

After we establish this crucial link between the geometry of the quantum and the geometry of the macro, effectively proving the existence and importance of these new theories, we will move on to delineate an entirely new model of the Cosmos that is based on all of the principles that we have discussed up until this point.