Electrical Circuits

It's hard to grasp the idea that electric circuits can resonate because we can't see it happening. Still, it's one of the most useful and common forms of resonance.

Resonance can occur in something called an RLC circuit. The letters stand for the different parts of the circuit. R is for resistor. These are devices which convert electrical energy into thermal energy. In other words, they remove energy from the circuit and convert it to heat. L stands for inductor. (How they came up with L for inductor is hard to understand.) Inductance in electric circuits is like mass or inertia in mechanical systems.

It doesn't do much until you try to make a change. In mechanics the change is a change in velocity. In an electric circuit it is a change in current. When this happens inductance resists the change. C is for capacitors which are devices that store electrical energy in much the same way that springs store mechanical energy. An inductor concentrates and stores magnetic energy, while a capacitor concentrates charge and thereby stores electric energy.

Of course, the first step in understanding resonance in any system is to find the system's natural frequency. Here the inductor (L) and the capacitor (C) are the key components. The resistor tends to damp oscillations because it removes energy from the circuit.

For convenience, we'll temporarily ignore it, but remember, like friction in mechanical systems, resistance in circuits is impossible to eliminate.

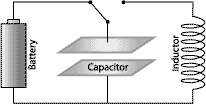
Figure 1: Switch position for charging the capacitor


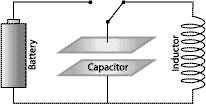
Figure 2: Switch position for making the circuit oscillate
 

We can make a circuit oscillate at its natural frequency by first storing electrical energy or, in other words, charging its capacitor as shown in Figure 1. When this is accomplished the switch is thrown to the position shown in Figure 2.

At time = 0 all of the electrical energy is stored in the capacitor and the current is zero (see Figure 3). Notice that the top plate of the capacitor is charged positively and the bottom negatively. We can't see the electrons' oscillation in the circuit but we can measure it using an ammeter and plot the current versus time to picture what the oscillation is like.

Note that T on our graph is the time it takes to complete one oscillation.

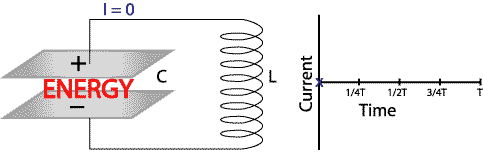
Figure 3: Beginning of oscillation
 

Current flows in a clockwise direction (see Figure 4). The energy flows from the capacitor into the inductor. At first it may seem strange that the inductor contains energy but this is similar to the kinetic energy contained in a moving mass.

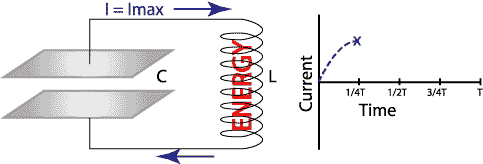
Figure 4: time = 1/4T
 

Eventually the energy flows back into the capacitor, but note, the polarity of the capacitor is now reversed. In other words, the bottom plate now has the positive charge and the top plate the negative charge (see Figure 5).

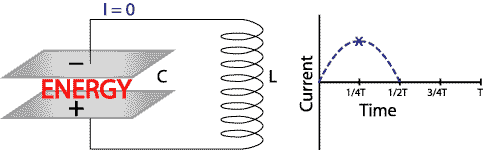
Figure 5: time = 1/2T
 

The current now reverses itself and the energy flows out of the capacitor back into the inductor (see Figure 6). Finally the energy fully returns to its starting point ready to begin the cycle all over again as shown in Figure 3.

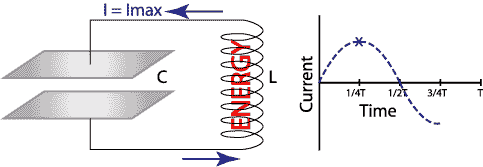
Figure 6: time = 3/4T
 

The frequency of the oscillation can be approximated as follows:

f = 1 / 2π (LC)^0.5


Where: f = frequency
           L = Inductance
           C = Capacitance

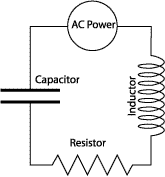
Figure 7: Resonating circuit

In real-world LC circuits there's always some resistance which causes the amplitude of the current to grow smaller with each cycle. After a few cycles the current diminishes to zero. This is called a "damped sinusoidal" waveform. How fast the current damps to zero depends on the resistance in the circuit. However, the resistance does not alter the frequency of the sinusoidal wave. If the resistance is high enough, the current will not oscillate at all.

Obviously, where there's a natural frequency there's a way to excite a resonance. We do this by hooking an alternating current (AC) power supply up to the circuit as shown in Figure 7. The term alternating means that the output of the power supply oscillates at a particular frequency. If the frequency of the AC power supply and the circuit it's connected to are the same, then resonance occurs. In this case we measure the amplitude or size of the oscillation by measuring current.

Note in figure 7 that we have put a resistor back in the circuit. If there is no resistor in the circuit the current's amplitude will increase until the circuit burns up. Increasing resistance tends to decrease the maximum size of the current's amplitude but it does not change the resonant frequency.

As a rule of thumb, a circuit will not oscillate unless the resistance (R) is low enough to meet the following condition:

R = 2 (L/C)^0.5

Resonance in circuits might be just a curiosity except for its usefulness in transmitting and receiving wireless communications including radio, television, and cell phones. Transmitters used for sending signals are typically circuits designed to resonate at a specific frequency called the carrier frequency. The transmitter is then connected to an antenna which radiates electromagnetic waves at the carrier frequency.

An antenna on the other end receives the signal and feeds it to yet another circuit also designed to resonate at the carrier frequency. Obviously, the antenna receives many signals at various frequencies not to mention background noise. The resonating circuit essentially selects the correct frequency from among all the unwanted ones.

With an amplitude modulated (AM) radio the amplitude of the carrier frequency is modified so that it contains the sounds picked up by a microphone. This is the simplest form of radio transmission but is very susceptible to noise and interference.

Frequency modulated or FM radio solves many of the problems of AM radio but at the price of higher complexity in the system. In an FM system sounds are electronically transformed into small changes in the carrier frequency. The piece of equipment which performs the transformation is called a modulator and is used with the transmitter.

In addition, a demodulator has to be added to the receiver to convert the signal back into a form which can be played on a speaker.



References

Physics for Scientists and Engineers 4th Edition Volume 2, Raymond A. Serway, Saunders College Publishing, p.949
 

Acknowledgements

• This project was supported by a National Science Foundation Research Experience for Teachers grant as part of Clemson University's Summer Undergraduate Research Experience in Wireless Communications.

For more information about wireless communication and the electromagnetic spectrum visit The Hidden World of the Electromagnetic Spectrum.

Back to Contents