August 2006

from Antikythera-Mechanism Website

The Antikythera Mechanism is a unique Greek geared device, constructed around the end of the 2^nd Century BC.

From previous work^{1,2,3,4,5,6,7,8,9} it is known that it calculated and displayed celestial information, particularly cycles such as the phases of the moon and a luni-solar calendar. Calendars were important to ancient societies10 for timing agricultural activity and fixing religious festivals. Eclipses and planetary motions were often interpreted as omens, while the calm regularity of the astronomical cycles must have been philosophically attractive in an uncertain and violent world.

Named after its place of discovery in 1901 in a Roman shipwreck, the Mechanism is technically more complex than any known device for at least a millennium afterwards. Its specific functions have remained controversial^11,12,13,14 because its gears and the inscriptions upon its faces are only fragmentary. Here we report surface imaging and high-resolution X-ray tomography of the surviving fragments, enabling us to reconstruct the gear function and double the number of deciphered inscriptions.

The Mechanism predicted lunar and solar eclipses based on Babylonian arithmetic-progression cycles. The inscriptions support suggestions of mechanical display of planetary positions^9,14,16, now lost. In the second century BC, Hipparchos developed a theory to explain the irregularities of the Moon's motion across the sky caused by its elliptic orbit.

We find a mechanical realization of this theory in the gearing of the Mechanism, revealing an unexpected degree of technical sophistication for the period.

Figure 1:

The surviving fragments of the Antikythera Mechanism. The 82 fragments that survive in the National Archaeological Museum in Athens are shown to scale. A key and dimensions are provided in Supplementary Notes 1 (Fragments).

 

The major fragments A, B, C, D are across the top, starting at top left, with E, F, G immediately below them. 27 hand-cut bronze gears are in fragment A and one gear in each of fragments B, C and D. Segments of display scales are in fragments B, C, E and F. A schematic reconstruction is given in Figure 2.

It is not certain that every one of the remaining fragments (numbered 175) belong to the Mechanism. The distinctive fragment A, which contains most of the gears, is approximately 180 x 150 mm in size.

 

We have used three principal techniques to investigate the structure and inscriptions of the Antikythera Mechanism.

1. 3-dimensional Xray microfocus computed tomography17 (CT), developed by XTek Systems Ltd. The use of CT has been crucial in making the text legible just beneath the current surfaces.

2. Digital optical imaging to reveal faint surface detail using Polynomial Texture Mapping (PTM)18,19 , developed by Hewlett-Packard Inc.

3. Digitized high quality conventional film photography.
    

The bronze Mechanism (Figure 1 above), probably hand-driven, was originally housed in a wooden-framed case¹ of (uncertain) overall size 340 x 180 x 90 mm.

It had front and back doors, with astronomical inscriptions covering much of the exterior of the Mechanism (Figure 2 below). Our new transcriptions and translations of the Greek texts are given in Supplementary Notes 2 (Glyphs & Inscriptions).

Figure 2:

A schematic view of the Mechanism to illustrate the position of major inscriptions and dials. The Front Dial has two concentric scales. The inner scale shows the Greek Zodiac with 360 divisions.

 

There are occasional Greek letters denoting references to the Parapegma inscription, and we add three further reference letters (Z, H, Θ) to Price’s description1. The Parapegma is a star almanac showing rising and settings at dawn or evening of particular stars or constellations, which we will discuss elsewhere. Its form is consistent with a late 2nd Century BC date. The outer (originally) movable scale is a Calendar carrying the Egyptian names of the months with Greek letters.

 

The Egyptian Calendar of 365 days, with twelve 30day months and 5 extra (epagomenai) days was in standard use in Greek astronomy. The effect of the extra quarter day in a year could be corrected by turning the scale one day every four years – and a sequence of holes to take a locking pin is observed under the scale. We find that spacing of the holes is indeed what would be expected for a total of 365 days, with a possible range 363365.

 

The position of the Sun and Moon would have been indicated by pointers across the dial scales, and a device7 showing the phase of the Moon was probably carried round on the lunar pointer. It is not clear whether the Sun position pointer would have been separated from a date pointer, or whether any planetary positions might have been displayed.

 

The spiral Upper Back Dial displays the lunisolar Metonic sequence of 235 lunar months with a subsidiary dial showing the Callippic cycle, while the spiral Lower Back Dial displays the 223 lunar month Saros eclipse cycle with a subsidiary dial showing the Exeligmos cycle.
 

The detailed form of the lettering can be dated to the second half of the 2nd Century BC, implying that that the Mechanism was constructed during the period 150-100 BC, slightly earlier than previously suggested¹.

This is consistent with a date of around 80-60 BC of the wreck^1,20 from which the mechanism was recovered by some of the first underwater archaeology. We are able to complete the reconstruction1 of the Back Door inscription with text from fragment E, and characters from fragments A and F.

The Front Door is mainly from fragment G. The text is astronomical with many numbers that could be related to planetary motions. The use of “sterigmos [ΣΤΗΡΙΓΜΟΣ] – station or stationary point” means where a planet’s apparent motion changes direction and the numbers may relate to planetary cycles. The Back Door inscription mixes mechanical terms about construction (“trunnions”, “gnomon”, “perforations”) with astronomical periods.

Of the periods, 223 is the Saros eclipse cycle (see 'Box' below for brief explanation of astronomical cycles and periods).

We discover the inscription “spiral divided into 235 sections”, which is the key to understanding the function⁶ of the Upper Back Dial. The references to “golden little sphere” and “little sphere” probably refer to the front zodiac display for the Sun and Moon – including phase for the latter.

The text near the Lower Back Dial includes “Pharos” and “From South (about/around)… Spain ten”. These geographical references, together with previous readings¹ of “Towards the East”, “WestNorthWest” and “WestSouthWest” suggest an eclipse function for the dial, since solar eclipses occur only at limited often recorded ^22,23,24 geographical sites, and winds were in antiquity with eclipse observations.

Possibly this information was added to the Mechanism during use.

Turning to the dials themselves, the Front Dial displays the position of the Sun and Moon in the Zodiac, and a corresponding calendar1 of 365 days that could be adjusted for leap years. Previously¹, it was suggested that the Upper Back Dial might have five concentric rings with 47 divisions per turn, showing the 235 months of the 19year Metonic Cycle. A later proposal ⁵ augments this with the Upper Subsidiary Dial showing the 76year Callippic Cycle.

Our optical and CT imaging confirm these proposals, with 34 scale markings discovered on the Upper Back Dial. Based on a statistical analysis analogous to that described for gear tooth counts below, we confirm the 235 total divisions.

We also find from the CT that the subsidiary dial is indeed divided into quadrants^1,6, as required for a Callippic Dial.

In agreement with the Back Door inscription, we also substantiate the perceptive proposal^5,25 that the dial is in fact a spiral, made from semicircular arcs displaced to two centers on the vertical midline. In the CT of fragment B we find a new feature that explains why the dial is a spiral: a “PointerFollower” device (see Figure 3 below) traveled around the spiral groove to indicate which month (across the five turns of the scale) should be read.

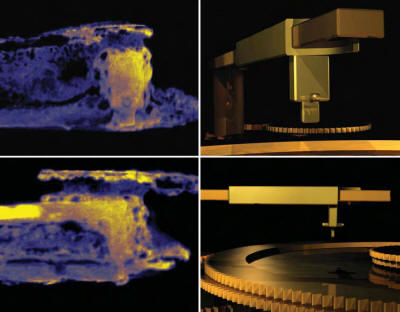
Figure 3:

The “pointer-follower” lunar month indicator of the Upper Back Dial. On the left, false-color sections through CT images, analyzed with VG-Studio Max software by Volume Graphics GmbH.

 

These show two views at right angles of the pointer-follower in the Metonic dial in fragment B. On the right, a computer reconstruction of the device from two different angles (with the Metonic scale omitted for clarity). The pin was constrained to follow the groove between the spiral scales (the scale is shown in Figure 4 below), causing the device to slide along the month pointer to indicate which ring on the spiral scale specified the month. A similar pointer-follower would have been present on the Lower Back (Saros) Dial.

 

The Metonic dial would have required resetting every 19 years, the Saros dial after 18 years. The groove-pin may have been held in place by the small pin through the front of the device, enabling its removal for resetting.

 

 

Figure 4:

Reconstruction of the Back Dials. A composite of fragments A, B, E and F. The Metonic Calendar is at top, with its subsidiary Callippic dial. The Saros eclipse cycle is below, with its subsidiary Exeligmos dial.

 

The 16 observed eclipse glyphs are shown in turquoise on the Saros dial, with 35 hypothetical glyphs in violet. The hypothetical glyphs are based on the criterion that 99% of the 121 sequences exactly matching the observed glyphs have an eclipse at the month position. Both main dials would have a “pointerfollower” (see Figure 3 above) to indicate the relevant lunar month on the spiral.

 

The monthly divisions on the Metonic Upper Back Dial are not simply scribed directly across all five turns, as might be expected for simplicity of construction. There are small misalignments, implying a systematic attempt at marking full (30day) and hollow (29day) months. The incomplete data does not allow good analysis, other than a hint of bimodality in the interval distribution.

 

If the marking out of the scale were carried out using the Mechanism’s gearing, then this would greatly predate known “dividing engines”27 by many centuries.
 

From our CT data of the 48 scale divisions observed in fragments A, E and F, we establish 223 divisions in the fourturn^5,25 spiral on the Lower Back Dial, the spiral starting at the bottom of the dial.

This is the Saros eclipse cycle, whose number is on the Back Door inscription. The 54-year Exeligmos cycle of three Saros cycles is shown on the Lower Subsidiary Dial.

Between the scale divisions of the Saros Dial we have identified 16 blocks of characters, or “glyphs” (see 'Glyphs & Inscriptions', below) at intervals of one, five and six months.

Symbols (glyphs) in the Saros spiral scale

Lunar Glyphs

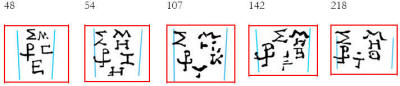
Solar Glyphs

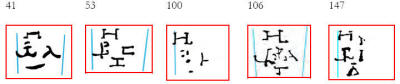
Lunar & Solar Glyphs

These are eclipse predictions and contain either Σ for a lunar eclipse (from ΣΕΛΗΝΗ, Moon) or H for a solar eclipse (from ΗΛΙΟΣ, Sun) or both.

A correlation analysis (analogous to DNA sequence matching) with historic eclipse data26 indicates that over a period of 400 – 1 BC the sequence of eclipses marked by the identified glyphs would be exactly matched by 121 possible start dates.

The matching only occurs if the lunar month starts at first crescent and confirms this choice of month start in the Mechanism.

The sequences of eclipses can then be used to predict the expected position of glyphs on the whole dial, as seen in Figure 4 far below. The dial starts and finishes with an eclipse. Although Ptolemy indicates that the Greeks recorded eclipses in the 2nd century BC, the Babylonian Saros Canon ^22,23,24 is the only known source of sufficient data to construct the dial.

The functions of the Mechanism are determined by the tooth counts of the gears. These are based mainly on the CT, using angular measurement from a nominal centre to the remains of tooth tips. In a few cases all teeth can be seen, but many gears are incomplete. Counts are established by fitting models with regularly spaced teeth and minimizing the r.m.s. deviation from the measurements—varying the centre in software (when unclear) to find the best-fit solution or solutions.

We have adopted a systematic nomenclature of lower case letters for the axis of the gear, with numbering increasing with ordering from the front of the Mechanism. Hypothetical (lost) gears are denoted by italics.

Several models have been proposed for the gear trains^1,2,4,5,6,8. We agree with the assumption of four missing gears (n1, n2, p1, p2) to drive the Metonic and Callippic Dials ⁴.

We propose a new reconstruction for the other trains, which uses all extant gears (except the lone r1 from the separate fragment D). The proposed model is shown in Figure 5 below.

We require the assumption of only one further gear (m3) whose proposed shaft is clearly broken off in the CT.

Figure 5:

New Reconstruction of the Gear Trains. A schematic sectional diagram (not to scale) of the gearing, following the style of Price¹ and Wright⁴. The viewpoint is looking down from the top right of the Mechanism, and is stretched in the direction of the main axes to show the structure.

 

Features that are outlined or labeled in red are hypothetical. Gears are lettered with their shaft, and numbered with increasing distance from the Front Dial. The two-or-three digit number on the gear is its actual or assumed tooth count (See Supplementary Notes 3 - Gears). Hypothetical gears n1, n2, p1, p2 have been proposed previously, the gear m3 on the broken-off shaft m is our addition.

 

All gears, except the lone one in fragment D, are now accounted for in the Mechanism. The function of the trains is outlined in the text. We find no evidence in the CT for an idler wheel carried on e3 and between e5 and k1 or between k2 and e6, as has been previously proposed^1,2,4. The CT shows a pin through axis e between gears e1 and e2.

 

We believe its purpose is to retain the square-bossed e1 on the shaft, but its passage right through the axis rules out previous reconstructions^1,2,4 where e1 and e2 were joined by an outer pipe rotating around the shaft e.

 

Of particular note is the dual use of the large gear, e3, at the back of the Mechanism, which has found no use in previous models. In our model, it is powered by m3 as part of a fixed-axis train that turns the Saros and Exeligmos Dials for eclipse prediction and also doubles as the “epicyclic table” for the gears k1, k2.

These are part of epicyclic gearing that calculates the theory of the irregular motion of the moon, developed by Hipparchos sometime between 146 and 128 BC²⁸—the “first anomaly”, caused by its elliptical orbit about the Earth. The period of this anomaly is the period from apogee to apogee (the anomalistic month). To realize this theory, the mean sidereal lunar motion is first calculated by gears on axes c, d and e and this is then fed into the epicyclic system.

As explained in Figure 6 below, a pin-and-slot device on the epicyclic gears k1 and k2, clearly seen in the CT, provides the variation.

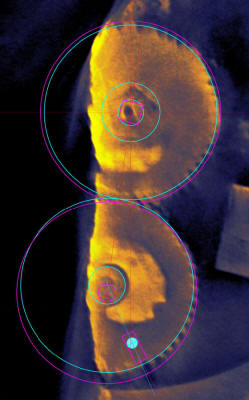
Figure 6:

The “Hipparchos” Lunar Mechanism mounted on gear e3. The figure is based on a CT slice of part of fragment A, showing (top) shaft e and (bottom) shaft k. The complete geometry cannot be seen in a single CT slice. The two gears on the e axis (e5 and e6) are coaxial, while the two k gears rotate on slightly displaced axes. k1 has a pin on its face that engages with a radial slot in k2 (and this was previously reported5).

 

In the figure the pitch circles of e5 and k1 are shown in turquoise and those of e6 and k2 in pink. The gear e5 drives k1, which drives k2 via the pin-and-slot introducing a quasi-sinusoidal variation in the motion, which is then transmitted to e6. Our estimate of the distance between the arbors on the k gears is about 1.1 mm, with a pin distance of 9.6 mm, giving an angular variation of 6.5o.

 

According to Ptolemy¹⁵, Hipparchos made two estimates for a lunar anomaly parameter, based on eclipse data, which would require angular variations of 5.9˚ or 4.5˚ here – although estimates of the anomaly from Babylonian astronomy were generally larger. The difference from our estimated value is probably not significant given the difficulty of precise measurement of the axes in the CT.

 

The harmonic variation, together with the effect of carrying the gears on e3 which rotates at the period of the Moon’s apogee around the Earth, would simulate the correct variation for the Moon’s mean (sidereal) rotation rate on the Front Dial. An (unexplained) regular pentagon is visible at the centre of gear e5.

 

It is tempting to associate the conception of the Mechanism with Hipparchos himself, but he was not the first to assume eccentric or epicyclic models.

 

This was previously identified4, but rejected as a lunar mechanism.

The remarkable purpose of mounting the pin-and-slot mechanism on the gear e3 is to change the period of variation from sidereal month (i.e. the time taken for the Moon to orbit the Earth relative to the zodiac), which would occur if k1 and k2 were on fixed axes, to anomalistic month—by carrying the gears epicyclically at a rate that is the difference between the rates of the sidereal and anomalistic months, i.e. at the rate of rotation of about 9 years of the Moon’s apogee.

Gears with 53-teeth are awkward to divide. So it may seem surprising that the gearing includes two gears with 53 teeth (f1, l2), whose effects cancel in the train leading to the Saros Dial. But the gearing has been specifically designed so that the “epicyclic table” e3 turns at the rate of rotation of the Moon’s apogee—the factor 53 being derived from the calculation of this rotation from the Metonic and Saros cycles, which are the basis for all the prime factors in the tooth counts of the gears. 

The establishment of the 53 tooth count of these gears is powerful confirmation of our proposed model of Hipparchos’ lunar theory. The output of this complex system is carried from e6 back through e3 and thence, via e1 and b3, to the zodiac scale on the Front Dial and the lunar phase⁷ mechanism. Our CT confirms the complex structure of axis e that this model entails.

A major aim of this investigation is to set up a data archive to allow noninvasive future research, and access to this will start in 2007. Details will be available on www.antikytheramechanism.gr.

The Antikythera Mechanism shows such great economy and ingenuity of design.

It stands as a witness to the extraordinary technological potential of Ancient Greece, apparently lost within the Roman Empire.

Bibliography

1-Price, D. de S. Gears from the Greeks: The Antikythera Mechanism — A Calendar Computer from ca. 80 BC, Trans Am. Philos. Soc., New Series, 64, Part 7 (reprinted as Science History Publications, NY 1975), (1974)

2-Wright, M.T. Epicyclic Gearing and the Antikythera Mechanism, Part I, Antiquarian Horology, Vol. 27 No. 3, pp. 270279, March (2003)
3-Wright, M.T., Bromley, A. G. and Magkou, E. Simple XRay Tomography and the Antikythera Mechanism, PACT 45 (1995) , Proceedings of the conference Archaeometry in SouthEastern Europe, pp. 531543, April (1991)

4-Wright, M.T. The Antikythera Mechanism: a New Gearing Scheme. Bulletin of the Scientific Instrument Society, No. 85, pp. 27, (2005)
5-Wright, M.T. Epicyclic gearing and the Antikythera Mechanism, Part II. Antiquarian Horology, Vol. 29, No. 1, pp. 5163, September (2005)

6-Wright, M.T. Counting Months and Years: The Upper Back Dial of the Antikythera Mechanism. Bulletin of the Scientific Instrument Society, No. 87, pp. 813, (2005)
7-Wright, M.T. The Antikythera Mechanism and the Early History of the MoonPhase Display, Antiquarian Horology, Volume 29, No.3, March 2006, pp. 319329, (2006)

8-Wright, M.T. Understanding the Antikythera Mechanism, Proceedings 2nd International Conferenceon Ancient Greek Technology, Technical Chamber of Greece, Athens, pp 4960, (2006)

9-Wright, M.T. A Planetarium Display for the Antikythera Mechanism. Horological Journal, Volume 144, No.5, pp. 169173; 144, No.6 p193 (2002)

10-North, J.D. The Fontana History of Astronomy and Cosmology, Fontana Press, (1994)
11-Bromley, A. G. The Antikythera Mechanism, Horological Journal, Vol 132, pp. 412415, (1990)

12-Bromley, A. G. Antikythera: An AustralianMade Greek Icon!, Bassernet, Vol. 2, No. 3, June 1993, Basser Department of Computer Science, University of Sydney, (1993)
13-Freeth, T. The Antikythera Mechanism: 1. Challenging the Classic Research, Mediterranean Archaeology & Decoding the Antikythera Mechanism, published in Nature, Volume 444, Issue 7119, pp. 587-591 (2006). Archaeometry, Vol. 2 No. 1, pp. 2135, (2002)
14-Edmunds, M. and Morgan, P. The Antikythera Mechanism: still a mystery of Greek astronomy?, Astronomy & Geophysics, Vol. 41, pp. 6.106.17, (2000)
15-Toomer, G. J. Ptolemy’s Almagest, translated by G. J. Toomer, with a foreword by Owen Gingerich, Princeton University Press, (1998)
16-Freeth, T. The Antikythera Mechanism: 2. Is it Posidonius’ Orrery?, Mediterranean Archaeology & Archaeometry, Vol. 2 No. 2, pp. 4558, (2002)
17-XTek Systems Ltd, 3D Computed Tomography (2006). http://www.xtek.co.uk/ct/
18-Malzbender, T. and Gelb, D. Polynomial Texture Mapping, HewlettPackard Mobile and Media Systems Laboratory, (2006). http://www.hpl.hp.com/research/ptm/
19-Brooks, M. Tricks of the Light, New Scientist, No 2285, 7 April (2001)
20-Illsley, J.S. http://cma.soton.ac.uk/HistShip/shlect36.htm
21-Britton, J.P. Scientific Astronomy in PreSeleucid Babylon. Chapter in H.D. Galter (ed.), Die Rolle der Astronomie in den Kulturen Mesopotamiens. Graz, (1993)
22-Stephenson, F. R. Historical Eclipses and Earth’s Rotation, Cambridge University Press, (1997)
23-Steele, J. M. Observations and Predictions of Eclipse Times by Early Astronomers, Kluwer Academic Publishers, Dordrecht, ISBN 0792362985, (2000)
24-Steele, J. M. Eclipse Prediction in Mesopotamia, Arch. Hist. Exact Sci. 54, pp. 421454, (2000)
25-Wright, M.T. The Scholar, the Mechanic and the Antikythera Mechanism. Bulletin of the Scientific Instrument Society, No. 80, pp. 411, (2003)
26-Espenak F. NASA’s website on eclipses developed by Fred Espenak. All modern eclipse data and predictions in our work are by Fred Espenak, NASA/GSFC (2005). http://sunearth.gsfc.nasa.gov/eclipse/eclipse.html
27-Chapman, A. Dividing the Circle, J.Wiley, Chichester, (1995)
28-Jones, A. The Adaptation of Babylonian Methods in Greek Numerical Astronomy, Isis, Vol. 82, No. 3, pp. 440453, Sep (1991)