|
PARTE V PRUEBA MATEMÁTICA
Figura 44. Empleando parte de las matemáticas básicas, se pueden hallar los números esenciales del ciclo de las manchas solares:
Reste el segundo número del primero: 2.627 - 1.846 = 781
781 es el número de los períodos de tiempo (bits) hallados por Cotterrell en un ciclo de 68.302 días. Divida los números ya hallados, pero en el orden inverso, por el tiempo de rotación de los campos magnéticos y obtendrá:
Un ciclo tiene 781 bits. Es posible seguir dividiéndolo:
Por este medio, usted puede calcular un ciclo prolongado:
Esto también es igual a lo siguiente (cálculos opuestos):
Gracias a este número, yo pude descifrar el Códice Dresden de los mayas. Por estos cálculos quedaba claro que este era un número esencial del ciclo de las manchas solares.
De ahí que los mayas lo
han incorporado a sus códigos.
Cuando los dividimos por 27, se halla la primera clave:
La diferencia indica qué es lo que buscamos: 962 = 37 x 26. La relación no se detiene en este punto: 27 x 37 = 999
Aparecen dos números importantes a partir de este cálculo: 26 y 37. Más aún, el ciclo magnético de 26 días puede calcularse desde el otro. La serie infinita de 26 es la evidencia.
Esto también es posible al revés:
Si este no es un juego brillante, entonces yo estoy loco.
Lo que sigue es importante en grado sumo: el tema del Códice Dresden es, de hecho, el ciclo de las manchas solares. Muchas personas no se han convencido después de haber leído la decodificación realizada por Maurice Cotterrell. Pero cuando está decodificada correctamente, resulta claro que se refiere al ciclo de las manchas solares. Esto es asombroso porque esta teoría es extremadamente difícil y los astrónomos no tienen noción de su existencia.
Tras de él se ocultan cientos de códigos secretos. Algunos están relacionados con el magnetismo solar y el ciclo de las manchas solares.
Figura 45. Reemplace 584 por 583,02 que es el número exacto del período sinódico de Venus. La diferencia es 0,08. Cuando multiplicamos este último por 2.340, obtenemos: 0,08 x 2.340 = 187,2.
¡¡Este número es
el período del ciclo de las manchas solares!
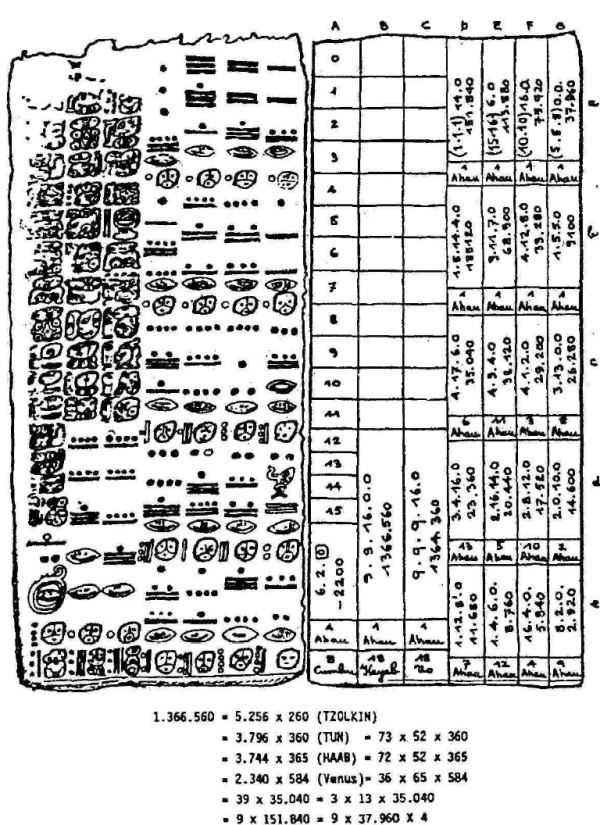
Descifrar el Códice Dresden Dentro del Códice hay dos números:
La diferencia es: 1.366.560 - 1.364.360 = 2.200
Esta serie de números 0,163636363 representa un ciclo completo de 360 grados:
La diferencia entre ambas series de números es:
Dicha solución tiene que ver con una diferencia de 360 grados. Esto es lo que usted ya sabe:
Como código primario tenemos el ciclo de las manchas solares de 187,2 años = 68.328 días.
Cotterell obtuvo un valor de 68.302 días.
El ciclo exacto de las manchas solares es:
Si dividimos esto por 2.200:
¡Usted conoce este número! Ya lo obtuvo antes como un código del ciclo de las manchas solares, ¡pero diez veces mayor!
El valor real es 2,363636. Esto puede comprobarse de la siguiente manera:
Multiplique estos números por 10:
Multiplique los números precedentes por 10:
La resta da el valor correcto:
¡Este es el código primario!
Luego de 2,363636 rotaciones, un campo magnético del Sol alcanza al otro. Además, el código del otro campo magnético puede recuperarse: 3,363636. Esto es relativamente fácil.
Como ya lo sabe de antes, con la división por tres números se puede obtener el código:
Divida 520 por estos números:
Divida las últimas dos series por 2.200:
La diferencia entre el código maya y el real es:
Divida esto por 2.200:
Este código es 10 veces más pequeño y se demuestra de la siguiente manera:
Conclusión: 520 / 220 = 2,363636
Los números de Venus conocidos condujeron a la siguiente revelación:
Los códigos siguientes se encuentran detrás de esto:
Las sumas y las restas confirman la corrección de estos números:
Debemos averiguar más todavía. La siguiente conexión ofrece más revelaciones del antiguo mensaje codificado:
Luego de 87,454545 días, uno de los campos polares alcanza al otro.
Multiplique esto por la rotación de los campos:
Reste 25,297297 del número 26:
Multiplique esto por la rotación del campo del ecuador y obtendrá la rotación del campo en los polos:
Esto se comprueba, restando entre sí los códigos de Venus obtenidos antes:
Este código tiene un cierto significado.
Cuando los valores de los campos magnéticos antes obtenidos se dividen por 10, se concluye lo siguiente:
La serie infinita del número 0,00363636 se encuentra en el mismo orden que en los códigos de Venus.
Para lograrlo, tendrá que adaptar los otros números:
51 se resta el segundo resultado por el primero, se obtiene 22:
La solución del Códice Dresden Los números hallados anteriormente condujeron a la siguiente solución:
Los números 3 y 2 también indican un código:
Vemos una serie infinita con el número 36, por lo tanto, multiplicando 74 y 52 por 36, se obtiene:
Si se divide por las rotaciones de los campos, se halla el próximo código:
Este número también es el resultado de restar de los códigos primarios lo siguiente:
La siguiente división conduce a un código adicional:
El número maya del ciclo largo de la mancha solar también da un código:
Estos números concuerdan con la precesión (vea el Capítulo 16).
Pero, ¡atención!, se trata de una importante evidencia.
El número 1.366.560 del Códice Dresden es igual a:
Se obtiene el mismo número de manera diferente:
260 es un número especial. Es la conexión entre los diferentes calendarios y las rotaciones solares.
El campo ecuatorial viaja cada día:
Ya se obtuvo varias veces el número 0,7027027.
Esto también es igual a:
Luego de 260 días, el campo polar ha viajado 7,027027 rotaciones. La cantidad de grados para este período es:
La cantidad de rotaciones puede calcularse de la siguiente manera:
El campo se encuentra a 0,027027027 rotaciones de su punto de partida. Esto es igual al siguiente número de grados:
Esto significa que el campo está a un día antes de su punto de partida, ó 9,729729 grados. El campo ecuatorial ha realizado diez rotaciones después de 260 días y se encuentra en su punto de partida.
A continuación he descifrado un código que demuestra la rectitud de este principio:
Esto muestra un código para el calendario maya:
Multiplique esto por la cantidad de grados viajados en un día:
Cuando se multiplica 72 por el número de rotaciones de un ciclo en 260 días (razón: 18.720 = 72 x 260), se obtiene el siguiente valor:
Aumente el número en 1.000 veces (razón: los números obtenidos son mayores en la misma proporción):
He aquí una conexión con el número de los mayas:
Reste este valor del número grande obtenido antes:
El resultado es idéntico al primer número, sólo la unidad es diferente. Y esto no termina aquí.
La cantidad de grados que viaja un campo en 72 días también da un código:
Dividido por el número anterior, puede calcularse la cantidad de grados que el otro campo viaja en un día:
Si seguimos con el razonamiento sobre el número del código, se obtiene lo siguiente:
Al cabo de 18.720 días, el campo polar ha viajado 182.140,54054 grados. Esto es 19,459459 grados menos que un círculo completo. El campo ecuatorial se encuentra en su punto de partida.
Conclusión: el campo está 2 x 9,729279 detrás del otro.
Según los mayas, esto puede describirse de la siguiente manera:
Para un ciclo calendario de 18.980 días, obtendremos:
La conexión con el número maya 512.460 (= 1.460 x 351):
Cuando esto se decodifica de la misma manera que antes:
Conclusión: el ciclo de 260 días da una diferencia de 9,729729 grados entre los campos. Luego de 18.980 días, este fenómeno se repite.
El ciclo calendario refleja un ciclo entre el polo solar y
el ecuador solar.
Como se ha demostrado, hay dos números diferentes de esencial importancia en la fundación de la Atlántida. En los cálculos obtenemos dos números fundamentales: 36 y 144. El 36 representa los 360 grados, lo cual significa que en un día, la Tierra cubre un círculo completo.
Esto se relaciona con el segundo número: 144, que representa 1.440.
A continuación se demuestra que esto es correcto:
Como recordará, el número 864 es el primer lapso por el zodíaco. El cálculo de nuestro tiempo es, de hecho, la información que se brinda para calcular la precesión del zodíaco.
Para ayudarlo a recordar, le informo nuevamente cuáles son los cinco números principales que dominaron la fundación de la Atlántida antes del primer cataclismo:
La cantidad de horas por día puede calcularse de tres maneras. Para empezar el primer cálculo, haga la siguiente operación:
Cuando dividimos el zodíaco completo por 360, se obtiene 25.920 - 360 = 72.
También,
También puede demostrarse de qué manera obtuvieron 60 segundos y 60 minutos. Como ya sabe, el número 5.184 es importante:
Al dividir este número por 360 obtenemos:
Una última división da el número de segundos y/o minutos:
Puede hallarse más evidencia en lo siguiente:
¡Este número simboliza la cantidad de grados cubiertos por segundo!
Para calcular la precesión del zodíaco con nuestro propio cálculo del tiempo como punto de partida, se debe seguir la ruta opuesta. En un día hay 24 horas y la Tierra gira 360 grados en el zodíaco. Para dejar que 24 concuerde con los 12 signos del zodíaco, hay que dividir: 12 = 24 / 2. En un día tenemos 2 x 12 horas.
Pero en realidad, esto se corresponde con los seis signos del zodíaco: 12 / 2 = 6.
Si lo multiplicamos con el número de segundos en medio día, obtendremos:
Esto puede demostrarse de la siguiente manera: divida el número de segundos por día por 360 y obtendrá:
Esto significa que nuestro número 259.200 debe dividirse por 10. También puede hacerlo con la cantidad de minutos.
En medio día tenemos 720 minutos:
Aún puede demostrarse que todo esto es correcto, de la siguiente manera:
En el Capítulo 7 descifré un importante código del zodíaco. Me dio
tres números: 2.592; 2.016 y 1.440. Los dos últimos pueden hallarse
también en el cálculo de nuestro tiempo. A los atlantes les
encantaba dividir, multiplicar, sumar y restar, y nosotros estamos
haciendo lo mismo: 24 x 24 = 576.
Luego, hágalo otra vez:
Conclusión: sume el producto de ambos números ¡y obtendrá el número
final!
Ahora, tendría que estar muy ciego para no ver el código. Algo debe dividirse y multiplicarse por 6:
Ambos números son de extrema importancia:
Prueba: 72 representa los 720 minutos. 720 x 2 = 1.440 minutos por día y 36 representa los 360 grados. El número anterior, 5.184, fue obtenido multiplicando por sí mismo el número de minutos en medio día.
Ahora, haga lo mismo para el otro número 144 (144 representa 1.440 minutos).
Prueba: 864 representa 86.400 segundos y 24 representa 24 horas.
La demostración de los atlantes en cuanto a esta proposición es así:
Este último número indica el ciclo completo de
25.920 años (ver: La duración del ciclo zodiacal).
Luego de que la Atlántida pereció, los sobrevivientes se dispersaron por todo el mundo. Basándome en sus números, yo podré demostrar eso.
Para empezar:
Si divide todos los números importantes de los atlantes por 5, obtendrá el siguiente resultado:
El supernúmero 5.184 es divisible por todos los números resultantes, excepto por el 52 y el 73.
Cuando empezamos por las series precedentes, ¡pueden obtenerse importantes números de los mayas!
Si multiplicamos 720 por 200 obtenemos:
Números mayas y sistemas numéricos:
He aquí la primera prueba de que los egipcios y los mayas
originalmente tenían la misma manera de calcular. A continuación
podrá encontrar una evidencia más sólida.
La conexión entre el ciclo de Venus y las series numéricas egipcias
Al dividir un año de 365 días por 360, se obtiene el siguiente número:
Al multiplicarlo por 576, siendo este último un importante número de código como se ha demostrado en otras series, hallamos que: 576 x 1,01388888 = 584 = período de tiempo sideral de Venus. El tiempo sideral de un planeta es el tiempo que tarda para retornar al mismo lugar en el espacio. Aparentemente, los mayas, al igual que los egipcios, trabajaban con este número, dada la sorprendente similitud.
Si dividimos este número por 584:
Antes de continuar, se necesitan algunos cálculos adicionales:
Los mayas decían que la reversión del campo magnético del Sol se produciría después de 20 pasajes de Venus:
Una serie está integrada por 117 pasajes siderales de 584 días. La veracidad de estos datos se comprueba por los siguientes cálculos adicionales:
Hay más evidencia todavía:
Hay más conexiones entre los números mayas y egipcios:
En Egipto, 1.460 era el período del tiempo sideral de un año sotíaco (de Sothis = Sirio). Aquí queda demostrada claramente la conexión con el supernúmero maya. Además, usted sabe que el número 144 era importante en Egipto.
Más datos se basan en el siguiente cálculo:
El número 52 representa a 260 + 52 = 5. Si multiplica el resultado por 18.980, obtendrá:
Cuando se multiplica este último número por 14,4 vuelve a obtenerse el supernúmero maya (1.366.560).
Ahora, divida el número mayor, 18.980 —que era sagrado para los mayas—, por su valor calculado y obtendrá:
Creo que esta evidencia es suficiente para demostrar que existe una
clara conexión entre los mayas y los egipcios. Ciclo de las manchas solares mayas, calculado desde el zodíaco egipcio Previamente ya hemos hallado dos números "especiales", donde 5.184 no es divisible por ellos; estos son el 73 y el 52. Si los multiplica entre sí, obtendrá: 73 x 52 = 3.796.
He aquí un número al que también se arriba cuando se calcula el supernúmero maya de la destrucción.
En este momento, uno claramente puede hablar de una conexión.
El número 1.872 representa el tiempo más corto del zodíaco, siendo el más largo, 2.592 años.
Si multiplica 720 por 1.898, obtendrá:
Este ciclo es demasiado grande y puede demostrarse de la siguiente manera:
Multiplique este último número por 52 y obtendrá el número maya superlargo:
El número 73 puede calcularse del ciclo que es demasiado largo:
Sabemos que la precesión del zodíaco tarda 25.920 años; 26.820 apunta a un número mayor que el necesario y puede calcularse cuánto es el exceso:
Este es el valor del ciclo corto que equivale a 68.328 días. Para referirse a la cuenta superlarga, hay que multiplicar por 20.
Entonces, el período que indica la reversión del campo magnético del Sol es el siguiente:
A continuación le muestro de qué manera tan hermosa puede unirse todo:
Un ciclo corto tiene exactamente 68.302 días. Esto es igual a:
El ciclo demasiado largo es posible calcularlo de la siguiente manera:
Cada 187 años, la cantidad de manchas solares aumenta o disminuye.
Los mayas y los egipcios sabían esto:
Para sus cálculos, utilizaban números "sagrados". Por lo tanto, primero hay que introducirse en su patrón de pensamiento, antes de poder descifrar un código. De varias maneras se obtiene que en sus cálculos cuentan muchas veces 26 días.
He aquí algunos ejemplos:
Réstele a esto los primeros números que obtuvimos:
Divida ambos números entre sí y obtendrá:
Podemos extraer todavía más información de sus "juegos numéricos", de la siguiente manera:
Y finalmente, regresamos por un momento al zodíaco. El ciclo más corto y el más largo se expresan matemáticamente de la siguiente manera:
Otra vez, esto significa que el período corto debe multiplicarse por
20 para calcular la reversión del magnetismo del Sol. Si hay alguien
que todavía dice que no eran extraordinariamente brillantes,
¡debería hacerse examinar la cabeza!
1 N. de la T.: GPS en inglés, Global Positioning System. Es un sistema de satélites, computadoras y receptores, que puede determinar la latitud y longitud de un receptor en la Tierra, calculando la diferencia de tiempo para las señales desde los diferentes satélites hasta el receptor.
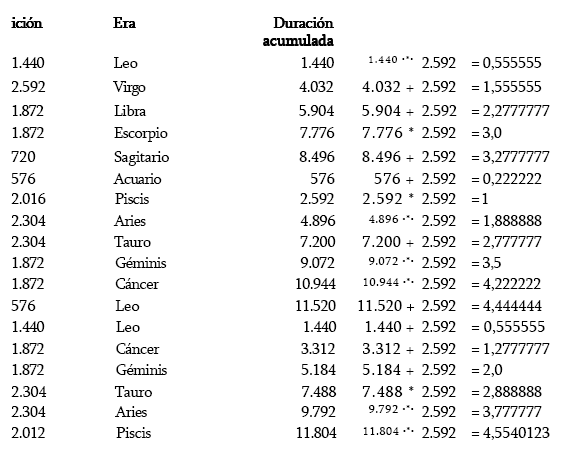
Más códigos secretos del zodíaco de la Atlántida Al enumerar los códigos secretos del zodíaco de la Atlántida hasta la era actual, se obtienen las siguientes series de números:
Con el cálculo de este último número, me topé con un gran interrogante. Los tres cataclismos siguientes tuvieron lugar en una era donde, dividida por 2.492, nos da una serie de números. Primero, ingresé el número 2.012 en mi calculadora de bolsillo, porque la Era de Piscis empezó en el año antes de Cristo. Con esto, llegamos al número 37.724 como el año.
Al dividirlo por 2.592 obtuve:
Entonces intenté con otros números (como 2.002, 2.004, etc.), pero sin ningún resultado. ¡Sólo 2.016 da una serie de números! ¿Cómo se conecta esto con la fecha 2.012?
Hay tres posibilidades:
No obstante, hay más códigos vinculados con estos números.
Al calcular lo mismo, pero empezando desde cada cataclismo, arribamos al siguiente resultado:
Una vez más, destacamos que la fecha esperada no concuerda con las series numéricas.
¿Será esta la mayor catástrofe que jamás
hayamos tenido?
Cálculos del Capítulo 6
Usted ya lo ha comprobado antes, pero ahora lo hará de manera diferente, para que sepa comprender la manera de razonar de los atlantes:
Con los números precedentes, se puede obtener un importante número para completar el código del zodíaco:
Una vez más, destacamos que la fecha esperada no concuerda con las
series numéricas. ¿Será esta la mayor catástrofe que jamás hayamos
tenido?
Este número es especial; con cálculos posteriores obtenemos:
Con esto nos encontramos al final de nuestra historia: Ahora ya ha
hecho un avance en cuanto a la manera de pensar de los
10.368 x 0,25 = 2.592 = 1 /10 ciclo. atlantes. Debo admitir que me
llevó meses comprenderlo, por lo tanto, no espere lograrlo así, en un solo intento. De lo siguiente se puede entender que el ciclo tiene un periodo de 25.920 años:
La siguiente es otra evidencia adicional:
Los egipcios empelaban un ciclo de 25.920 años en sus cálculos. Pero la duración exacta al final es de 25.776. Puede estar seguro de que ellos también sabían esto que puede hallarse al comienzo de su era.
Se trata de lo siguiente:
Al restar 2.448 de 2.592, obtenemos:
Entonces, el cuadrado de 12 tiene que ver con la solución.
Por eso decidí hacer lo opuesto y dividí por 12:
Al restar estos resultados, ¡otra vez se obtiene doce!
El ciclo zodiacal para calcular el final, entonces, es el siguiente:
Traducción: para obtener un ciclo correcto, debemos restar la diferencia entre ambos números del ciclo completo. Se demuestra que esto es válido en otros cálculos adicionales. Por lo tanto, yo utilicé el número 72 que ya había hallado.
Al dividir los dos ciclos por 72, obtuve:
La diferencia arrojó el número dos: 360 - 358 = 2. Si multiplicamos los cocientes de estas dos divisiones, obtenemos:
Entonces, aún debía hacer algo con el número dos.
Una corta multiplicación me dio el resultado que estaba esperando:
Esto está sólo a 17,28 segundos del valor real. Como ya lo he afirmado, deben haber sabido que un año solar tiene 365,2422 días. Su cálculo sólo falla en 0,08 segundos del valor real, es decir, ¡una falla de 0,000000003%!
El tiempo entre los cataclismos anteriores es de 11.520 años (21.312 - 9.972 = 11.520).
Divídalo por el número sagrado 72 (en el año 21.312 a.C, la Tierra giró 72 grados en el zodíaco):
Venus desaparece ocho días después del Sol (584 - 8 = 576).
Un círculo completo tiene 360 grados: 72 + 288 = 360.
Divídalo por 288:
En el Códice Dresden, los mayas emplearon 365 días:
Esto es:
Los mayas conocían el número correcto para Venus, es decir: 583,92:
Reste esto del número hallado antes:
Los mayas sabían que un año tiene 365,242 días, pero con esto se puede demostrar ¡que sabían que un año tiene 365,2422 días!
Reste esto del número hallado antes:
La diferencia es:
Divida esto:
Se puede demostrar que la decodificación es correcta, con el número maya:
Utilizando el mismo método, pueden decodificarse todos los
calendarios mayas.
Después de esto, muchos interrogantes fueron contestados rápidamente. Pronto vi la conexión con el número hallado en el ciclo del zodíaco.
Cuando se resta 72 de 2.664, se obtiene el número de precesión, pero diez veces menor:
Hasta ahora, yo usé dos veces el número 72 y sólo una el 360. Me preguntaba si no habría otra conexión, y sí la había.
Dado que hallé un ciclo de precesión diez veces menor, multipliqué este número por 36:
Sé las tablas de multiplicar hasta 20 x 20, lo cual me ayudó a observar el código de otra manera. Cuando se resta el número de precesión de este número, se obtiene el número menor hallado previamente:
Esto es un décimo de ciclo. ¿Significa que los círculos producen un ciclo que es un diez por ciento más grande? Por cierto que sí; existe investigación que reconoce esta presunción. Cada 68.302 días, una mancha solar transita por su ciclo. En el Capítulo 15 hemos calculado el número de rotaciones de los campos magnéticos que lo utilizan.
Cuando empleamos el método de resta incluido antes, se obtiene lo siguiente:
Dada la excepcional importancia de esta obra, sólo se mencionan los libros relevantes, para que los lectores y los investigadores no pierdan su tiempo inútilmente.
|