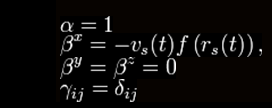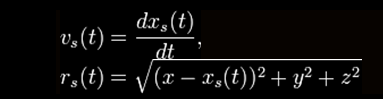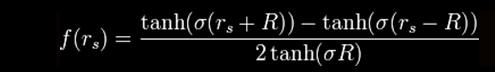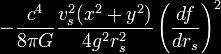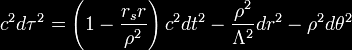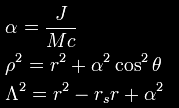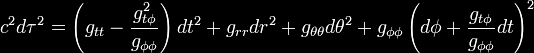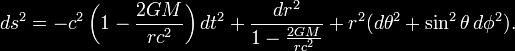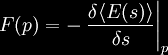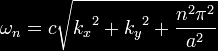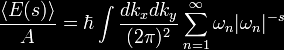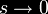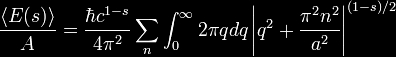|

by Dr. David Lewis Anderson
2008
from
AndersonInstitute Website
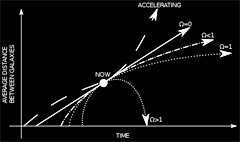
The ability to control time in both a
forward and backwards direction is possible within the laws of our
mathematics and physics. The chart below (click for larger view)
compares ten different technologies an methods.
Key characteristics are identified for
each and described below.
Under each key characteristic is a
column with either a solid or empty circle.
A solid circle indicates a key
characteristic is supported by the indicated technology or method,
an empty circle indicates it is not.
-
"Time Control" indicates whether
travel to future, past, or both are possible.
-
"Matter Transport" is solid if
both matter and information can be transported, empty if
only information can be transported.
-
"Tech Viability" is solid if the
technology or method is viable with present state-of-the-art
technology or within two generations.
-
"Possible Without Exotic
Materials" is solid if materials required are available
today or within two generations.
-
"Relatively Low Input Power" is
solid if time control is achievable within power generation
capabilities available today or within two generations.
The time control technologies and
methods above include the following:
Contents
-
Quantum Tunneling
-
Near-Lightspeed
-
Alcubierre Warp
Drive
-
Faster-than-Light
-
Time-warped Field
-
Circulating
Light Beams
-
Wormholes
-
Cosmic Strings
-
Tipler Cylinder
-
Casimir Effect
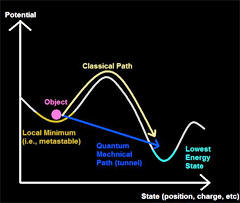
Quantum Tunneling
Quantum Tunneling is an evanescent wave coupling effect that occurs
in quantum mechanics.
The correct wavelength combined with the
proper tunneling barrier makes it possible to pass signals faster
than light, backwards in time.
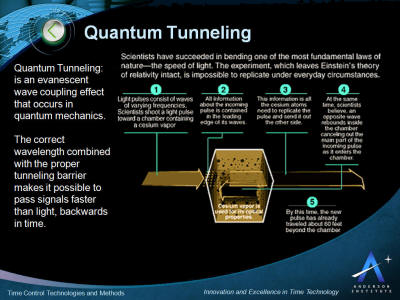
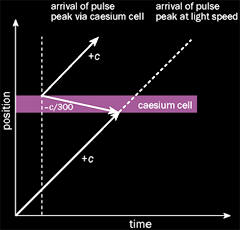
In the diagram above light pulses
consisting of waves of various frequencies are shot toward a 10
centimeter chamber containing cesium vapor.
All information about
the incoming pulse is contained in the leading edge of its waves.
This information is all the cesium atoms need to replicate the pulse
and send it out the other side.
At the same time it is believed an opposite wave rebounds inside the
chamber cancelling out the main part of the incoming pulse as it
enters the chamber. By this time the new pulse, moving faster than
the speed of light, has traveled about 60 feet beyond the chamber.
Essentially the pulse has left the chamber before it finished
entering, traveling backwards in time.
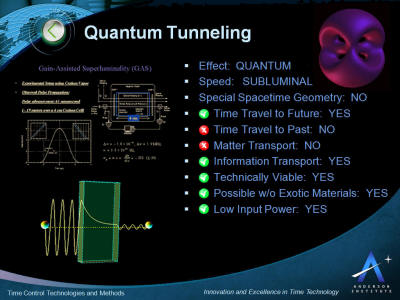
The key characteristics of the application of quantum tunneling for
time control and time travel are presented in the picture below.
This is followed by more detail describing the phenomenon below.
Wave-mechanical tunneling (also called
quantum-mechanical tunneling, quantum tunneling, and the tunnel
effect) is an evanescent wave coupling effect that occurs in the
context of quantum mechanics because the behavior of particles is
governed by Schrödinger's wave-equation.
All wave equations exhibit
evanescent wave coupling effects if the conditions are right. Wave
coupling effects mathematically equivalent to those called
"tunneling" in quantum mechanics can occur with Maxwell's
wave-equation (both with light and with microwaves), and with the
common non-dispersive wave-equation often applied (for example) to
waves on strings and to acoustics.
For these effects to occur there must be a situation where a thin
region of "medium type 2" is sandwiched between two regions of
"medium type 1", and the properties of these media have to be such
that the wave equation has "traveling-wave" solutions in medium type
1, but "real exponential solutions" (rising and falling) in medium
type 2.
In optics, medium type 1 might be glass, medium type 2 might
be vacuum. In quantum mechanics, in connection with motion of a
particle, medium type 1 is a region of space where the particle
total energy is greater than its potential energy, medium type 2 is
a region of space (known as the "barrier") where the particle total
energy is less than its potential energy.
If conditions are right, amplitude from a traveling wave, incident
on medium type 2 from medium type 1, can "leak through" medium type
2 and emerge as a traveling wave in the second region of medium type
1 on the far side. If the second region of medium type 1 is not
present, then the traveling wave incident on medium type 2 is
totally reflected, although it does penetrate into medium type 2 to
some extent.
Depending on the wave equation being used, the leaked
amplitude is interpreted physically as traveling energy or as a
traveling particle, and, numerically, the ratio of the square of the
leaked amplitude to the square of the incident amplitude gives the
proportion of incident energy transmitted out the far side, or (in
the case of the Schrödinger equation) the probability that the
particle "tunnels" through the barrier.
Quantum Tunneling Introduction
Quantum Tunneling
The scale on which these "tunneling-like phenomena" occur depends on
the wavelength of the traveling wave.
For electrons the thickness of
"medium type 2" (called in this context "the tunneling barrier") is
typically a few nanometers; for alpha-particles tunneling out of a
nucleus the thickness is very much less; for the analogous
phenomenon involving light the thickness is very much greater.
With Schrödinger's wave-equation, the characteristic that defines
the two media discussed above is the kinetic energy of the particle
if it is considered as an object that could be located at a point.
In medium type 1 the kinetic energy would be positive, in medium
type 2 the kinetic energy would be negative. There is no
inconsistency in this, because particles cannot physically be
located at a point: they are always spread out ("delocalized") to
some extent, and the kinetic energy of the delocalized object is
always positive.
What is true is that it is sometimes mathematically convenient to
treat particles as behaving like points, particular in the context
of Newton's Second Law and classical mechanics generally. In the
past, people thought that the success of classical mechanics meant
that particles could always and in all circumstances be treated as
if they were located at points.
But there never was any convincing
experimental evidence that this was true when very small objects and
very small distances are involved, and we now know that this
viewpoint was mistaken. However, because it is still traditional to
teach students early in their careers that particles behave like
points, it sometimes comes as a big surprise for people to discover
that it is well established that traveling physical particles always
physically obey a wave-equation (even when it is convenient to use
the mathematics of moving points).
Clearly, a hypothetical classical
point particle analyzed according to Newton's Laws could not enter a
region where its kinetic energy would be negative. But, a real
delocalized object, that obeys a wave-equation and always has
positive kinetic energy, can leak through such a region if
conditions are right.
An approach to tunneling that avoids mention
of the concept of "negative kinetic energy" is set out below in the
section on "Schrödinger equation tunneling basics".
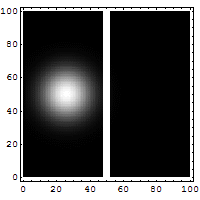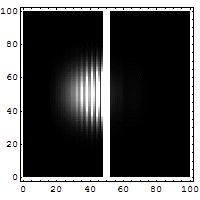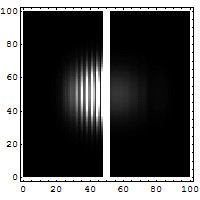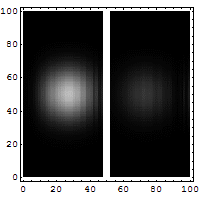
Reflection and
tunneling of an electron
wave packet directed at a potential barrier.
The bright spot moving to the left is the
reflected part of the wave packet. A very
dim spot can be seen moving to the right
of the barrier. This is the small fraction of
the wave packet that tunnels through the
classically forbidden barrier. Also notice
the interference fringes between the
incoming and reflected waves.
An electron approaching a barrier has to
be represented as a wave-train.
This wave-train can sometimes be
quite long – electrons in some materials can be 10 to 20 nm long.
This makes animations difficult. If it were legitimate to represent
the electron by a short wave-train, then tunneling could be
represented as in the animation alongside.
It is sometimes said that tunneling occurs only in quantum
mechanics. Unfortunately, this statement is a bit of linguistic
conjuring trick. As indicated above, "tunneling-type"
evanescent-wave phenomena occur in other contexts too. But, until
recently, it has only been in quantum mechanics that evanescent wave
coupling has been called "tunneling". (However, there is an
increasing tendency to use the label "tunneling" in other contexts
too, and the names "photon tunneling" and "acoustic tunneling" are
now used in the research literature.)
With regards to the mathematics of tunneling, a special problem
arises. For simple tunneling-barrier models, such as the rectangular
barrier, the Schrödinger equation can be solved exactly to give the
value of the tunneling probability (sometimes called the
"transmission coefficient").
Calculations of this kind make the
general physical nature of tunneling clear.
One would also like to
be able to calculate exact tunneling probabilities for barrier
models that are physically more realistic. However, when appropriate
mathematical descriptions of barriers are put into the Schrödinger
equation, then the result is an awkward non-linear differential
equation. Usually, the equation is of a type where it is known to be
mathematically impossible in principle to solve the equation exactly
in terms of the usual functions of mathematical physics, or in any
other simple way.
Mathematicians and mathematical physicists have
been working on this problem since at least 1813, and have been able
to develop special methods for solving equations of this kind
approximately. In physics these are known as "semi-classical" or
"quasi-classical" methods. A common semi-classical method is the
so-called WKB approximation (also known as the "JWKB
approximation").
The first known attempt to use such methods to
solve a tunneling problem in physics was made in 1928, in the
context of field electron emission.
It is sometimes considered that
the first people to get the mathematics of applying this kind of
approximation to tunneling fully correct (and to give reasonable
mathematical proof that they had done so) were N. Fröman and P.O.
Fröman, in 1965. Their complex ideas have not yet made it into
theoretical-physics textbooks, which tend to give simpler (but
slightly more approximate) versions of the theory.
An outline of one
particular semi-classical method is given below.
Three notes may be helpful. In general,
students taking physics courses in quantum mechanics are presented
with problems (such as the quantum mechanics of the hydrogen atom)
for which exact mathematical solutions to the Schrödinger equation
exist.
Tunneling through a realistic barrier is a reasonably basic
physical phenomenon. So it is sometimes the first problem that
students encounter where it is mathematically impossible in
principle to solve the Schrödinger equation exactly in any simple
way. Thus, it may also be the first occasion on which they encounter
the "semi-classical-method" mathematics needed to solve the
Schrödinger equation approximately for such problems.
Not
surprisingly, this mathematics is likely to be unfamiliar, and may
feel "odd". Unfortunately, it also comes in several different
variants, which doesn't help.
Also, some accounts of tunneling seem to be written from a
philosophical viewpoint that a particle is "really" point-like, and
just has wave-like behavior. There is very little experimental
evidence to support this viewpoint. A preferable philosophical
viewpoint is that the particle is "really" delocalized and
wave-like, and always exhibits wave-like behavior, but that in some
circumstances it is convenient to use the mathematics of moving
points to describe its motion. This second viewpoint is used in this
section.
The precise nature of this wave-like behavior is, however,
a much deeper matter, beyond the scope of this article on tunneling.
Although the phenomenon under discussion here is usually called
"quantum tunneling" or "quantum-mechanical tunneling", it is the
wave-like aspects of particle behavior that are important in
tunneling theory, rather than effects relating to the quantization
of the particle's energy states.
For this reason, some writers
prefer to call the phenomenon "wave-mechanical tunneling.
History

George Gamow
By 1928, George Gamow had solved the theory of the alpha decay of a
nucleus via tunneling.
Classically, the particle is confined to the
nucleus because of the high energy requirement to escape the very
strong potential. Under this system, it takes an enormous amount of
energy to pull apart the nucleus. In quantum mechanics, however,
there is a probability the particle can tunnel through the potential
and escape. Gamow solved a model potential for the nucleus and
derived a relationship between the half-life of the particle and the
energy of the emission.
Alpha decay via tunneling was also solved concurrently by Ronald
Gurney and Edward Condon. Shortly thereafter, both groups considered
whether particles could also tunnel into the nucleus.
After attending a seminar by Gamow, Max Born recognized the
generality of quantum-mechanical tunneling. He realized that the
tunneling phenomenon was not restricted to nuclear physics, but was
a general result of quantum mechanics that applies to many different
systems.
Today the theory of tunneling is even applied to the early
cosmology of the universe.
Quantum tunneling was later applied to
other situations, such as the cold emission of electrons, and
perhaps most importantly semiconductor and superconductor physics.
Phenomena such as field emission, important to flash memory, are
explained by quantum tunneling. Tunneling is a source of major
current leakage in Very-large-scale integration (VLSI) electronics,
and results in the substantial power drain and heating effects that
plague high-speed and mobile technology.
Another major application is in electron-tunneling microscopes which
can resolve objects that are too small to see using conventional
microscopes. Electron tunneling microscopes overcome the limiting
effects of conventional microscopes (optical aberrations, wavelength
limitations) by scanning the surface of an object with tunneling
electrons.
Quantum tunneling has been shown to be a mechanism used by enzymes
to enhance reaction rates. It has been demonstrated that enzymes use
tunneling to transfer both electrons and nuclei such as hydrogen and
deuterium.
It has even been shown, in the enzyme glucose oxidase,
that oxygen nuclei can tunnel under physiological conditions.
Back to Contents
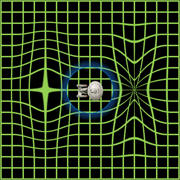
Near-Lightspeed Travel
Near-Lightspeed Travel has the ability to significantly dilate time,
sending an accelerating traveler rapidly forward in time relative to
those left behind before her travel.
The closer to the speed of
light, the further into the future the travel.

The key characteristics of the
application of near-lightspeed travel for time control and time
travel are presented in the picture below.
This is followed by more
detail describing the effect below.

Back to Contents
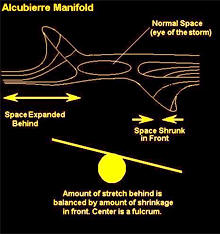
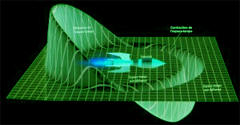
Alcubierre Warp Drive
An Alcubierre Warp Drive stretches spacetime in a wave causing the
fabric of space ahead of a spacecraft to contract and the space
behind it to expand.
The ship can ride the wave to accelerate to
high speeds and time travel.
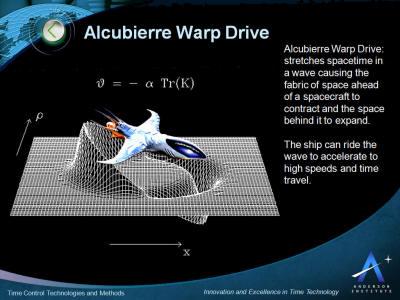
The Alcubierre drive, also known as the
Alcubierre metric or Warp Drive, is a mathematical model of a
spacetime exhibiting features reminiscent of the fictional "warp
drive" from Star Trek, which can travel "faster than light"
(although not in a local sense - see below).
The key characteristics of the application of Alcubierre warp drives
for time control and time travel are presented in the picture below.
This is followed by more detail describing the effect below.

Alcubierre Warp Drive Description
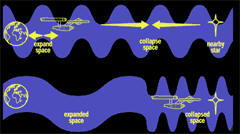
In 1994, the Mexican physicist Miguel
Alcubierre proposed a method of stretching space in a wave which
would in theory cause the fabric of space ahead of a spacecraft to
contract and the space behind it to expand.
The ship would ride this
wave inside a region known as a warp bubble of flat space. Since the
ship is not moving within this bubble, but carried along as the
region itself moves, conventional relativistic effects such as time
dilation do not apply in the way they would in the case of a ship
moving at high velocity through flat spacetime.
Also, this method of
travel does not actually involve moving faster than light in a local
sense, since a light beam within the bubble would still always move
faster than the ship; it is only "faster than light" in the sense
that, thanks to the contraction of the space in front of it, the
ship could reach its destination faster than a light beam restricted
to travelling outside the warp bubble.
Thus, the Alcubierre drive
does not contradict the conventional claim that relativity forbids a
slower-than-light object to accelerate to faster-than-light speeds.
Alcubierre Metric

The Alcubierre Metric defines the
so-called warp drive spacetime.
This is a Lorentzian manifold which,
if interpreted in the context of general relativity, exhibits
features reminiscent of the warp drive from Star Trek: a warp bubble
appears in previously flat spacetime and moves off at effectively
superluminal speed. Inhabitants of the bubble feel no inertial
effects. The object(s) within the bubble are not moving (locally)
faster than light, instead, the space around them shifts so that the
object(s) arrives at its destination faster than light would in
normal space.
Alcubierre chose a specific form for the function f, but other
choices give a simpler spacetime exhibiting the desired "warp drive"
effects more clearly and simply.
Mathematics of the Alcubierre drive
Using the 3+1 formalism of general relativity, the spacetime is
described by a foliation of space-like hypersurfaces of constant
coordinate time t. The general form of the Alcubierre metric is:
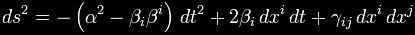
where α is the lapse function that gives
the interval of proper time between nearby hypersurfaces, βI is the
shift vector that relates the spatial coordinate systems on
different hypersurfaces and γij is a positive definite metric on
each of the hypersurfaces.
The particular form that Alcubierre
studied is defined by:
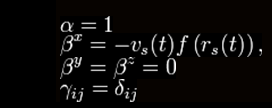
...where,
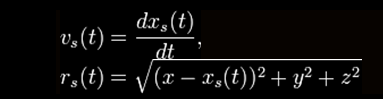
...and,
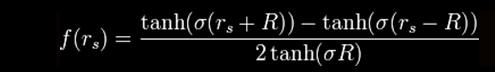
...with R > 0 and σ > 0 arbitrary
parameters. Alcubierre's specific form of the metric can thus be
written;
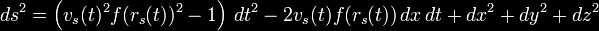
With this particular form of the metric,
it can be shown that the energy density measured by observers whose
4-velocity is normal to the hypersurfaces is given by
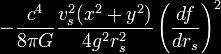
where g is the determinant of the metric
tensor. Thus, as the energy density is negative, one needs exotic
matter to travel faster than the speed of light.
The existence of
exotic matter is not theoretically ruled out, the Casimir effect and
the accelerating universe both lending support to the proposed
existence of such matter.

However, generating enough exotic matter
and sustaining it to perform feats such as faster-than-light travel
(and also to keep open the 'throat' of a wormhole) is thought to be
impractical.
Low has argued that within the context of general
relativity, it is impossible to construct a warp drive in the
absence of exotic matter.
It is generally believed that a consistent
theory of quantum gravity will resolve such issues once and for all.
Physics of the Alcubierre drive
For those familiar with the effects of
special relativity, such as Lorentz contraction and time dilation,
the Alcubierre metric has some apparently peculiar aspects.
In
particular, Alcubierre has shown that even when the ship is
accelerating, it travels on a free-fall geodesic. In other words, a
ship using the warp to accelerate and decelerate is always in free
fall, and the crew would experience no accelerational g-forces.
Enormous tidal forces would be present near the edges of the
flat-space volume because of the large space curvature there, but by
suitable specification of the metric, these would be made very small
within the volume occupied by the ship.
The original warp drive metric, and simple variants of it, happen to
have the ADM form which is often used in discussing the initial
value formulation of general relativity. This may explain the
widespread misconception that this spacetime is a solution of the
field equation of general relativity. Metrics in ADM form are
adapted to a certain family of inertial observers, but these
observers are not really physically distinguished from other such
families.
Alcubierre interpreted his "warp bubble" in terms of a
contraction of "space" ahead of the bubble and an expansion behind.
But this interpretation might be misleading, since the contraction
and expansion actually refers to the relative motion of nearby
members of the family of ADM observers.
In general relativity, one often first specifies a plausible
distribution of matter and energy, and then finds the geometry of
the spacetime associated with it; but it is also possible to run the
Einstein field equations in the other direction, first specifying a
metric and then finding the energy-momentum tensor associated with
it, and this is what Alcubierre did in building his metric.
This
practice means that the solution can violate various energy
conditions and require exotic matter.
The need for exotic matter
leads to questions about whether it is actually possible to find a
way to distribute the matter in an initial spacetime which lacks a
"warp bubble" in such a way that the bubble will be created at a
later time. Yet another problem is that, according to Serguei
Krasnikov, it would be impossible to generate the bubble without
being able to force the exotic matter to move at locally FTL speeds,
which would require the existence of tachyons.
Some methods have
been suggested which would avoid the problem of tachyonic motion,
but would probably generate a naked singularity at the front of the
bubble.
Difficulties
Significant problems with the metric of
this form stem from the fact that all known warp drive spacetimes
violate various energy conditions.
It is true that certain
experimentally verified quantum phenomena, such as the Casimir
effect, when described in the context of the quantum field theories,
lead to stress-energy tensors which also violate the energy
conditions and so one might hope that Alcubierre type warp drives
could perhaps be physically realized by clever engineering taking
advantage of such quantum effects.
However, if certain quantum
inequalities conjectured by Ford and Roman hold, then the energy
requirements for some warp drives may be absurdly gigantic, e.g. the
energy -1067gram equivalent might be required to transport a small
spaceship across the Milky Way galaxy. This is orders of magnitude
greater than the mass of the universe.
Counterarguments to these
apparent problems have been offered, but not everyone is convinced
they can be overcome.
Chris Van Den Broeck, in 1999, has tried
to address the potential issues.
By contracting the 3+1 dimensional
surface area of the 'bubble' being transported by the drive, while
at the same time expanding the 3 dimensional volume contained
inside, Van Den Broeck was able to reduce the total energy needed to
transport small atoms to less than 3 solar masses. Later, by
slightly modifying the Van Den Broeck metric, Krasnikov reduced the
necessary total amount of negative energy to a few milligrams.
Krasnikov proposed that, if tachyonic matter could not be found or
used, then a solution might be to arrange for masses along the path
of the vessel to be set in motion in such a way that the required
field was produced. But in this case the Alcubierre Drive vessel is
not able to go dashing around the galaxy at will.
It is only able to
travel routes which, like a railroad, have first been equipped with
the necessary infrastructure.

Miguel Alcubierre
The pilot inside the bubble is causally disconnected with its walls
and cannot carry out any action outside the bubble.
However, it is
necessary to place devices along the route in advance, and since the
pilot cannot do this while "in transit", the bubble cannot be used
for the first trip to a distant star. In other words, to travel to
Vega (which is 26 light-years from the Earth) one first has to
arrange everything so that the bubble moving toward Vega with a
superluminal velocity would appear and these arrangements will
always take more than 26 years.
Coule has argued that schemes such as the one proposed by Alcubierre
are not feasible because the matter to be placed on the road
beforehand has to be placed at superluminal speed. Thus, according
to Coule, an Alcubierre Drive is required in order to build an
Alcubierre Drive. Since none have been proven to exist already then
the drive is impossible to construct, even if the metric is
physically meaningful.
Coule argues that an analogous objection will
apply to any proposed method of constructing an Alcubierre Drive.
Back to Contents
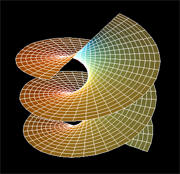
Faster-than-Light Travel
Faster-than-Light Travel is an interesting and controversial
subject. According to special relativity anything that could travel
faster-than-light would move backward in time.
As the same time,
special relativity states that this would require infinite energy.

Faster-than-light (also superluminal or
FTL) communications and travel refer to the propagation of
information or matter faster than the speed of light.
Under the
special theory of relativity, a particle (that has mass) with
subluminal velocity needs infinite energy to accelerate to the speed
of light, although special relativity does not forbid the existence
of particles that travel faster than light at all times.
On the other hand, what some physicists refer to as "apparent" or
"effective" FTL is the hypothesis that unusually distorted regions
of spacetime might permit matter to reach distant locations faster
than what it would take light in the "normal" route (though still
moving subluminally through the distorted region).
Apparent FTL is not excluded by general relativity. Examples of
apparent FTL proposals are the Alcubierre drive and the traversable
wormhole, although the physical plausibility of these solutions is
uncertain.
The key characteristics of the application of faster-than-light
travel for time control and time travel are presented in the picture
below.
This is followed by more detail describing the effect below.

Outside of mainstream physics, others
have speculated on mechanisms that might allow FTL travel to be
achieved, often relying on new conjectures of physics of their own
invention, but their ideas have not gained significant acceptance in
the physics research community.
Fictional depictions of superluminal
travel and the mechanisms of achieving it are also a staple of the
science fiction genre.
Travel

In the context of this article, FTL is
transmitting information or matter faster than c, a constant equal
to the speed of light in a vacuum, 299,792,458 meters per second, or
about 186,282 miles per second.
This is not quite the same as
traveling faster than light, since:
-
Some processes propagate faster than c, but cannot carry
information.
-
Light travels at speed c/n when not in a vacuum but traveling
through a medium with refractive index = n (causing refraction), and
in some materials other particles can travel faster than c/n (but
still slower than c), leading to Cherenkov radiation.
Neither of these phenomena violates special relativity or creates
problems with causality, and thus neither qualifies as FTL as
described here.
Possibility

Faster-than-light communication is, by
Einstein's theory of relativity, equivalent to time travel.
According to Einstein's theory of special relativity, what we
measure as the speed of light in a vacuum is actually the
fundamental physical constant c. This means that all observers,
regardless of their relative velocity, will always measure zero-mass
particles such as photons traveling at c in a vacuum. This result
means that measurements of time and velocity in different frames are
no longer related simply by constant shifts, but are instead related
by Poincaré transformations.
These transformations have important
implications:
-
The relativistic momentum of a massive particle would increase
with speed in such a way that at the speed of light an object would
have infinite momentum.
-
To accelerate an object of non-zero rest mass to c would require
infinite time with any finite acceleration, or infinite acceleration
for a finite amount of time.
-
Either way, such acceleration requires infinite energy. Going
beyond the speed of light in a homogeneous space would hence require
more than infinite energy, which is not generally considered to be a
sensible notion.
-
Some observers with sub-light relative motion will disagree about
which occurs first of any two events that are separated by a
space-like interval. In other words, any travel that is
faster-than-light will be seen as traveling backwards in time in
some other, equally valid, frames of reference, or need to assume
the speculative hypothesis of possible Lorentz violations at a
presently unobserved scale (for instance the Planck scale).
Therefore any theory which permits "true" FTL also has to cope with
time travel and all its associated paradoxes, or else to assume the
Lorentz invariance to be a symmetry of thermodynamical statistical
nature (hence a symmetry broken at some presently unobserved scale).
-
While Special and general relativity do not allow superluminal
speeds locally, non-local means may be possible, which means moving
with space rather than moving through space.
Justifications
Despite the established conclusion that relativity precludes FTL
travel, some have proposed ways to justify FTL behavior:
Radically Curve Spacetime Using Slip String
Drive

There is one way that doesn't violate
Relativity. Andrew L. Bender's Slip String Drive.
Bender proposes
traveling by completely isolating a region of spacetime from the
rest of our universe using Einstein's gravity waves. These
compression waves of spacetime are generated by a ship, which emits
them from its hull in all directions until it is completely isolated
from the rest of our universe. Then, by emitting more gravity waves
behind the ship, it stretches out its isolated bubble into an
egg-shape, causing external spacetime to squeeze in on the bubble
unevenly, propelling the craft forward at speeds no longer limited
by relativity.
Time passes normally within the isolated region,
eliminating the possibility of paradox or time travel.
Ignore special relativity
This option is popular particularly in
science fiction. However, empirical and theoretical evidence
strongly supports Einstein's theory of special relativity as the
correct description of high-speed motion, which generalizes the more
familiar Galilean relativity, which is actually an approximation at
conventional (much less than c) speeds.
Similarly, general
relativity is an overwhelmingly supported and experimentally
verified theory of gravitation, except in the regime of very high
energy densities over very short distances, where an
as-yet-undeveloped theory of quantum gravity is necessary. Special
relativity, however, is incorporated easily into quantum field
theories.
Therefore, even in the broader contexts of general
relativity and quantum mechanics, conventional acceleration from
subluminal to superluminal speeds is not possible.
Faster light (Casimir vacuum and
quantum tunneling)
Einstein's equations of special
relativity postulate that the speed of light in a vacuum is
invariant in inertial frames.
That is, it will be the same from any
frame of reference moving at a constant speed. The equations do not
specify any particular value for the speed of the light, which is an
experimentally determined quantity for a fixed unit of length.
Since
1983, the unit of length (the meter) has been defined using the
speed of light.

Casimir Vacuum
Force
The experimental determination has been made in vacuum.
However, the
vacuum we know is not the only possible vacuum which can exist. The
vacuum has energy associated with it, called the vacuum energy. This
vacuum energy can perhaps be changed in certain cases. When vacuum
energy is lowered, light itself has been predicted to go faster than
the standard value 'c'. This is known as the Scharnhorst effect.
Such a vacuum can be produced by bringing two perfectly smooth metal
plates together at near atomic diameter spacing. It is called a Casimir vacuum. Calculations imply that light will go faster in such
a vacuum by a minuscule amount: a photon traveling between two
plates that are 1 micrometer apart would increase the photon's speed
by only about one part in 1036.
Accordingly there has as yet been no
experimental verification of the prediction. A recent analysis
argued that the Scharnhorst effect cannot be used to send
information backwards in time with a single set of plates since the
plates' rest frame would define a "preferred frame" for FTL
signaling.
However, with multiple pairs of plates in motion relative
to one another the authors noted that they had no arguments that
could "guarantee the total absence of causality violations", and
invoked Hawking's speculative chronology protection conjecture which
suggests that feedback loops of virtual particles would create
"uncontrollable singularities in the renormalized quantum
stress-energy" on the boundary of any potential time machine, and
thus would require a theory of quantum gravity to fully analyze.
Other authors argue that Scharnhorst's original analysis which
seemed to show the possibility of faster-than-c signals involved
approximations which may be incorrect, so that it is not clear
whether this effect could actually increase signal speed at all.
The physicists Günter Nimtz and Alfons Stahlhofen, of the University
of Koblenz, claim to have violated relativity experimentally by
transmitting photons faster than the speed of light. They say they
have conducted an experiment in which microwave photons - relatively
low energy packets of light - travelled "instantaneously" between a
pair of prisms that had been moved up to 3 ft apart, using a
phenomenon known as quantum tunneling.
Nimtz told New Scientist
magazine:
"For the time being, this is the only violation of special
relativity that I know of."
However, other physicists say that this
phenomenon does not allow information to be transmitted faster than
light.
Aephraim Steinberg, a quantum optics expert at the University
of Toronto, Canada, uses the analogy of a train traveling from
Chicago to New York, but dropping off train cars at each station
along the way, so that the center of the train moves forward at each
stop; in this way, the speed of the center of the train exceeds the
speed of any of the individual cars.
Give up causality
Another approach is to accept special
relativity, but to posit that mechanisms allowed by general
relativity (e.g., wormholes) will allow traveling between two points
without going through the intervening space.
While this gets around
the infinite acceleration problem, it still would lead to closed timelike curves (i.e., time travel) and causality violations.
Causality is not required by special or general relativity, but is
nonetheless generally considered a basic property of the universe
that cannot be sensibly dispensed with. Because of this, most
physicists expect (or perhaps hope) that quantum gravity effects
will preclude this option.
An alternative is to conjecture that,
while time travel is possible, it never leads to paradoxes; this is
the Novikov self-consistency principle.
An important point to note is that in general relativity it is
possible for objects to be moving apart faster than light because of
the expansion of the universe, in some reasonable choice of
cosmological coordinates.
This is understood to be due to the
expansion of the space between the objects, and general relativity
still reduces to special relativity in a "local" sense, meaning that
two objects passing each other in a small local region of spacetime
cannot have a relative velocity greater than c, and will move more
slowly than a light beam passing through the region.
Give up (absolute) relativity
Because of the strong
empirical support for special relativity, any modifications to it
must necessarily be quite subtle and difficult to measure.
The
best-known attempt is doubly-special relativity, which posits that
the Planck length is also the same in all reference frames, and is
associated with the work of Giovanni Amelino-Camelia and João
Magueijo.
One consequence of this theory is a variable speed of
light, where photon speed would vary with energy, and some zero-mass
particles might possibly travel faster than c. However, even if this
theory is accurate, it is still very unclear whether it would allow
information to be communicated, and appears not in any case to allow
massive particles to exceed c.
There are speculative theories that claim inertia is produced by the
combined mass of the universe (e.g., Mach's principle), which
implies that the rest frame of the universe might be preferred by
conventional measurements of natural law.
If confirmed, this would
imply special relativity is an approximation to a more general
theory, but since the relevant comparison would (by definition) be
outside the observable universe, it is difficult to imagine (much
less construct) experiments to test this hypothesis.
Non-physical realms

A very popular option in space opera is
to assume the existence of some other realm (typically called
hyperspace, subspace, or slipspace) which is accessible from this
universe, in which the laws of relativity are usually distorted,
bent, or nonexistent, facilitating rapid transport between distant
points in this universe, sometimes with acceleration differences -
that is, not requiring as much energy or thrust to go faster.
To
accomplish rapid transport between points in hyperspace/subspace,
special relativity is often assumed not to apply in this other
realm, or that the speed of light is higher. Another solution is to
posit that distant points in the mundane universe correspond to
points that are close together in hyperspace.
This method of faster-than-light travel does not correspond to
anything seriously proposed by mainstream science.
Space-time distortion

Although the theory of special
relativity forbids objects to have a relative velocity greater than
light speed, and general relativity reduces to special relativity in
a local sense (in small regions of spacetime where curvature is
negligible), general relativity does allow the space between distant
objects to expand in such a way that they have a "recession
velocity" which exceeds the speed of light, and it is thought that
galaxies which are at a distance of more than about 14 billion light
years from us today have a recession velocity which is faster than
light.
Miguel Alcubierre theorized that it would be possible to
create an Alcubierre drive, in which a ship would be enclosed in a
"warp bubble" where the space at the front of the bubble is rapidly
contracting and the space at the back is rapidly expanding, with the
result that the bubble can reach a distant destination much faster
than a light beam moving outside the bubble, but without objects
inside the bubble locally traveling faster than light.
However,
several objections raised against the Alcubierre drive appear to
rule out the possibility of actually using it in any practical
fashion. Another possibility predicted by general relativity is the
traversable wormhole, which could create a shortcut between
arbitrarily distant points in space.
As with the Alcubierre drive,
travelers moving through the wormhole would not locally move faster
than light which travels through the wormhole alongside them, but
they would be able to reach their destination (and return to their
starting location) faster than light traveling outside the wormhole.
Dr. Gerald Cleaver, associate professor of physics at Baylor
University, and Richard Obousy, a Baylor graduate student, theorize
that by manipulating the extra spatial dimensions of string theory
around a spaceship with an extremely large amount of energy, it
would create a “bubble” that could cause the ship to travel faster
than the speed of light. To create this bubble, the physicists
believe manipulating the 10th spatial dimension would alter the dark
energy in three large spatial dimensions: height, width and length.
Cleaver said positive dark energy is currently responsible for
speeding up the expansion rate of our universe as time moves on.
Heim theory
In 1977, a controversial paper on Heim
theory theorized that it may be possible to travel faster than light
by using magnetic fields to enter a higher-dimensional space, and
the paper received some media attention in January 2006.
However,
due to the many unproven assumptions in the paper, there have been
few serious attempts to conduct further experiments.
Quantized space and time
As given by the Planck
length, there is a minimum amount of 'space' that can exist in this
universe (1.616×10−35 meters).
This limit can be used to determine a
minimum time quantization of 5.391×10−44 seconds, which corresponds
to a beam of light with a wavelength approaching the Planck length.
This means that there is a physical limit to how much blue shift a
beam of light can endure. According to general relativity there is
no limit to this shift, and an infinitesimally small space can
exist, but according to well accepted quantum theory these limits do
exist.
This is precisely what happens towards the center of a black hole;
the incoming light becomes blue shifted past the Planck length as it
approaches the region of discontinuity within our universe. The
argument is: if a black hole with finite mass can create such a
discontinuity in the fabric of space and time, why would people be
unable to do the same thing using a finite amount of energy and
acceleration?
(According to general relativity, the space-time
distortions caused by gravity are fundamentally identical to
space-time distortions caused simply by accelerating your reference
frame).
Tachyons
In special relativity, while it is
impossible to accelerate an object to the speed of light, or for a
massive object to move at the speed of light, it is not impossible
for an object to exist which always moves faster than light.
The
hypothetical elementary particles that have this property are called
tachyons. Their existence has neither been proven nor disproven, but
even so, attempts to quantize them show that they may not be used
for faster-than-light communication.
Physicists sometimes regard the
existence of mathematical structures similar to Tachyons arising
from theoretical models and theories as signs of an inconsistency or
that the theory needs further refining.
General relativity
General relativity was developed after
special relativity to include concepts like gravity.
It maintains
the principle that no object can accelerate to the speed of light in
the reference frame of any coincident observer. However, it permits
distortions in spacetime that allow an object to move faster than
light from the point of view of a distant observer. One such
distortion is the Alcubierre drive, which can be thought of as
producing a ripple in spacetime that carries an object along with
it.
Another possible system is the wormhole, which connects two
distant locations as though by a shortcut. Both distortions would
need to create a very strong curvature in a highly localized region
of space-time and their gravity fields would be immense. To
counteract the unstable nature, and prevent the distortions from
collapsing under their own 'weight', one would need to introduce
hypothetical exotic matter or negative energy.
General relativity also agrees that any technique for
faster-than-light travel could also be used for time travel. This
raises problems with causality. Many physicists believe that the
above phenomena are in fact impossible, and that future theories of
gravity will prohibit them.
One theory states that stable wormholes
are possible, but that any attempt to use a network of wormholes to
violate causality would result in their decay. In string theory Eric Gimon and Petr Hořava have argued that in a supersymmetric
five-dimensional Gödel universe quantum corrections to general
relativity effectively cut off regions of spacetimes with
causality-violating closed timelike curves.
In particular, in the
quantum theory a smeared supertube is present that cuts the
spacetime in such a way that, although in the full spacetime a
closed timelike curve passed through every point, no complete curves
exist on the interior region bounded by the tube.
FTL phenomena
In these examples, certain
influences may appear to travel faster than light, but they do not
convey energy or information faster than light, so they do not
violate special relativity.
Daily motion of the Heavens
For an earthbound observer objects in
the sky complete one revolution around the earth in 1 day.
Alpha
Centauri which is the nearest star outside the Solar system is about
4 light years away. On a geostationary view Alpha Centauri has a
speed many times greater than "c" as the rim speed of an object
moving in a circle is a product of the radius and angular speed. It
is also possible on a geostatic view for objects such as comets to
vary their speed from subluminal to superluminal and vice versa
simply because the distance from the earth varies. Comets may have
orbits which take them out to more than 1000 AU.
Circumference of a
circle radius 1000 AU is greater than one light day. In other words,
a comet at such a distance is superluminal in a geostatic frame.
Light spots and shadows
If a laser is swept across a distant object, the spot of light can
easily be made to move at a speed greater than c. Similarly, a
shadow projected onto a distant object can be made to move faster
than c. In neither case does any matter or information travel faster
than light.
Closing speeds
An observer may conclude that two objects are moving faster than
the speed of light relative to each other, by adding their
velocities according to the principle of Galilean relativity.
For example, two fast-moving particles approaching each other from
opposite sides of a particle accelerator will appear to be moving at
slightly less than twice the speed of light, relative to each other,
from the point of view of an observer standing at rest relative to
the accelerator.
This correctly reflects the rate at which the
distance between the two particles is decreasing, from the
observer's point of view and is called the closing speed. However,
it is not the same as the velocity of one of the particles as would
be measured by a hypothetical fast-moving observer traveling
alongside the other particle. To obtain this, the calculation must
be done according to the principle of special relativity.
If the two
particles are moving at velocities v and -v, or expressed in units
of c, β and − β, where
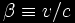
then this relative velocity (again in
units of the speed of light c) is
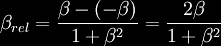
which is less than the speed of light.
Proper speeds
If a spaceship travels to a planet one light year (as measured in
the Earth's rest frame) away from Earth at high speed, the time
taken to reach that planet could be less than one year as measured
by the traveler's clock (although it will always be more than one
year as measured by a clock on Earth).
The value obtained by
dividing the distance traveled, as determined in the Earth's frame,
by the time taken, measured by the traveler's clock, is known as a
proper speed or a proper velocity. There is no limit on the value of
a proper speed as a proper speed does not represent a speed measured
in a single inertial frame.
A light signal that left the Earth at
the same time as the traveler would always get to the destination
before the traveler.
Phase velocities above c
The phase velocity of an electromagnetic
wave, when traveling through a medium, can routinely exceed c, the
vacuum velocity of light.
For example, this occurs in most glasses
at X-ray frequencies. However, the phase velocity of a wave
corresponds to the propagation speed of a theoretical
single-frequency (purely monochromatic) component of the wave at
that frequency. Such a wave component must be infinite in extent and
of constant amplitude (otherwise it is not truly monochromatic), and
so cannot convey any information.
Thus a phase velocity above c does
not imply the propagation of signals with a velocity above c.
Group velocities above c
The group velocity of a wave (e.g. a light beam) may also exceed c
in some circumstances. In such cases, which typically at the same
time involve rapid attenuation of the intensity, the maximum of the
envelope of a pulse may travel with a velocity above c.
However,
even this situation does not imply the propagation of signals with a
velocity above c, even though one may be tempted to associate pulse
maxima with signals. The latter association has been shown to be
misleading, basically because the information on the arrival of a
pulse can be obtained before the pulse maximum arrives.
For example,
if some mechanism allows the full transmission of the leading part
of a pulse while strongly attenuating the pulse maximum and
everything behind, the pulse maximum is effectively shifted forward
in time, while the information on the pulse does not come faster
than without this effect.
Universal expansion
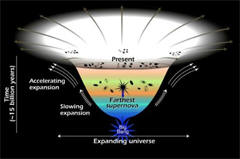
The expansion of the universe causes
distant galaxies to recede from us faster than the speed of light,
if commoving distance and cosmological time are used to calculate the
speeds of these galaxies.
However, in general relativity, velocity
is a local notion, so velocity calculated using commoving coordinates
does not have any simple relation to velocity calculated locally.
Rules that apply to relative velocities in special relativity, such
as the rule that relative velocities cannot increase past the speed
of light, do not apply to relative velocities in commoving
coordinates, which are often described in terms of the "expansion of
space" between galaxies.
This expansion rate is thought to have been
at its peak during the inflationary epoch thought to have occurred
in a tiny fraction of the second after the Big Bang (models suggest
the period would have been from around 10-36 seconds after the Big
Bang to around 10-33 seconds), when the universe may have rapidly
expanded by a factor of around 1020 – 1030.
Astronomical observations
Apparent superluminal motion is observed in many radio galaxies,
blazars, quasars and recently also in microquasars.
The effect was
predicted before it was observed by Martin Rees and can be explained
as an optical illusion caused by the object partly moving in the
direction of the observer, when the speed calculations assume it
does not.
The phenomenon does not contradict the theory of special
relativity. Interestingly, corrected calculations show these objects
have velocities close to the speed of light (relative to our
reference frame). They are the first examples of large amounts of
mass moving at close to the speed of light.
Earth-bound laboratories
have only been able to accelerate small numbers of elementary
particles to such speeds.
Quantum mechanics

Certain phenomena in quantum mechanics,
such as quantum entanglement, appear to transmit information faster
than light.
According to the No-communication theorem these
phenomena do not allow true communication; they only let two
observers in different locations see the same event simultaneously,
without any way of controlling what either sees. Wavefunction
collapse can be viewed as an epiphenomenon of quantum decoherence,
which in turn is nothing more than an effect of the underlying local
time evolution of the wavefunction of a system and all of its
environment.
Since the underlying behavior doesn't violate local
causality or allow FTL it follows that neither does the additional
effect of wavefunction collapse, whether real or apparent.
The uncertainty principle implies that individual photons may travel
for short distances at speeds somewhat faster (or slower) than c,
even in a vacuum; this possibility must be taken into account when
enumerating Feynman diagrams for a particle interaction.
To quote Richard Feynman:
…there is also an amplitude for
light to go faster (or slower) than the conventional speed of
light. You found out in the last lecture that light doesn't go
only in straight lines; now, you find out that it doesn't go
only at the speed of light! It may surprise you that there is an
amplitude for a photon to go at speeds faster or slower than the
conventional speed, c.
– Richard Feynman
However, macroscopically these
fluctuations average out, so that photons do travel in straight
lines over long (i.e. non-quantum) distances, and they do travel at
the speed of light on average.
Therefore, this does not imply the
possibility of superluminal information transmission.
There have been various reports in the popular press of experiments
on faster-than-light transmission in optics - most often in the
context of a kind of quantum tunneling phenomenon. Usually, such
reports deal with a phase velocity or group velocity faster than the
vacuum velocity of light. But, recall from above, that a
superluminal phase velocity cannot be used for faster-than-light
transmission of information.
There has sometimes been confusion
concerning the latter point.

Quantum teleportation transmits quantum
information at whatever speed is used to transmit the same amount of
classical information, likely the speed of light.
This quantum
information may theoretically be used in ways that classical
information can not, such as in quantum computations involving
quantum information only available to the recipient.
In science
fiction, quantum teleportation is either used as a basis for
teleportation of physical objects at the speed of light, presumably
preserving some important aspect of the entanglement between the
particles of the object, or else is misrepresented as allowing
faster-than-light communication.
Say you have 4 pairs of entangled
matter such that (x0,y0) are distinct from and won't affect
(x1,y1), (x2,y2), etc. If y0 changes you know that x0 changed,
the same being true for the other pairs. Right there you have a
nibble's worth of information transfer any time x0, x1, x2, etc.
are changed immediately altering y0, y1, and y2 respectively.
Monitoring the y bits will immediately tell you when the
entangled x bits are updated.
– SkewsMe.com
Hartman effect

The Hartman
Effect
The Hartman effect is the tunneling effect through a barrier where
the tunneling time tends to a constant for large barriers.
This was
first described by Thomas Hartman in 1962. This could, for instance,
be the gap between two prisms. When the prisms are in contact, the
light passes straight through, but when there is a gap, the light is
refracted. There is a finite probability that the photon will tunnel
across the gap rather than follow the refracted path. For large gaps
between the prisms the tunneling time approaches a constant and thus
the photons appear to have crossed with a superluminal speed.
However, an analysis by Herbert Winful from the University of
Michigan suggests that the Hartman effect cannot actually be used to
violate relativity by transmitting signals faster than c, because
the tunneling time,
"should not be linked to a velocity since
evanescent waves do not propagate".
Winful means by this that the
photons crossing the barrier are virtual photons only existing in
the interaction and could not be propagated into the outside world.
Casimir effect
In physics, the Casimir effect or Casimir-Polder force is a physical
force exerted between separate objects due to resonance of vacuum
energy in the intervening space between the objects.
This is
sometimes described in terms of virtual particles interacting with
the objects, due to the mathematical form of one possible way of
calculating the strength of the effect. Because the strength of the
force falls off rapidly with distance, it is only measurable when
the distance between the objects is extremely small. Energy appears
suddenly as if it came from the vacuum.
See Option B above for a
discussion of whether or not this effect could actually be used to
send signals faster than c or violate causality.
EPR Paradox

We can also quote the spectacular case
of the thought experiment of Einstein, Podolski and Rosen (EPR
paradox) which could be realized in experiments for the first time
by Alain Aspect in 1981 and 1982 in the Aspect experiment.
In this
case, the measurement of the state on one of the quantum systems of
an entangled pair forces the other system to be measured in the
complementary state. Thus functions quantum teleportation.
An experiment performed in 1997 by Nicolas Gisin at the University
of Geneva has demonstrated nonlocal quantum correlations between
particles separated by over 10 kilometers. But as noted earlier, the
nonlocal correlations seen in entanglement cannot actually be used
to transmit classical information faster than light, so that
relativistic causality is preserved; see no-communication theorem
for further information.
A 2008 quantum physics experiment also
performed by Nicolas Gisin and his colleagues in Geneva, Switzerland
has determined that the "speed" of the quantum non-local connection
(what Einstein called spooky action at a distance) has a minimum
lower bound of 10,000 times the speed of light.
Delayed choice quantum eraser

Delayed Choice
Quantum Eraser
Delayed choice quantum eraser (an experiment of Marlan Scully) is a
version of the EPR paradox in which the observation or not of
interference after the passage of a photon through a double slit
experiment depends on the conditions of observation of a second
photon entangled with the first.
The characteristic of this
experiment is that the observation of the second photon can take
place at a later time than the observation of the first photon,
which may give the impression that the measurement of the later
photons "retroactively" determines whether the earlier photons show
interference or not, although the interference pattern can only be
seen by correlating the measurements of both members of every pair
and so it can't be observed until both photons have been measured,
ensuring that an experimenter watching only the photons going
through the slit does not obtain information about the other photons
in an FTL or backwards-in-time manner.
Variable speed of light
In conventional physics, the speed of light in a vacuum is assumed
to be a constant. There exist theories which postulate that the
speed of light is not a constant.
The interpretation of this
statement is as follows.
Variable Speed of
Light
The speed of light is a dimensional
quantity and so, as has been emphasized in this context by João
Magueijo, it cannot be measured.
Measurable quantities in physics
are, without exception, dimensionless, although they are often
constructed as ratios of dimensional quantities. For example, when
you measure the height of a mountain you really measure the ratio of
its height to the length of a meterstick. The conventional SI system
of units is based on seven basic dimensional quantities, namely
distance, mass, time, electric current, thermodynamic temperature,
amount of substance, and luminous intensity.
These units are defined
to be independent and so cannot be described in terms of each other.
As an alternative to using a particular system of units, one can
reduce all measurements to dimensionless quantities expressed in
terms of ratios between the quantities being measured and various
fundamental constants such as Newton's constant, the speed of light
and Planck's constant; physicists can define at least 26
dimensionless constants which can be expressed in terms of these
sorts of ratios and which are currently thought to be independent of
one another.
By manipulating the basic dimensional constants one can
also construct the Planck time, Planck length and Planck energy
which make a good system of units for expressing dimensional
measurements, known as Planck units.
Magueijo's proposal used a different set of units, a choice which he
justifies with the claim that some equations will be simpler in
these new units.
In the new units he fixes the fine structure
constant, a quantity which some people, using units in which the
speed of light is fixed, have claimed is time dependent. Thus in the
system of units in which the fine structure constant is fixed, the
observational claim is that the speed of light is time-dependent.
While it may be mathematically possible to construct such a system,
it is not clear what additional explanatory power or physical
insight such a system would provide, assuming that it does indeed
accord with existing empirical data.
Back to Contents
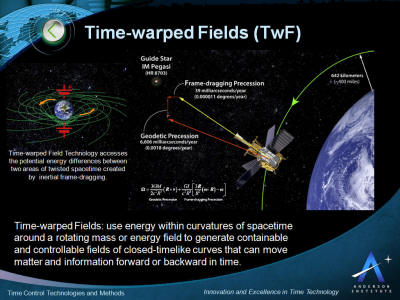
Time-warped Fields
Time-warped Fields use energy within curvatures of spacetime
surrounding a rotating mass or energy field to generate containable
and controllable fields of closed-timelike curves that can move
matter and information forward or backward in time.

David
Lewis Anderson, USAF
Officer and Scientist, founder of time-warped field theory.
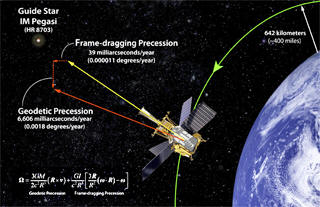
As general relativity predicts, rotating bodies drag spacetime
around themselves in a phenomenon referred to as frame-dragging.
This rotational frame-dragging effect is also known as the Lense-Thirring effect. The rotation of an object alters space and
time, dragging a nearby object out of position compared to the
predictions of Newtonian physics. The predicted effect is
small - about one part in a few trillion.
However, as Dr. David Lewis Anderson proposed in 1987 with his
announcement of time-warped field theory, the difference in
potential energy between two different areas of twisted spacetime
due to frame-dragging is significantly large. Even the smallest
twist in spacetime contains enormous energy potential and can be
used to create containable and controllable fields of close-timelike
curves without the need for significant input power. This makes both
forward and reverse time control possible within the limits of
technology today.
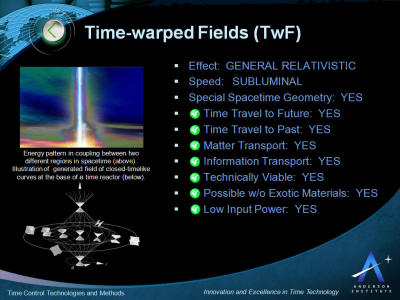
The key characteristics of the application of time-warped fields for
time control and time travel are presented in the picture below.
This is followed by more detail describing the science below.
Frame Dragging Effect Basics
The Anderson Time
Reactor operates by accessing the high energy
potential and effects, existing across two regions of twisted
spacetime,
to create containable and controllable fields of closed-timelike
curves.
Rotational frame-dragging appears in the general principle of
relativity and similar theories in the vicinity of rotating massive
objects.
Under this effect, the frame of reference in which a clock
ticks the fastest is one which is rotating around the object as
viewed by a distant observer. This also means that light traveling
in the direction of rotation of the object will move around the
object faster than light moving against the rotation as seen by a
distant observer. It is now the best-known effect, partly thanks to
the Gravity Probe B experiment.
Linear frame dragging is the similarly inevitable result of the
general principle of relativity, applied to linear momentum.
Although it arguably has equal theoretical legitimacy to the
"rotational" effect, the difficulty of obtaining an experimental
verification of the effect means that it receives much less
discussion and is often omitted from articles on frame-dragging
Static mass increase is another effect.
The effect is an increase in
inertia of a body when other masses are placed nearby. While not
strictly a frame dragging effect, it is also derived from the same
equation of general relativity. It is a tiny effect that is
difficult to confirm experimentally.
Mathematical Derivation of Frame
Dragging
Frame-dragging may be illustrated most readily using the Kerr
metric, which describes the geometry of spacetime in the vicinity of
a mass M rotating with angular momentum J
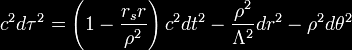
where rs is the Schwarzschild radius
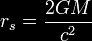
and where the following shorthand
variables have been introduced for brevity
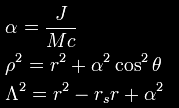
In the non-relativistic limit where M
(or, equivalently, rs) goes to zero, the Kerr metric becomes the
orthogonal metric for the oblate spheroidal coordinates
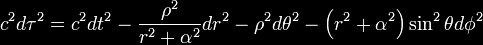
We may re-write the Kerr metric in the
following form
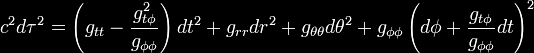
This metric is equivalent to a
co-rotating reference frame that is rotating with angular speed Ω
that depends on both the radius r and the colatitude θ
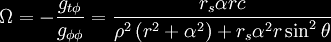
In the plane of the equator this
simplifies to:
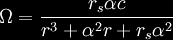
Thus, an inertial reference frame is
entrained by the rotating central mass to participate in the
latter's rotation; this is frame-dragging. Frame-dragging occurs
about every rotating mass and at every radius r and colatitude θ.
The Anderson Time Reactor
Twisted spacetime
around the earth, or
any rotating body, contains enormous
levels of potential energy. This is due
to the tension in the fabric of spacetime
caused by inertial frame-dragging.
Time-warped field theory shows how a properly configured energy beam
can be used to initiate and maintain the coupling of two different
areas of slightly twisted spacetime. This enables the discharge of
significantly greater levels of stored potential energy and
generates controllable fields of closed-timelike curves. The system
that couples these two regions of different spacetime potential is
common referred to as an Anderson Time Reactor or spacetime battery.
The Anderson Time Reactor is a system that couples two different
areas of twisted spacetime, with two different spacetime tensions.
The system can access and create a conduit to harvest that stored
energy and through the coupling process create dense fields of
Closed Timelike Curves (CTCs).
A reactor consists of a region of spacetime, large or small,
surrounding a rotating mass, where inertial frame dragging effects
are present twisting spacetime between two regions of space.

David Lewis
Anderson
A specialized beam emitter, with a localized source nearer to the
rotating mass, is directed toward a more distant region of space,
across the region of twisted spacetime created by inertial
frame-dragging.
A series of power collectors near and surrounding the beam emitter
provide a conduit to then channel and control the received power.
The resulting effect is that the potential energy in the twisted
fabric of spacetime is coupled or bridged from the distant point to
the local power collector array. The entire process is initiated and
controlled by the system.
The Anderson Time Reactor system achieves this by using the
application of Time-warped Field theory to create the ability to
leak, tap into and control the greater energy stored in this
spacetime tension (or energy potential difference), in between the
distant point and the localized point in spacetime.
In the most basic terms, the Time Reactor can be looked at as a
simple spacetime battery, accessing the significant potential energy
that existing around any rotating body anywhere in spacetime.
Spacetime-Motive Force

Spectral image of
energy pattern
near time reactor emitter and power
collector array showing coupling
and discharge of spacetime-motive
force including energy drift in the
direction of inertial frame dragging
of the Earth. New Mexico, USA, 2008
The coupling of these two points accesses what Dr. Anderson labeled
a "spacetime-motive force" with the ability to produce high energy
and time-warped fields allowing the containment and controlling of
fields of closed-timelike curves.
The force between the localized and distant point is called the open
spacetime-motive force. The open spacetime-motive force, even in the
minimal effects of inertial frame-dragging, can be extremely large
by present-day power generation standard standards. It is estimated
that a single next-generation time reactor may have the ability to
produce more than all of the worlds combined power generation
capabilities today.
The amount of spacetime motive force depends on several factors.
These include the mass of the rotating body, its rotation speed,
relative orientation of the two point to the axis of rotation, and
the medium and distance between the localized and distant points in
space. More simply, it is a function of the degree of inertial
frame-dragging and the characteristics of the medium through which
the Time Reactor must operate between the two regions to open a
"discharge path."
Also, the amount of energy that is accessed, or
time-warped fields generated, can be controlled in several ways
through phasing and other characteristics of the emitter and power
collector array.
A Practical Approach to Achieving Time
Control
Practical time control and time travel requires significantly large
energy levels, from some source, to operate effectively.
To achieve
time control we can attempt to generate this large energy level or,
as an alternative, access and channel the energy already existing
and inherent in natural processes and the basic makeup or fabric of spacetime surrounding our planet.
As stated above, it is estimated that a single next-generation time
reactor may have the ability to produce more than all of the world's
combined power generation capabilities today.
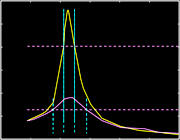
Time-warped field
theory demonstrates
a practical way to generate the
necessary concentrated CTCs and
high power levels, without high input
power, for practical time control
The fabric of spacetime is elastic and very powerful. It takes a
tremendous amount of power to create even the slightest twist in
spacetime. One can think of the fabric of spacetime surrounding a
rotating mass, like the Earth, to be a spring or a battery.
The rotating mass creates a twist in the fabric of spacetime who's
natural state and desire is to unwind, just like a spring, or to
discharge, just like a battery. Time-warped field technology uses
relatively low input power to open a discharge path for this
spacetime battery.
This technology itself does not create the energy
levels required for time control and time travel. Instead, it relies
on and operates using the energy stored within twisted spacetime
around a rotating body that is created by the inertial
frame-dragging effect. With only a small amount of system input
power, time-warped field theory shows how enormous power levels can
be accessed.
The coupling and discharge process, initiated and also defined by
time-warped field theory and technology, generates significant
levels of spacetime-motive force that can be used to generate very
concentrated fields of closed-timelike curves near the Time
Reactor's emitter and power collector array.
These fields of closed-timelike
curves are concentrated and controllable and can permit both forward
and backwards time control.
Back to Contents
Circulating Light Beams
Circulating Light Beams can be created using gamma and magnetic
fields to warp time. The approach can twist space that causes time
to be twisted, meaning you could theoretically walk through time as
you walk through space.

A number of interesting post-Newtonian
phenomena are known to occur for rotating distributions of matter in
Einstein’s general theory of relativity.
Inertial frame dragging,
for example, is a consequence of the weak gravitational field of a
slowly rotating massive sphere. In addition, exact solutions of the
Einstein field equations indicate the presence of closed timelike
lines for rotating Kerr black holes, van Stockum rotating dust
cylinders, and the rotating universe of Gödel.
The key characteristics of the application of circulating light
beams for time control and time travel are presented in the picture
below.
This is followed by more detail describing the approach
below.

Recently, Ronald L. Mallett solved the
linearized Einstein field equations to obtain the gravitational
field produced by the electromagnetic radiation of a unidirectional
ring laser.
It was shown that a massive spinning neutral particle at
the center of the ring laser exhibited inertial frame dragging.

Ronald L Mallett
Traveling close to the speed of light will slow a clock, even an
atomic clock. Likewise, a clock outside our atmosphere, far away
from any gravitational pull, will run faster than a clock on earth.
Therefore, if an artificial gravitational force were created, time
travel would, in theory, be possible.
Mallett believes he has found a way to make it happen. By trapping
light inside a photonic crystal, he can cause it to circulate. The
energy of the circulating light will cause the space inside the
circle to twist, causing a gravitational force.
This concept can be thought of as a spoon stirring a pot. The light
is the spoon rotating around the inner rim of the pot. The space is
the liquid being swirled by the spoon. As the space twists, it will
coil the normally linear passage of time with it, spiraling the
past, present, and future together into one continuous loop. It is
this twisting of space and time that Mallett believes will make time
travel possible.
Mallett and his partner at the University of Connecticut, Dr.
Chandra Raychoudhuri, are seeking National Science Foundation
funding for experiments that they hope will support their theories.
Their first experiment will be to trap light in a crystal and
observe the reaction of a neutron inside the circle.
Mallett will insert polarized neutrons
(neutrons that all spin in one direction) into the center of the
circulating light.
If he sees a change in their spin he will know
that space is indeed being twisted inside of the crystal. Should
this experiment prove successful, the team will apply for funding to
conduct studies to see if time bending is evident inside the circle
of light.
Dr. Mark Silverman at Trinity College in nearby Hartford has
suggested a possible way to see evidence of time bending: Two
identical samples of a radioactive substance would be prepared with
identical half-lives. One would be introduced into the time machine
circulating in the same direction as the light, the other in the
opposite direction.
If, at the end of the experiment, one sample had
decayed further than the other, Mallett's theories of time travel
would be supported.

Where the experiments will go from there
is unclear.
There is a vast difference between slowing the decay
rate of a radioactive particle and sending a human back in time.
Science aside, sending people through time creates philosophical
issues as well as physical ones. Consider the "Grandparent Paradox"
in which a time traveler goes back in time and kills her
grandparents, thus negating her entire existence. If she were never
born, then she couldn't go back in time in the first place.
Mallett
explains paradoxes such as these with a parallel-universe theory. He
believes that with every decision we make, another version of us
makes the opposite decision and splits off into a parallel universe.
Thus the time traveler was born in the universe where she did not
kill her grandparents.
This is where the line between philosophy and physics seems to blur.
"All of these things have their root in philosophy," says Mallett.
But he explains that the difference between physics and philosophy
is experiment.
"All of these things would be philosophy without
experimentation," he says.
True, the parallel-universe theory has
not been directly supported by experiment, but Mallett uses the
Heisenberg Uncertainty Principle to explain
why the parallel universe theory is probable.
Heisenberg's Uncertainty Principle says that we cannot predict both
the position of an electron and its spin at any given moment.
Without this principle,
"the universe should have collapsed
immediately after it was formed," says Mallett.
A hydrogen atom, one
of the building blocks of our universe, consists of a proton and an
electron. Since the proton and electron have opposite charges they
should be attracted to each other, collide, and destroy the atom.
But if that happened, we would know both the position of the
electron (the point of impact with the proton) and its spin (none);
therefore it is impossible for them to collide.

Sun distorting
spacetime.
Similar to the Uncertainty Principle, quantum mechanics works on the
theory that one can't make a definite prediction about anything that
will happen next.
Therefore the parallel-universe theory works well.
What will happen next can't be predicted because in fact, everything
happens next.
It has long been known(3, 4) that the van Stockum solution for the
exterior metric of an infinitely long rotating dust cylinder
contains closed timelike lines. Dr. Mallett has proposed that closed
timelike curves also
occur for an infinitely long circulating cylinder of light. This
model also shares some of the same limitations as the van Stockum
solution in that the metric is not asymptotically flat, however, has
emphasized that certain aspects of an infinitely long rotating dust
cylinder may be shared by a long finite one.
This may also apply to
a long but finite circulating cylinder of light.
Back to Contents
Wormholes
Since the 1930’s, physicists have speculated about the existence of
"wormholes" in the fabric of space.
Wormholes are hypothetical areas
of warped spacetime with great energy that can create tunnels
through spacetime. if traversable would allow a traveler to quickly
move through great distances in space and also travel through time.
The difficulty lies in keeping the wormhole open while the traveler
makes his journey: If the opening snaps shut, he will never survive
to emerge at the other end.
For years, scientists believed that the transit was physically
impossible.
But recent research, especially by the U.S. physicist
Kip Thorne, suggests that it could be done using exotic materials
capable of withstanding the immense forces involved. Even then, the
time machine would be of limited use – for example, you could not
return to a time before the wormhole was created.
Using wormhole
technology would also require a society so technologically advanced
that it could master and exploit the energy within black holes.
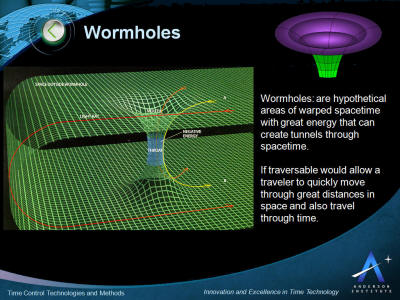

Hermann Weyl
Spacetime can be viewed as a 2D surface (to simplify understanding)
that, when 'folded' over, allows the formation of a wormhole bridge.
A wormhole has at least two mouths that are connected to a single
throat or tube. If the wormhole is traversable, then matter can
'travel' from one mouth to the other by passing through the throat.
While there is no observational evidence for wormholes, spacetime
containing wormholes are known to be valid solutions in general
relativity.

John Archibald
Wheeler
The term wormhole was coined by the American theoretical physicist
John Archibald Wheeler in 1957.
However, the idea of wormholes had
already been theorized in 1921 by the German mathematician Hermann Weyl in connection with his analysis of mass in terms of
electromagnetic field energy.
This analysis forces one to consider situations...where there is a
net flux of lines of force through what topologists would call a
handle of the multiply-connected space and what physicists might
perhaps be excused for more vividly terming a ‘wormhole’.
The key characteristics of the application of wormholes for time
control and time travel are presented in the picture below.
This is
followed by more detail describing the science below.

Definition
The basic notion of an intra-universe wormhole is that it is a
compact region of spacetime whose boundary is topologically trivial
but whose interior is not simply connected. Formalizing this idea
leads to definitions such as the following, taken from Matt Visser's
Lorentzian Wormholes.
If a Minkowski spacetime contains a compact region Ω, and if the
topology of Ω is of the form Ω ~ R x Σ, where Σ is a three-manifold
of nontrivial topology, whose boundary has topology of the form dΣ ~
S2, and if, furthermore, the hypersurfaces Σ are all spacelike, then
the region Ω contains a quasi-permanent intra-universe wormhole.
Characterizing inter-universe wormholes is more difficult. For
example, one can imagine a 'baby' universe connected to its 'parent'
by a narrow 'umbilicus'. One might like to regard the umbilicus as
the throat of a wormhole, but the spacetime is simply connected.
Schwarzschild wormholes
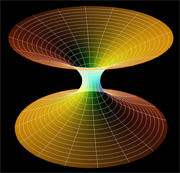
Diagram of a
Schwarzschild Wormhole
Lorentzian wormholes known as Schwarzschild wormholes or
Einstein-Rosen bridges are bridges between areas of space that can
be modeled as vacuum solutions to the Einstein field equations by
combining models of a black hole and a white hole.
This solution was
discovered by Albert Einstein and his colleague Nathan Rosen, who
first published the result in 1935. However, in 1962 John A. Wheeler
and Robert W. Fuller published a paper showing that this type of
wormhole is unstable, and that it will pinch off instantly as soon
as it forms, preventing even light from making it through.
Before the stability problems of Schwarzschild wormholes were
apparent, it was proposed that quasars were white holes forming the
ends of wormholes of this type.
While Schwarzschild wormholes are not traversable, their existence
inspired Kip Thorne to imagine traversable wormholes created by
holding the 'throat' of a Schwarzschild wormhole open with exotic
matter (material that has negative mass/energy).
Traversability
Wormholes would
act as shortcuts
connecting distant regions of space-time.
By going through a wormhole, it might
be possible to travel between the two
regions faster than a beam of light
through normal space-time.
Lorentzian traversable wormholes would allow travel from one part of
the universe to another part of that same universe very quickly or
would allow travel from one universe to another.
The possibility of
traversable wormholes in general relativity was first demonstrated
by Kip Thorne and his graduate student Mike Morris in a 1988 paper;
for this reason, the type of traversable wormhole they proposed,
held open by a spherical shell of exotic matter, is referred to as a
Morris-Thorne wormhole. Later, other types of traversable wormholes
were discovered as allowable solutions to the equations of general
relativity, including a variety analyzed in a 1989 paper by Matt Visser, in which a path through the wormhole can be made in which
the traversing path does not pass through a region of exotic matter.
However in the pure Gauss-Bonnet theory exotic matter is not needed
in order for wormholes to exist- they can exist even with no matter.
A type held open by negative mass cosmic strings was put forth by Visser in collaboration with Cramer et al., in which it was proposed
that such wormholes could have been naturally created in the early
universe.
Wormholes connect two points in spacetime, which means that they
would in principle allow travel in time, as well as in space. In
1988, Morris, Thorne and Yurtsever worked out explicitly how to
convert a wormhole traversing space into one traversing time.[4]
However, it has been said a time traversing wormhole cannot take you
back to before it was made but this is disputed.
Faster-than-light travel
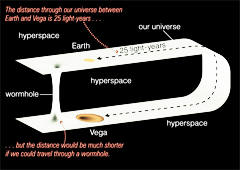
Special relativity only applies locally.
Wormholes allow superluminal (faster-than-light) travel by ensuring
that the speed of light is not exceeded locally at any time. While
traveling through a wormhole, subluminal (slower-than-light) speeds
are used. If two points are connected by a wormhole, the time taken
to traverse it would be less than the time it would take a light
beam to make the journey if it took a path through the space outside
the wormhole.
However, a light beam traveling through the wormhole
would always beat the traveler. As an analogy, running around to the
opposite side of a mountain at maximum speed may take longer than
walking through a tunnel crossing it.
You can walk slowly while
reaching your destination more quickly because the distance is
smaller.
Time travel
A wormhole could allow time travel.
This
could be accomplished by accelerating one end of the wormhole to a
high velocity relative to the other, and then sometime later
bringing it back; relativistic time dilation would result in the
accelerated wormhole mouth aging less than the stationary one as
seen by an external observer, similar to what is seen in the twin
paradox.
However, time connects differently through the wormhole
than outside it, so that synchronized clocks at each mouth will
remain synchronized to someone traveling through the wormhole
itself, no matter how the mouths move around. This means that
anything which entered the accelerated wormhole mouth would exit the
stationary one at a point in time prior to its entry.
For example, consider two clocks at both mouths both showing the
date as 2000.
After being taken on a trip at relativistic
velocities, the accelerated mouth is brought back to the same region
as the stationary mouth with the accelerated mouth's clock reading
2005 while the stationary mouth's clock read 2010. A traveler who
entered the accelerated mouth at this moment would exit the
stationary mouth when its clock also read 2005, in the same region
but now five years in the past.
Such a configuration of wormholes
would allow for a particle's world line to form a closed loop in spacetime, known as a closed timelike curve.
It is thought that it may not be
possible to convert a wormhole into a time machine in this manner;
some analyses using the semi-classical approach to incorporating
quantum effects into general relativity indicate that a feedback
loop of virtual particles would circulate through the wormhole with
ever-increasing intensity, destroying it before any information
could be passed through it, in keeping with the chronology
protection conjecture.
This has been called into question by the
suggestion that radiation would disperse after traveling through the
wormhole, therefore preventing infinite accumulation. The debate on
this matter is described by Kip S. Thorne in the book Black Holes
and Time Warps. There is also the Roman ring, which is a
configuration of more than one wormhole.
This ring seems to allow a
closed time loop with stable wormholes when analyzed using
semi-classical gravity, although without a full theory of quantum
gravity it is uncertain whether the semi-classical approach is
reliable in this case.
Metrics
Theories of wormhole metrics describe the spacetime geometry of a
wormhole and serve as theoretical models for time travel. An example
of a (traversable) wormhole metric is the following:
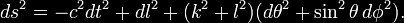
One type of non-traversable wormhole
metric is the Schwarzschild solution:
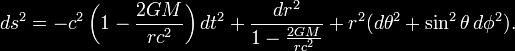
In fiction

Wing Commander ships
are configured
with jump drives to propel a spacecraft
between two connecting stellar systems.
Wormholes are features of science fiction as they allow interstellar
(and sometimes inter-universal) travel within human timescales.
It
is common for the creators of a fictional universe to decide that
faster-than-light travel is either impossible or that the technology
does not yet exist, but to use wormholes as a means of allowing
humans to travel long distances in short periods. Military science
fiction (such as the Wing Commander games) often uses a "jump drive"
to propel a spacecraft between two fixed "jump points" connecting
stellar systems.
Connecting systems in a network like this results
in a fixed "terrain" with choke points that can be useful for
constructing plots related to military campaigns. The Alderson
points used by Larry Niven and Jerry Pournelle in The Mote in God's
Eye and related novels are an example, although the mechanism does
not seem to describe actual wormhole physics.
David Weber has also
used the device in the Honorverse and other books such as those
based upon the Starfire universe. Naturally occurring wormholes form
the basis for interstellar travel in Lois McMaster Bujold's
Vorkosigan Saga. They are also used to create an Interstellar
Commonwealth in Peter F. Hamilton's Commonwealth Saga.
In Jack L. Chalker's The Rings of the Master series, interstellar class
spaceships are capable of calculating complex equations and punching
Wormholes in the fabric of the Universe in order to enable rapid
travel.
Concept of wormholes is used in The Wild Blue Yonder, a science
fiction film by Werner Herzog.
Mass Relay Map in
the Video Game Mars Effect
The Mass Relays in the videogame Mass Effect can be perceived as
stabilized wormholes that allow for near instantaneous,
"faster-than-light" travel from one end to the other.
The Massively Multiplayer Online Game EVE Online utilizes wormholes
extensively as they are created in the use of the stargate
technology which allows for interstellar travel in the game world.
The Vega Strike first-person space trading and combat simulator
features wormholes to travel through star systems. The engine is
open-source and has various mods and total conversions which have
wormholes too, like Vega Trek, a Vega Strike mod based on the Star
Trek universe.
Or the Privateer Remake, a remake of Wing Commander:
Privateer.

Bajoran Wormhole
in Star Trek
Wormholes also play pivotal roles in science fiction where
faster-than-light travel is possible though limited, allowing
connections between regions that would be otherwise unreachable
within conventional timelines.
Several examples appear in the Star
Trek franchise, including the Bajoran wormhole in the Deep Space
Nine series. In 1979's Star Trek: The Motion Picture the USS
Enterprise was trapped in an artificial wormhole caused by an
imbalance in the calibration of the ship's warp engines when it
first achieved faster-than-light speed.
In the Star Trek: Voyager
series, the cybernetic species the Borg use what, in the Star Trek
universe, are referred to as transwarp conduits, allowing ships to
move nearly instantaneously to any part of the galaxy in which an
exit aperture exists. Although these conduits are never described as
"wormholes", they appear to share several traits in common with
them.
The 1979 Disney film The Black Hole's plot centers around a massive
black hole, although it makes virtually no use of then-current
worm-hole physics, with only one rather desultory mention of an
Einstein-Rosen bridge.
A trip through the black hole turns
theological, abandoning scientific rationale.

Wormhole
Transporter in the
movie Contact.
In Carl Sagan's novel Contact and subsequent 1997 film starring
Jodie Foster and Matthew McConaughey, Foster's character Ellie
travels 26 light years through a series of wormholes to the star
Vega.
The round trip, which to Ellie lasts 18 hours, passes by in a
fraction of a second on Earth, making it appear she went nowhere. In
her defense, Foster mentions an Einstein-Rosen bridge and tells how
she was able to travel faster than light and time. Analysis of the
situation by Kip Thorne, on the request of Sagan, is quoted by
Thorne as being his original impetus for analyzing the physics of
wormholes.
Wormholes play major roles in the television series Farscape, where
they are the cause of John Crichton's presence in the far reaches of
our own galaxy, and in the Stargate series, where stargates create a
stable artificial wormhole where matter is dematerialized, converted
into energy, and is sent through to be rematerialized at the other
side.
In the latter series, the devices were discovered in Egypt by
an archeologist, and were built by aliens known as the Ancients or
the Alterans. In the science fiction series Sliders, a wormhole (or
vortex, as it is usually called in the show) is used to travel
between parallel worlds, and one is seen at least once or twice in
every episode.
In the pilot episode it was referred to as an
"Einstein-Rosen-Podolsky bridge".
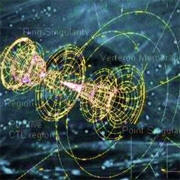
Wormhole in movie
Donnie Darko
The central theme in the movie Donnie Darko revolves around
Einstein-Rosen bridges.
It is possible that the Webway technology used by the Eldar of the
fictional Warhammer 40,000 could be perceived as wormhole
technology.
In Command & Conquer 3 and in its expansion the Scrin faction (an
alien life form with unknown origins from outer solar system) uses
artificial wormholes for military purposes to convey infantry and
vehicles behind enemy lines.
In the Invader Zim episode, "A Room with a Moose" Zim utilizes a
wormhole to send his classmates into a parallel universe that
consists entirely of a room with a large moose inside it.
The television series Strange Days at Blake Holsey High is about a
wormhole the science club found at their school.
In an episode called "wormhole" in the 13th season of the long
running American series Power Rangers, called Power Rangers SPD the
spd rangers go through a wormhole to team up with the previous team
of Power Rangers Dino Thunder from year 2004, after their enemy
Emperor Grumm goes through one.
In the video game "Supreme Commander" the UEF faction utilizes
aether-gates for long distance military strikes.

Black hole in
video game Spore
In the video game "Spore", the player can travel through various
black holes, which act as wormholes for the player to go to its
counterpart located usually on the other side of the galaxy;
something that would take much longer to do by flying there
manually.
In the 1995-1996 FOX military science fiction series SPACE: Above
and Beyond, during the first several episodes, the United Earth
Force travel through wormholes, called the "Kali Region" or "Galileo
Region" to arrive at exo-solar destinations. This idea is abandoned
after the second episode.
In the movie Race to Witch Mountain the 2 aliens from a planet which
is 3000 light years away from Earth use wormholes to travel to
Earth.
In the 2009 Doctor Who Easter special, Planet of the Dead, the
Doctor and a group of passengers aboard a double-decker bus are
transported to an alien world via a wormhole.
Back to Contents
Cosmic Strings
Cosmic Strings are a hypothetical 1-dimensional (spatially)
topological defect in the fabric of spacetime left over from the
formation of the universe. Interaction could create fields of closed
time-like curves permitting backwards time travel.
Some scientists have suggested using "cosmic strings" to construct a
time machine. By maneuvering two cosmic strings close together – or
possibly just one string plus a black hole – it is theoretically
possible to create a whole array of "closed time-like curves." Your
best bet is to fire two infinitely long cosmic strings past each
other at very high speeds, then fly your ship around them in a
carefully calculated figure eight. In theory, you would be able to
emerge anywhere, anytime!
At the moment, these are purely theoretical objects that might
possibly be left over from the creation of the universe in the Big
Bang. A black hole contains a one-dimensional singularity – an
infinitely small point in the space-time continuum. A cosmic string,
if such a thing existed, would be a two-dimensional infinitely thin
line that has even stranger effects on the fabric of space and time.
Although no one has actually found a cosmic string, astronomers have
suggested that they may explain strange effects seen in distant
galaxies.

A cosmic string is a 1-dimensional
(spatially) topological defect in various fields.
Cosmic strings are
hypothesized to form when the field undergoes a phase change in
different regions of spacetime, resulting in condensations of energy
density at the boundaries between regions. This is somewhat
analogous to the imperfections that form between crystal grains in
solidifying liquids, or the cracks that form when water freezes into
ice.
The phase changes that produce cosmic strings may have occurred
in the earliest moments of the universe's evolution.
The key characteristics of the application of cosmic strings for
time control and time travel are presented in the picture below.
This is followed by more detail describing the theory below.
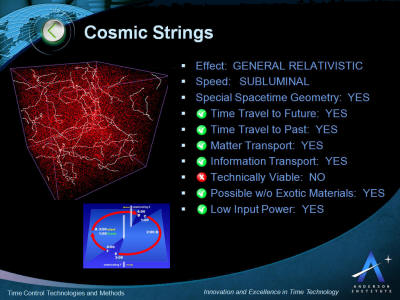
Cosmic strings, if they exist, would be
extremely thin with diameters on the same order as a proton.
They
would have immense density, however, and so would represent
significant gravitational sources. A cosmic string 1.6 kilometers in
length may be heavier than the Earth. However general relativity
predicts that the gravitational potential of a straight string
vanishes: there is no gravitational force on static surrounding
matter.
The only gravitational effect of a straight cosmic string is
a relative deflection of matter (or light) passing the string on
opposite sides (a purely topological effect). A closed loop of
cosmic string gravitates in a more conventional way. During the
expansion of the universe, cosmic strings would form a network of
loops, and their gravity could have been responsible for the
original clumping of matter into galactic superclusters.
A cosmic string's vibrations, which would oscillate near the speed
of light, can cause part of the string to pinch off into an isolated
loop. These loops have a finite lifespan due to decay via
gravitational radiation.
Other types of topological defects in spacetime are domain walls,
monopoles, and textures.
Observational evidence
It was once thought that the
gravitational influence of cosmic strings might contribute to the
large-scale clumping of matter in the universe, but all that is
known today through galaxy surveys and precision measurements of the
cosmic microwave background fits an evolution out of random,
Gaussian fluctuations.
These precise observations therefore tend to
rule out a significant role for cosmic strings.
Gravitational lensing of a galaxy by a straight section of a cosmic
string would produce two identical, undistorted images of the
galaxy.
In 2003 a group led by Mikhail Sazhin reported the
accidental discovery of two seemingly identical galaxies very close
together in the sky, leading to speculation that a cosmic string had
been found. However, observations by the Hubble Space Telescope in
January 2005 showed them to be a pair of similar galaxies, not two
images of the same galaxy.
A cosmic string would produce a similar
duplicate image of fluctuations in the cosmic microwave background,
which might be detectable by the upcoming Planck Surveyor mission.
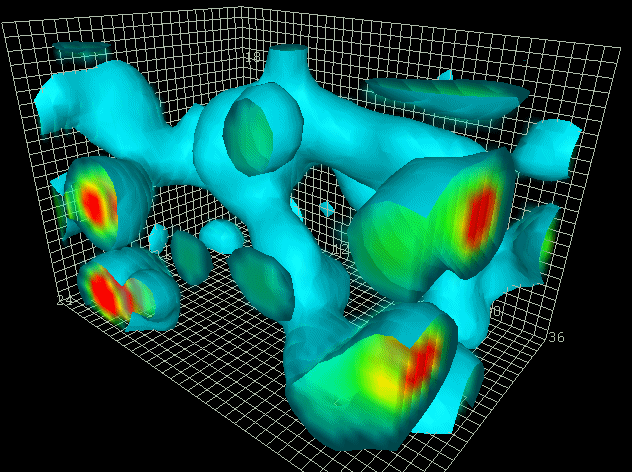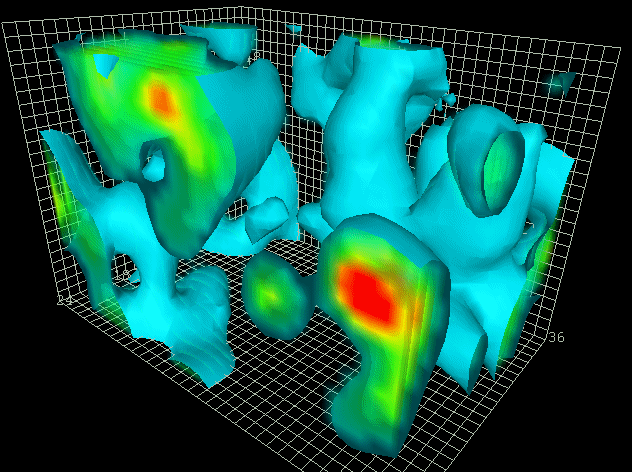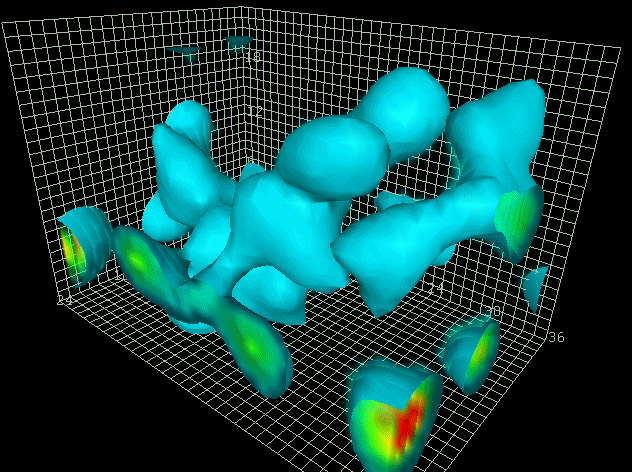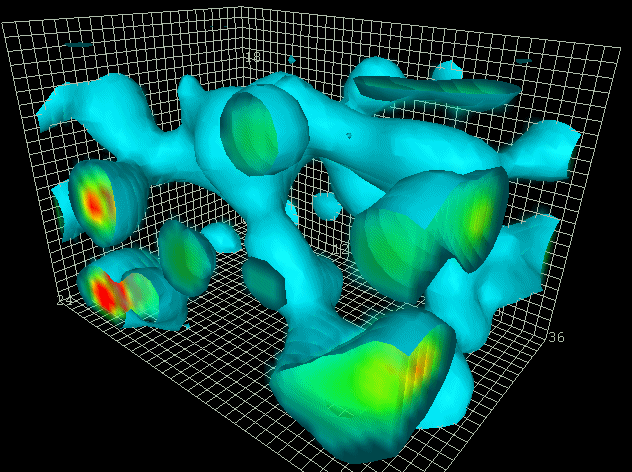
A second piece of evidence supporting
cosmic string theory is a phenomenon observed in observations of the
"double quasar" called Q0957+561A,B.
Originally discovered by Dennis
Walsh, Bob Carswell, and Ray Weymann in 1979, the double image of
this quasar is caused by a galaxy positioned between it and the
Earth. The gravitational lens effect of this intermediate galaxy
bends the quasar's light so that it follows two paths of different
lengths to Earth. The result is that we see two images of the same
quasar, one arriving a short time after the other (about 417.1 days
later).
However, a team of astronomers at the Harvard-Smithsonian Center for
Astrophysics led by Rudolph Schild studied the quasar and found that
during the period between September 1994 and July 1995 the two
images appeared to have no time delay; changes in the brightness of
the two images occurred simultaneously on four separate occasions.
Schild and his team believe that the only explanation for this
observation is that a cosmic string passed between the Earth and the
quasar during that time period traveling at very high speed and
oscillating with a period of about 100 days.
The Laser Interferometer Gravitational-Wave Observatory (LIGO) and
upcoming gravitational wave observatories will search for cosmic
strings as well as other phenomenon with the byproduct of
gravitational waves.
String theory and cosmic strings

There is no direct connection between
string theory and the theory of cosmic strings (the names were
chosen independently by analogy with ordinary string).
However, work
in string theory revived interest in cosmic strings in the early
2000s. In 2002 Henry Tye and collaborators observed the production
of cosmic strings during the last stages of brane inflation. It was
also pointed out by string theorist Joseph Polchinski that the
expanding Universe could have stretched a "fundamental" string (the
sort which superstring theory considers) until it was of
intergalactic size.
Such a stretched string would exhibit many of
the properties of the old "cosmic" string variety, making the older
calculations useful again. Furthermore, modern superstring theories
offer other objects which could feasibly resemble cosmic strings,
such as highly elongated one-dimensional D-branes (known as
"D-strings").
As theorist Tom Kibble remarks,
"string theory
cosmologists have discovered cosmic strings lurking everywhere in
the undergrowth".
Older proposals for detecting cosmic strings could
now be used to investigate superstring theory.

Scientists at the
LIGO Livingston Observatory in
Louisiana are searching for evidence of
gravitational waves.
Superstrings, D-strings or other stringy objects stretched to
intergalactic scales would radiate gravitational waves, which could
presumably be detected using experiments like LIGO. They might also
cause slight irregularities in the cosmic microwave background, too
subtle to have been detected yet but possibly within the realm of
future observability.
Note that most of these proposals depend, however, on the
appropriate cosmological fundamentals (strings, branes, etc.), and
no convincing experimental verification of these has been performed.
Back to Contents
Tipler Cylinder
A Tipler Cylinder uses a massive and long cylinder spinning around
its longitudinal axis. The rotation creates a frame-dragging effect
and fields of closed time-like curves traversable in a way to
achieve subluminal time travel to the past.
Civilizations with the technology to harness black holes might be
better advised to leave wormholes alone and try the time-warp method
suggested by U.S. astronomer Frank Tipler. He has a simple recipe
for a time machine: First take a piece of material 10 time the mass
of the Sun, squeeze it together and roll it into a long, thin,
super-dense cylinder – a bit like a black hole that has passed
through a spaghetti factory. Then spin the cylinder up to a few
billion revolutions per minute and see what happens.
Tipler predicts that a ship following a carefully plotted spiral
course around the cylinder would immediately find itself on a
"closed, time-like curve."
It would emerge thousands, even billions,
of years from its starting point and possibly several galaxies away.
There are problems, though. For the mathematics to work properly, Tipler’s cylinder has to be infinitely long. Also, odd things happen
near the ends and you need to steer well clear of them in your
timeship.
However, if you make the device as long as you can, and
stick to paths close to the middle of the cylinder, you should
survive the trip!
The Tipler cylinder, also called a
Tipler time machine, is a hypothetical object theorized to be a
potential mode of time travel - an approach that is conceivably
functional within humanity's current understanding of physics,
specifically the theory of general relativity, although later
results have shown that a Tipler cylinder could only allow time
travel if its length would appear infinite.
The key characteristics of the application of Tipler Cylinders for
time control and time travel are presented in the picture below.
This is followed by more detail describing the approach below.


Frank Tipler
The Tipler cylinder was discovered as a solution to the equations of
general relativity by Willem Jacob van Stockum in 1936 and Kornel
Lanczos in 1924, but not recognized as allowing closed timelike
curves until an analysis by Frank Tipler in 1974.
Tipler showed in
his 1974 paper, "Rotating Cylinders and the Possibility of Global
Causality Violation" that in a spacetime containing a massive,
infinitely long cylinder which was spinning along its longitudinal
axis, the cylinder should create a frame-dragging effect.
This
frame-dragging effect warps spacetime in such a way that the light
cones of objects in the cylinder's proximity become tilted, so that
part of the light cone then points backwards along the time axis on
a space time diagram.
Therefore a spacecraft accelerating
sufficiently in the appropriate direction can travel backwards
through time along a closed timelike curve or CTC.
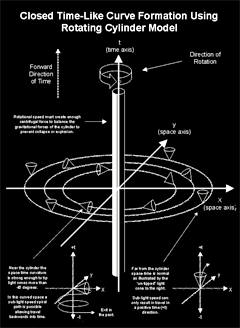
Closed timelike
curve formation
using rotating cylinder model
CTC's are associated, in Lorentzian manifolds which are interpreted
physically as spacetimes, with the possibility of causal anomalies
such as going back in time and potentially shooting your own
grandfather, although paradoxes might be avoided using some
constraint such as the Novikov self-consistency principle.
They have
an unnerving habit of appearing in some of the most important exact
solutions in general relativity, including the Kerr vacuum (which
models a rotating black hole) and the van Stockum dust (which models
a cylindrically symmetrical configuration of rotating pressureless
fluid or dust).
An objection to the practicality of building a Tipler cylinder was
discovered by Stephen Hawking, who posited a conjecture showing that
according to general relativity it is impossible to build a time
machine in any finite region that satisfies the weak energy
condition, meaning that the region contains no exotic matter with
negative energy.
The Tipler cylinder, on the other hand, does not involve any
negative energy.
Tipler's original solution involved a cylinder of
infinite length, which is easier to analyze mathematically, and
although Tipler suggested that a finite cylinder might produce
closed timelike curves if the rotation rate were fast enough, he did
not prove this.
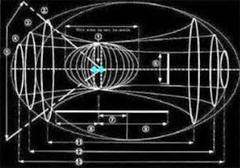
A spirallohedron of 6
hyperstrings
from 6 parallel universes
But Hawking argues that because of his conjecture,
"it can't be done
with positive energy density everywhere! I can prove that to build a
finite time machine, you need negative energy."
Hawking's proof
appears in his 1992 paper on the chronology protection conjecture,
where he examines,
"the case that the causality violations appear in
a finite region of spacetime without curvature singularities" and
proves that "there will be a Cauchy horizon that is compactly
generated and that in general contains one or more closed null
geodesics which will be incomplete. One can define geometrical
quantities that measure the Lorentz boost and area increase on going
round these closed null geodesics. If the causality violation
developed from a noncompact initial surface, the averaged weak
energy condition must be violated on the Cauchy horizon."
Back to Contents
Casimir Effect
The Casimer Effect is a physical force arising from a quantized
field, for example between two uncharged plates. This can produce a
locally mass-negative region of space-time that could stabilize a
wormhole to allow faster than light travel.
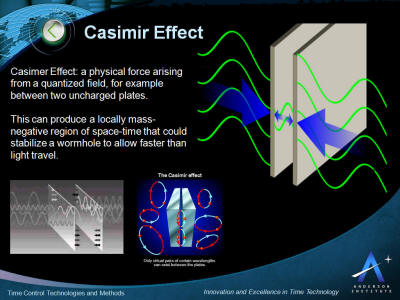
In quantum field theory, the Casimir
effect and the Casimir-Polder force are physical forces arising from
a quantized field.
The typical example is of two uncharged metallic
plates in a vacuum, placed a few micrometers apart, without any
external electromagnetic field. In a classical description, the lack
of an external field also means that there is no field between the
plates, and no force would be measured between them.
When this field
is instead studied using quantum electrodynamics, it is seen that
the plates do affect the virtual photons which constitute the field,
and generate a net force - either an attraction or a repulsion
depending on the specific arrangement of the two plates.
The key characteristics of the application of the Casimir Effect for
time control and time travel are presented in the picture below.
This is followed by more detail describing the effect below.
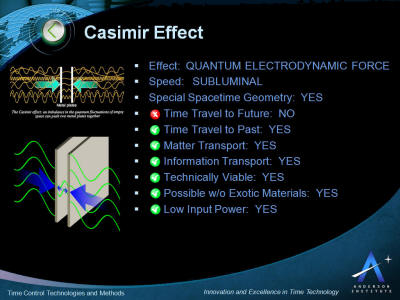
Although the Casimir effect can be
expressed in terms of virtual particles interacting with the
objects, it is best described and more easily calculated in terms of
the zero-point energy of a quantized field in the intervening space
between the objects.
This force has been measured, and is a striking
example of an effect purely due to second quantization. However, the
treatment of boundary conditions in these calculations has led to
some controversy. In fact "Casimir's original goal was to compute
the van der Waals force between polarizable molecules" of the
metallic plates.
Thus it can be interpreted without any reference to
the zero-point energy (vacuum energy) or virtual particles of
quantum fields.

Hendrik Casimir
Dutch physicists Hendrik B. G. Casimir and Dirk Polder proposed the
existence of the force and formulated an experiment to detect it in
1948 while participating in research at Philips Research Labs.
The
classic form of the experiment, described above, successfully
demonstrated the force to within 15% of the value predicted by the
theory.
Because the strength of the force falls
off rapidly with distance, it is only measurable when the distance
between the objects is extremely small.
On a submicrometre scale,
this force becomes so strong that it becomes the dominant force
between uncharged conductors. In fact, at separations of 10 nm - about
100 times the typical size of an atom - the Casimir effect produces
the equivalent of 1 atmosphere of pressure (101.3 kPa), the precise
value depending on surface geometry and other factors.
In modern theoretical physics, the Casimir effect plays an important
role in the chiral bag model of the nucleon; and in applied physics,
it is significant in some aspects of emerging microtechnologies and
nanotechnologies.
Vacuum energy
The causes of the Casimir effect are described by quantum field
theory, which states that all of the various fundamental fields,
such as the electromagnetic field, must be quantized at each and
every point in space.
In a simplified view, a "field" in physics may
be envisioned as if space were filled with interconnected vibrating
balls and springs, and the strength of the field can be visualized
as the displacement of a ball from its rest position.
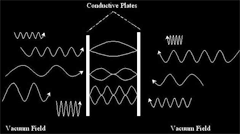
Vibrations in this field propagate and
are governed by the appropriate wave equation for the particular
field in question.
The second quantization of quantum field theory
requires that each such ball-spring combination be quantized, that
is, that the strength of the field be quantized at each point in
space. Canonically, the field at each point in space is a simple
harmonic oscillator, and its quantization places a quantum harmonic
oscillator at each point. Excitations of the field correspond to the
elementary particles of particle physics. However, even the vacuum
has a vastly complex structure, all calculations of quantum field
theory must be made in relation to this model of the vacuum.
The vacuum has, implicitly, all of the properties that a particle
may have: spin, or polarization in the case of light, energy, and so
on. On average, all of these properties cancel out: the vacuum is,
after all, "empty" in this sense. One important exception is the
vacuum energy or the vacuum expectation value of the energy.
The
quantization of a simple harmonic oscillator states that the lowest
possible energy or zero-point energy that such an oscillator may
have is
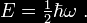
Summing over all possible oscillators at
all points in space gives an infinite quantity.
To remove this
infinity, one may argue that only differences in energy are
physically measurable; this argument is the underpinning of the
theory of renormalization. In all practical calculations, this is
how the infinity is always handled. In a deeper sense, however,
renormalization is unsatisfying, and the removal of this infinity
presents a challenge in the search for a Theory of Everything.
Currently there is no compelling explanation for how this infinity
should be treated as essentially zero; a non-zero value is
essentially the cosmological constant and any large value causes
trouble in cosmology.
The Casimir Effect
Simulation of
Casimir Force
Casimir's observation was that the second-quantized quantum
electromagnetic field, in the presence of bulk bodies such as metals
or dielectrics, must obey the same boundary conditions that the
classical electromagnetic field must obey. In particular, this
affects the calculation of the vacuum energy in the presence of a
conductor or dielectric.
Consider, for example, the calculation of the vacuum expectation
value of the electromagnetic field inside a metal cavity, such as,
for example, a radar cavity or a microwave waveguide.
In this case,
the correct way to find the zero point energy of the field is to sum
the energies of the standing waves of the cavity. To each and every
possible standing wave corresponds an energy; say the energy of the
nth standing wave is En. The vacuum expectation value of the energy
of the electromagnetic field in the cavity is then
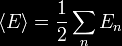
with the sum running over all possible
values of n enumerating the standing waves. The factor of 1/2
corresponds to the fact that the zero-point energies are being
summed - it is the same 1/2 as appears in the equation...
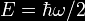
Written in
this way, this sum is clearly divergent; however, it can be used to
create finite expressions.
In particular, one may ask how the zero point energy depends on the
shape s of the cavity. Each energy level En depends on the shape,
and so one should write En(s) for the energy level, and,
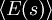
for the
vacuum expectation value. At this point comes an important
observation: the force at point p on the wall of the cavity is equal
to the change in the vacuum energy if the shape s of the wall is
perturbed a little bit, say by δs, at point p.
That is, one has
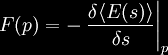
This value is finite in many practical
calculations.
Casimir's calculation
In the original calculation done by Casimir, he considered the space
between a pair of conducting metal plates at distance a apart.
In
this case, the standing waves are particularly easy to calculate,
since the transverse component of the electric field and the normal
component of the magnetic field must vanish on the surface of a
conductor. Assuming the parallel plates lie in the x-y plane, the
standing waves are
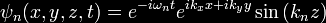
where ψ stands for the electric component of the electromagnetic
field, and, for brevity, the polarization and the magnetic
components are ignored here. Here,
kx and ky are the wave vectors in directions parallel to the plates,
and
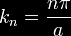
is the wave-vector perpendicular to the
plates. Here, n is an integer, resulting from the requirement that ψ
vanish on the metal plates. The energy of this wave is
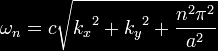
where c is the speed of light. The
vacuum energy is then the sum over all possible excitation modes
where A is the area of the metal plates,
and a factor of 2 is introduced for the two possible polarizations
of the wave. This expression is clearly infinite, and to proceed
with the calculation, it is convenient to introduce a regulator
(discussed in greater detail below). The regulator will serve to
make the expression finite, and in the end will be removed. The
zeta-regulated version of the energy per unit-area of the plate is
In the end, the limit
is to be taken. Here s is just a complex
number, not to be confused with the shape discussed previously. This
integral/sum is finite for s real and larger than 3. The sum has a
pole at s=3, but may be analytically continued to s=0, where the
expression is finite. Expanding this, one gets
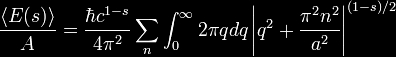
where polar coordinates
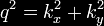
were introduced to turn the double
integral into a single integral. The q in front is the Jacobian, and
the 2π comes from the angular integration. The integral is easily
performed, resulting in
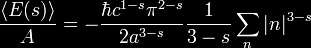
The sum may be understood to be the
Riemann zeta function, and so one has
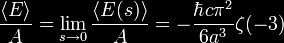
But ζ( − 3) = 1 / 120 and so one obtains
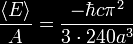
The Casimir force per unit area,
Fc / A for idealized, perfectly conducting plates with vacuum
between them is
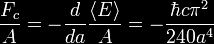
where
(hbar, ħ) is the reduced Planck
constant,
c is the speed of light,
a is the distance between the two plates.
The force is negative, indicating that
the force is attractive: by moving the two plates closer together,
the energy is lowered. The presence of shows that the Casimir force
per unit area Fc / A is very small, and that furthermore, the force
is inherently of quantum-mechanical origin.
More recent theory

Concept of
zero-point energy module
using the Casimir Effect
A very complete analysis of the Casimir effect at short distances is
based upon a detailed analysis of the van der Waals force by
Lifshitz. Using this approach, complications of the bounding
surfaces, such as the modifications to the Casimir force due to
finite conductivity, can be calculated numerically using the
tabulated complex dielectric functions of the bounding materials.
In
addition to these factors, complications arise due to surface
roughness of the boundary and to geometry effects such as degree of
parallelism of bounding plates. For boundaries at large separations,
retardation effects give rise to a long-range interaction. For the
case of two parallel plates composed of ideal metals in vacuum, the
results reduce to Casimir’s.
Measurement
One of the first experimental tests was conducted by Marcus Sparnaay
at Philips in Eindhoven, in 1958, in a delicate and difficult
experiment with parallel plates, obtaining results not in
contradiction with the Casimir theory, but with large experimental
errors.
The Casimir effect was measured more accurately in 1997 by Steve K.
Lamoreaux of Los Alamos National Laboratory and by Umar Mohideen and
Anushree Roy of the University of California at Riverside.
In
practice, rather than using two parallel plates, which would require
phenomenally accurate alignment to ensure they were parallel, the
experiments use one plate that is flat and another plate that is a
part of a sphere with a large radius. In 2001, a group at the
University of Padua finally succeeded in measuring the Casimir force
between parallel plates using microresonators.
Regularisation
In order to be able to perform calculations in the general case, it
is convenient to introduce a regulator in the summations. This is an
artificial device, used to make the sums finite so that they can be
more easily manipulated, followed by the taking of a limit so as to
remove the regulator.
The heat kernel or exponentially regulated sum is
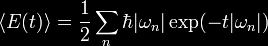
where the limit

is taken in the end. The divergence of
the sum is typically manifested as
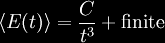
for three-dimensional cavities. The
infinite part of the sum is associated with the bulk constant C
which does not depend on the shape of the cavity. The interesting
part of the sum is the finite part, which is shape-dependent. The
Gaussian regulator
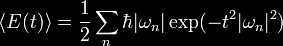
is better suited to numerical
calculations because of its superior convergence properties, but is
more difficult to use in theoretical calculations. Other, suitably
smooth, regulators may be used as well. The zeta function regulator
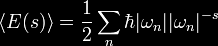
is completely unsuited for numerical
calculations, but is quite useful in theoretical calculations. In
particular, divergences show up as poles in the complex s plane,
with the bulk divergence at s=4.
This sum may be analytically
continued past this pole, to obtain a finite part at s=0.
Not every cavity configuration necessarily leads to a finite part
(the lack of a pole at s=0) or shape-independent infinite parts. In
this case, it should be understood that additional physics has to be
taken into account. In particular, at extremely large frequencies
(above the plasma frequency), metals become transparent to photons
(such as x-rays), and dielectrics show a frequency-dependent cutoff
as well.
This frequency dependence acts as a natural regulator.
There are a variety of bulk effects in solid state physics,
mathematically very similar to the Casimir effect, where the cutoff
frequency comes into explicit play to keep expressions finite.
(These are discussed in greater detail in Landau and Lifshitz,
"Theory of Continuous Media".)
Generalities

experimental
setup for the conversion of
vacuum energy into mechanical-energy.
The Casimir effect can also be computed using the mathematical
mechanisms of functional integrals of quantum field theory, although
such calculations are considerably more abstract, and thus difficult
to comprehend. In addition, they can be carried out only for the
simplest of geometries.
However, the formalism of quantum field
theory makes it clear that the vacuum expectation value summations
are in a certain sense summations over so-called "virtual
particles".
More interesting is the understanding that the sums over
the energies of standing waves should be formally understood as sums
over the eigenvalues of a Hamiltonian. This allows atomic and
molecular effects, such as the van der Waals force, to be understood
as a variation on the theme of the Casimir effect.
Thus one
considers the Hamiltonian of a system as a function of the
arrangement of objects, such as atoms, in configuration space. The
change in the zero-point energy as a function of changes of the
configuration can be understood to result in forces acting between
the objects.
In the chiral bag model of the nucleon, the Casimir
energy plays an important role in showing the mass of the nucleon is
independent of the bag radius. In addition, the spectral asymmetry
is interpreted as a non-zero vacuum expectation value of the baryon
number, cancelling the topological winding number of the pion field
surrounding the nucleon.
Casimir effect and wormholes
Exotic matter with negative energy density is required to stabilize
a wormhole. Morris, Thorne and Yurtsever pointed out that the
quantum mechanics of the Casimir effect can be used to produce a
locally mass-negative region of space-time, and suggested that
negative effect could be used to stabilize a wormhole to allow
faster than light travel. This concept has been used extensively in
Science Fiction.
Analogies
A similar analysis can be used to explain Hawking radiation that
causes the slow "evaporation" of black holes (although this is
generally visualized as the escape of one particle from a virtual
particle-antiparticle pair, the other particle having been captured
by the black hole).
Repulsive forces
There are few instances wherein the Casimir effect can give rise
to repulsive forces between uncharged objects. In a seminal paper,
Evgeny Lifshitz showed (theoretically) that in certain circumstances
(most commonly involving liquids), repulsive forces can arise. This
has sparked interest in applications of the Casimir effect toward
the development of levitating devices.
Other scientists have also
suggested the use of gain media to achieve a similar levitation
effect, though this is controversial because these materials seem to
violate fundamental causality constraints and the requirement of
thermodynamic equilibrium. An experimental demonstration of the Casimir-based levitation was recently demonstrated by the Capasso
group at Harvard through experiments involving a gold-coated
particle and silica thin film immersed in bromobenzene.
Applications
It has been suggested that the Casimir forces have application in
nanotechnology, in particular silicon integrated circuit technology
based micro- and nanoelectromechanical systems, and so-called
Casimir oscillators.
Classical 'Critical' Casimir Effect
In 2008, physicists in Germany made the first direct
measurements of the “critical Casimir effect”, a classical analogue
of the quantum Casimir effect. This effect had been theoretically
predicted in 1978 by Michael Fisher and Pierre-Gilles de Gennes but
all observations had been indirect.
In this experiment, the critical Casimir effect arises in a mixed
liquid that is close to its critical point. The liquid used was a
solution of water and the oil 2,6-lutidine which has a critical
point of 34°C at normal atmospheric pressure. As this liquid
approaches its critical point, the oil and water starts separate
into small regions whose size and shape are subject to statistical
fluctuations and that exhibit random Brownian motion.
To demonstrate
the effect, a tiny coated Styrofoam ball is suspended in the liquid
close to the wall of its coated glass container. The ball and the
container coatings are the same and both have a preference for
either oil or water. As the liquid nears its critical point, total
internal reflection microscopy is used to detect displacements of
the ball.
From the sudden movements detected only towards the glass,
the classical Casimir force was calculated to be approximately 600
fN (6 x 10−13 N). To tune the effect for repulsion, the coatings of
the glass and the ball are changed so that one prefers oil and the
other water.
While the German physicists say this reverse critical Casimir effect
could be useful in nanoelectromechanical systems, its dependence
upon a very specific temperature presently limits its usefulness.
Back to Contents
|