|
3 -
Dark (Missing) Matter
What Was Missing
Dutch astronomer Jan Oort first discovered the 'missing matter'
problem in the 1930's. By observing the Doppler red-shift values of
stars moving near the plane of our galaxy, Oort assumed he could
calculate how fast the stars were moving. Since the galaxy was not
flying apart, he reasoned that there must be enough matter inside
the galaxy such that the central gravitational force was strong
enough to keep the stars from escaping, much as the Sun's
gravitational pull keeps a planet in its orbit.
But when the
calculation was made, it turned out that there was not enough mass
in the galaxy. And the discrepancy was not small; the galaxy had to
be at least twice as massive as the sum of the mass of all its
visible components combined.
Where was all this missing matter?
In addition, in the 1960's the radial profile of the tangential
velocity of stars in their orbits around the galactic center as a
function of their distance from that center was measured. It was
found that typically, once we get away from the galactic center all
the stars travel with the same velocity independent of their
distance out from the galactic center. (figure below.)
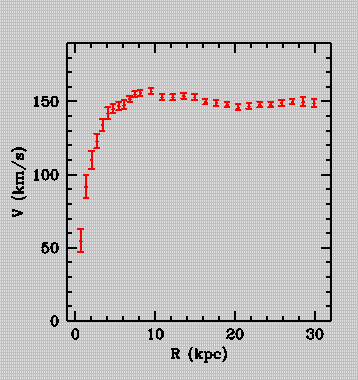
Figure 1.
A typical star's tangential velocity as a function of its
distance from the galactic center.
Usually, as is the case with our solar system, the farther out an
object is, the slower it travels in its orbit.
To visualize the seriousness of the problem cosmologists face, we
need to consider just a bit of Newtonian dynamics:
To change a body's velocity vector - either in direction or
magnitude or both, a force must be applied to the mass of the body.
The resulting acceleration is equal to the ratio of the applied
force divided by the mass of the object; i.e., f = m a, where f is
the force applied to the body, m is the mass of the body, and a is
the resulting acceleration (change in velocity).
Both f and a are
vectors; the change in direction of the velocity will be in the
direction of the applied force.
When an Olympic athlete, starting to do the hammer throw, swings the
hammer around himself in a circle, the force he feels stretching his
arms (the force he is applying to the hammer) is the 'centripetal
force'.
That force is equal to the product of the hammer's mass, m1,
times the centripetal acceleration (which in this case is the
acceleration that continually changes only the direction, not the
magnitude, of the velocity vector of the hammer - inward - so as to
keep it in a circular orbit around the athlete).
This acceleration
is equal to the square of the hammer's tangential velocity, v,
divided by the radius of the circle. So, the inward force the
athlete needs to exert to keep the hammer in its circular path is: f
= m1 v2/R.
Newton's law of gravitational force says that the force between two
masses is equal to G (the gravitational 'constant') times the
product of the two masses divided by the square of the distance
between them. f = G(m1 x m2)/R2.
Consider the case of a star on the outskirts of a galaxy. Its radius
from the galactic center is R. Its mass is m1, and m2 is the total
mass of everything else (all the other stars and matter) inside a
circle whose radius is R, the distance of the star from the galaxy's
center. Newtonian dynamics assumes all that combined mass, m2, acts
as if it were located at a single point at the galaxy's center.
For
the star to remain in a fixed orbit, the necessary inward
(centripetal) force, m1 V2/R, must be exactly equal to the
available (gravitational) force, G(m1 x m2)/R2.
Setting these two
expressions equal to each other results in the expression:
m2 = (V2) R /G
This says that for the tangential velocity, V, to remain constant as
R increases - as it does in figure 1 (as we look at stars farther
and farther out from the galaxy's center) the included mass, m2,
must increase proportionally to that radius, R. But we realize that,
if we move far out from the center, to the last few stars in any
galaxy, included mass will not increase proportionally to the
radius.
So there seems to be no way the velocity can remain the same
for the outermost stars as for the inner stars. Therefore,
astrophysicists have concluded that, either some mass is 'missing'
in the outer regions of galaxies, or the outer stars rotating around
galaxy cores do not obey Newton's law of gravity.
There were problems, too, at a larger scale. In 1933 astronomer
Fritz Zwicky announced that when he measured the individual
velocities of a large group of galaxies known as the Coma cluster
(click below image),
he found that all of the galaxies that he measured were moving so
rapidly relative to one another that the cluster should have come
apart long ago.

The visible mass of the galaxies making up the
cluster was far too little to produce enough gravitational force to
hold the cluster together.
So not only was our own galaxy lacking
mass, but so was the whole Coma cluster of galaxies.
MACHOs, WIMPs & MOND
At first, cosmologists decided to leave Newton's laws inviolate and
to postulate the existence of some invisible dark entities to make
up the missing mass. Apparently it never occurred to anyone to go
back and examine the basic assumption that only gravity was at work
in these cases. It was easier to patch up the theory with invisible
entities. (Remember the invisible gnomes in my garden?)
To quote
Astronomy magazine (Aug. 2001 p 26):
"What's more, astronomers have gone to great lengths to
affectionately name, define, and categorize this zoo of invisible
stuff called dark matter. There are the MAssive Compact Halo Objects
(MACHOs) - things like ... black holes, and neutron stars that
purportedly populate the outer reaches of galaxies like the Milky
Way. Then there are the Weakly Interacting Massive Particles
(WIMPs), which possess mass, yet don't interact with ordinary matter
- baryons such as protons and neutrons - because they are composed
of something entirely foreign and unknown.
Dark matter even comes in
two flavors, hot (HDM) and cold (CDM)....."
-
Cold dark matter - supposedly in dead stars, planets, brown
dwarfs ("failed stars") etc.
-
Hot dark matter - postulated to be fast moving particles floating
throughout the universe, neutrinos, tachions etc.
"And all the while astronomers and physicists have refined their
dark matter theories without ever getting their hands on a single
piece of it. But where is all of this dark matter? The truth is that
after more than 30 years of looking for it, there's still no
definitive proof that WIMPs exist or that MACHOs will ever make up
more than five percent of the total reserve of missing dark stuff."
Of course, the second possibility mentioned above (that the outer
stars rotating around galaxy cores do not obey Newton's Law of
Gravity) was thought to be impossible. But the first alternative -
the fanciful notion that 99% of the matter in the universe was
invisible - began to be worrisome too.
It was stated that WIMPs and
MACHOs were in the category of particle known as "Fabricated Ad hoc
Inventions Repeatedly Invoked in Efforts to Defend Untenable
Scientific Theories" (FAIRIE DUST).
Even such an august authority as
Princeton University cosmologist Jim Peebles has been quoted as
saying,
"It's an embarrassment that the dominant forms of matter in the
universe are hypothetical..."
So the second alternative, radical as it is, was chosen by some
astrophysicists and called "MOdify Newton's Dynamics" (MOND) This
paradigm shaking proposal to alter Newton's Law of Gravity - because
it does not seem to give correct answers in the low density regions
of galaxies - was first put forward in 1983 by astrophysicist
Mordehai Milgrom at the Weizman Institute of Science in Israel.
It
has recently been given more publicity by University of Maryland
astronomer Stacy McGaugh. Milgrom, himself, has recently ("Does Dark
Matter Really Exist?", Scientific American, Aug. 2002, p. 42-52)
said,
"Although people are right to be skeptical about MOND, until
definitive evidence arrives for dark matter or for one of its
alternatives, we should keep our minds open."
One wonders what
alternatives was he referring to?
Some other astrophysicists have grasped at the announcement that
neutrinos, that permeate the cosmos, have mass. This, they say, must
be the previously "missing matter". But the "missing mass" is not
missing homogeneously throughout the universe - just in specific
places (like the outer reaches of galaxies). The neutrinos are
homogeneously distributed. So this last ditch explanation fails as
well.
The dilemma presented by the fact that Newton's Law of Gravity does
not give the correct (observed) results in most cases involving
galaxy rotation can only be resolved by realizing that Newton's Law
of Gravity is simply not applicable in these situations. Galaxies
are not held together by gravity.
They are formed, driven, and
stabilized by dynamic electromagnetic effects.
The Real Explanation -
Dynamic Electromagnetic Forces in Cosmic Plasmas
Ninety nine percent of the universe is made up of tenuous clouds of
ions and electrons called electric plasma. Plasmas respond to the
electrical physical laws codified by James Clerk Maxwell and
Oliver
Heaviside in the late 1800's.
An additional single law due to
Hendrick Lorentz explains the mysterious stellar velocities
described above.
d/dt(mv) = q(E + v x B)
Simply stated, this law says that a moving charged particle's
momentum (direction) can be changed by application of either an
electric field, E, or a magnetic field, B, or both. Consider the
mass and charge of a proton for example. The electrostatic force
between two protons is 36 orders of magnitude greater than the
gravitational force (given by Newton's equation).
It's not that
Newton's Law is wrong. It is just that in deep space it is totally
overpowered by the Maxwell-Lorentz forces of electromagnetic
dynamics.
Notice, in the equation in the previous paragraph, that the change
in a charged particle's momentum (left hand side of the equation) is
directly proportional to the strength of the magnetic field, B, the
particle is moving through. The strength of the magnetic field
produced by an electric current (e.g., a cosmic sized Birkeland
current) falls off inversely as the first power of the distance from
the current.
Both electrostatic and gravitational forces fall off
inversely as the square of the distance. This inherent difference in
the spatial distribution of electromagnetic forces as compared to
gravitational forces may indeed be the root cause of the
inexplicable velocity profiles exhibited by galaxies.
Electrical engineer Dr. Anthony L. Peratt, using Maxwell's and
Lorentz's equations, has shown that charged particles, such as those
that form the intergalactic plasma, will evolve into very familiar
galactic shapes under the influence of electrodynamic forces. The
results of these simulations fit perfectly with the observed values
of the velocity contours in galaxies. No missing matter is needed -
and Newton can rest easy in his grave.
The electromagnetic force is
many orders of magnitude stronger than the force due to gravity and
it distributes itself more widely throughout space. But present day
astronomy refuses to recognize the existence of any cosmic force
other than gravity. That error is the cause of their mystification.
An allegory:
A farmer and his young daughter are driving along a dusty road. They
are almost home when the car breaks down. The farmer walks to the
barn and gets his horse, Dobbin. He harnesses Dobbin to the front
bumper of the car and begins to drag it along the road toward home.
The young daughter takes a piece of string and attaches it to the
bumper and says, "I'll help drag the car, Daddy."
Anyone who cannot see horses will think the daughter must possess
"missing muscle".
Or, as in Moti Milgrom's
MOND proposal, they might suggest that
Newton's Laws of motion needed "modification" in this case.
In 1986, Nobel laureate Hannes Alfven postulated both an electrical
galactic model and an electric solar model. Recently physicist Wal
Thornhill has pointed out that Alfven's circuits are really scaled
up versions of the familiar homopolar motor that serves as the
watt-hour meter on each of our homes. The simple application of the
Lorentz force equation ("crossing" the direction, v, of the current
into the direction, B, of the magnetic field) yields a rotational
force.
Not only does this effect explain the mysterious tangential
velocities of the outer stars in galaxies, but also (in scaled down
version) the observed fact that our Sun rotates faster at its
equator than at higher (solar) latitudes.
Up to now astronomers and cosmologists have not given serious
consideration to any sort of electrical explanation for any of the
above observations. This is puzzling because all these electrical
principles have now been known for decades. They have long been
applied in the solution of problems in plasma laboratories here on
Earth and have been used successfully in the invention of many
practical devices - such as industrial electrical arc machining,
particle accelerators, etc.
The correct, simple, solution to the
"mysteries" of galaxy rotation lies in Plasma Electro-Dynamics - not
in the invention of imaginary, fanciful entities such as WIMPs and
MACHOs or in the trashing of a perfectly valid law of physics as is
proposed in MOND.
Conclusion
Present day astronomy/cosmology seems to be on the horns of a very
painful dilemma. This dilemma is caused by the fact that Newton's
Law of Gravity does not give the correct (observed) results in most
cases involving galaxy rotation. The "missing matter" proposal
attempts to balance the equation by increasing one of the variables
(one of the mass terms). The second proposal (MOND) is to change
Newton's equation itself. (If you are losing the game, change the
rules.)
But, the ultimate resolution of the dilemma lies in realizing that
Newton's Law of Gravity is simply not applicable in these
situations.
Maxwell’s equations are!
Why do astrophysicists grope
wildly for solutions in every possible direction except the right
one?
Back to
Contents
|

