Chapter 8 - Current Sheets, Perpendicular Currents and Electric Circuits
January 17, 2012

8.1 Plasma Current Sheets

Reference has already been made to the filamentation of current sheets.

This section will explore the nature of current sheets and their relationship to the magnetic field. A current sheet is exactly what it says - a thin surface within which a current flows.

It obviously differs from a diffuse cloud of moving charge and from a cylindrical filament of current. A current sheet forms a surface between two regions of plasma, somewhat like a Double Layer, and, also like a DL, often separates regions of different characteristics.

The current in the sheet flows in one direction, contained entirely within the sheet. One can think of it as though the current was flowing in the warp threads of a woven linen sheet: all the current flows in the same direction in each of the warp threads, and no current flows in the weft threads. A current, of course, consists of ions and electrons flowing in opposite directions, so the current sheet will contain both types of particle.

Obviously the direction of the current can change as the sheet itself does not need to be planar.

For example, there is clear evidence of a part-spherical current sheet at the 'bow shock' where the Earth's magnetosphere interacts with the incoming solar wind.
 

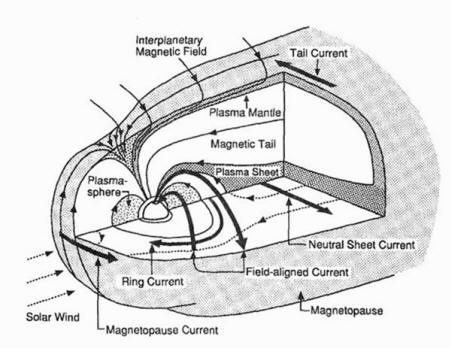
Depiction of Earth's magnetospheric plasma current sheets
Credit - Wikipedia Images, numerous websites without attribution
 

If we analyze the magnetic field near a current sheet we find that the magnetic force due to the current sheet is in opposite directions on either side of the sheet.

For example, if a current is flowing up this page, then above the page the magnetic field will be from left to right, and below the page it will be from right to left, as one would expect from the rotation right-hand rule for any individual 'thread' of current. (Note that the rotation right hand rule is not the same as the vector cross-product right hand rule !)

Thus a principal effect of a current sheet is to create separate areas of opposing magnetic fields. At the sheet location itself, the magnetic field is zero.

This is exactly the situation that has been found in the tail area of the Earth's magnetosphere, where a current sheet in the equatorial plane separates zones of opposing magnetic field. In this case, the tail sheet current flows azimuthally or 'west to east' and the magnetic fields are radial, being aligned towards the Earth in the Northern hemisphere and away from the Earth in the Southern hemisphere.

The Gravity Model describes these current sheets as caused by the opposing magnetic fields on either side. Remembering that magnetic fields are force fields that are caused by the motion of charged particles, that is, currents, the Gravity Model appears to be inverting cause and effect.

What the magnetic fields created by the current actually do is to compress the current into the form of a sheet. They do not create the current.

Current sheets therefore are another means by which plasma can cellularize in response to differing environments. Current sheets can also act to accelerate mass in a pulsed plasma thruster application.

See text and video from Princeton University's Electric Propulsion and Plasma Physics Lab here.
 

8.2 Perpendicular Currents

We have already considered the cases where currents flow parallel to (are "field-aligned with") the magnetic field (filaments and Birkeland Currents) and the case where currents flow in regions of zero field (current sheets).

The remaining possibility is for currents to have a vector component that is perpendicular to the magnetic field under the influence of nonmagnetic forces acting in combination with the magnetic field (see 8.3 below).

[Recall that F is the resulting force vector on a charged particle; q is the value of the amount of charge on the particle; E is the electric field's vector value at a specified time and coordinate; U is the velocity vector of the charged particle at that time and coordinate, and B is the magnetic field vector at that time and coordinate. Finally, note that the bold vectors refer to a scalar magnitude value plus a direction, e.g., 3000 km/s heading east.]

The Lorentz Force on a charged particle, F = q(E + U × B) in vector algebra, depends on the relationship of the velocity of the particle U to the magnetic field B.

The magnitude of the vector cross product U × B can be written UB sin θ, where θ is the smaller angle between U and B. The direction of the force produced by U × B is given by the movement of a right-handed screw turned from U to B, that is, it is at right angles to both U and B.

This causes a charged particle moving at right angles to the magnetic field to follow a circular path in a plane perpendicular to the field. We can call this the centripetal force. If E is nonzero, the particle will also accelerate in the direction of E.

Obviously, if U is zero or parallel to B then there is no centripetal force on the particle from the magnetic field. In other words, if the particle is stationary or moving parallel to the field, then it will experience no magnetic force.

Rather than considering variable angles between U and B, it is easier to consider the parallel and perpendicular components of U separately. As only the perpendicular component causes a force, we shall concentrate on that component alone. We shall also assume E = 0 unless stated otherwise.

The particle velocity that would result from a combination of a force-induced motion and a magnetic field can be considered as a circular motion around a guiding center (image below), which center itself drifts perpendicular to the magnetic field with velocity vp given by the Guiding Center Equation:

vp = (F × B) / qB2

Note that F is any nonmagnetic force (for example, gravity, or an electric field) which causes motion of a charged particle. This motion then interacts with the magnetic field according to Lorentz's Law.

When B is in the z direction and F is in the y direction in Cartesian coordinates, then the resulting velocity vp is in the x direction.
 

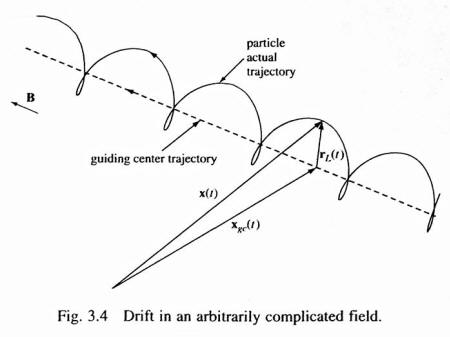
Helical trajectory of a charged particle,

with its circular motion superimposed on its drift velocity vector.

Image credit:

"Fundamentals of Plasma Physics", Cambridge Press, 2006;

Dr. Paul Bellan, California Institute of Technology
 

What this equation tells us is that, when a particle is subject to an external force perpendicular to the magnetic field, it will acquire a constant velocity vp perpendicular to both the field and the force.

How this comes about is as follows:

If a particle is initially at rest, an external force (an electric field, say) will start to accelerate it in the direction of the force according to Newton's laws. However, as soon as the particle acquires some small amount of velocity or velocity component perpendicular to the magnetic field, then a centripetal force emerges as a result of the magnetic field and starts to turn the path of the particle away from the trajectory induced by the external force.

The external force is still trying to accelerate the particle in the direction of the force, but there is now a component of the centripetal force which opposes the external force. The acceleration in the direction of the external force will be reduced accordingly.

Under the influence of the twin external and centripetal forces, the particle will follow a curved path turning through 90 degrees.

 

At the point when the path is perpendicular to the external force, the particle has acquired the velocity vp given by the Guiding Center Equation, and the centripetal force due to the interaction of vp and B exactly balances the external force.

Therefore, there will be no more acceleration in the direction of the external force, nor will there be any acceleration in the direction of vp because there is no force in that direction. The particle has acquired a constant velocity perpendicular to both B and the external force.

As long as the particle continues to move with velocity vp in the perpendicular direction, then the situation is stable, and the external force remains balanced by the centripetal force.

8.3 Effect of Various External Forces

The above discussion applies to any constant external force acting on a charged particle in a magnetic field. Various forces can cause velocities in the direction perpendicular to the magnetic field.

These include gravity, an electric field, and inertial forces.

Each will have a different effect dependent on whether the external force is a function of the mass of, or the charge on, the particle, as follows:

Case A. Electrical Field Force, FE × B for an electric field perpendicular to B.

Because FE = qE, the Guiding Center Equation becomes:

vp = (E x B) / B2

In Case A, the perpendicular velocity is independent of the charge on the particle.

This results in the special case of ions and electrons both drifting in the same direction, as we saw when considering the concentration of matter by filamentary currents.

Case B. Gravity, Fg×B

Because Fg = mg , the resulting perpendicular drift velocity is dependent on both the mass of the particles and their charge, and for Case B:

vp = (g × B) × m/qB²

Ions and electrons will therefore move in opposite directions, resulting in a current, charge separation, and zones of different potential (i.e., electric fields).

All these effects will occur simply as a result of the interaction of gravity and a magnetic field. Obviously these effects will then start to cause secondary effects of their own, and complex plasma behavior can result. (Ref: Fundamentals of Cosmic Electrodynamics, Boris V. Somov, Kluwer Academic Publishers, 1994, Chapter 2, Motion of a Charged Particle in Given Fields)

In addition, the dependence of the velocity on the mass of the particles can also result in chemical separation of different ions, or Marklund Convection.
One case in particular is of interest here.

Consider the Earth and its magnetic field, which can be visualized as field lines spreading out into near space arranged somewhat like the segments of an orange. In the equatorial plane, the field will be aligned north-south. The gravitational force will be radially inwards and so at right angles to the field.

Any ions and electrons in the vicinity, for example, in the ionosphere, will therefore acquire velocities perpendicular to both B and g under the combined influence of gravity and the magnetic field. Because the velocities of ions and electrons are in opposite directions, this is equivalent to a current flowing in a ring around the equatorial plane.

The Van Allen belts are examples of ring currents.

This is an inevitable result of the presence of charged particles in a magnetic field orientated at right angles to the gravitational field. A current will always be generated in this situation.

Several of the moons of Jupiter and Saturn exhibit these currents, evidenced by the electromagnetic radiation where the induced currents come in contact with the planets' atmospheres in the vicinity of their polar auroral ovals.

Case C. Inertia, Fi = -m (du/dt) (Newton's Second Law of Motion)

In this case the charged particles already have an initial momentum mu (inertial mass times the velocity vector) when they encounter a magnetic field.

The Guiding Center Equation indicates that the initial momentum will be altered by the magnetic field:

vp = -mq/B² du/dt × B

As vp is charge-dependent, the final velocity of ions and electrons is in opposite directions and therefore represents a current.

Ions of different masses will acquire different final velocities and so will be chemically sorted. There is also another important effect of inertial effects:

If a volume of plasma is accelerated to a particular velocity due to, for example, an I × B force in the region (which accelerates oppositely moving ions and electrons in the same perpendicular direction), then the plasma has acquired kinetic energy at the expense of the circuit driving the current.

If this volume of moving plasma then enters another region where it can establish a circuit in the local plasma, its velocity vp will cause a current perpendicular to both B and vp .

The interaction of this current with B will cause a force on the moving plasma which slows it down. In other words, the plasma's kinetic energy is given up again in generating a current in a new location.

Therefore the interaction of the inertial motion of charged particles and a magnetic field is a means by which kinetic energy can be exchanged with electromagnetic energy, and therefore it is a means by which energy can be transported between different locations.
 

8.4 Electrical Circuits in Plasma

Unless charge is flowing from an electrostatic source or to a sink, then it will form part of a closed circuit.

In space, the circuit may not always be obvious because the conductors are often invisible and may close the circuit at vast distances from the areas of interest, but they must close somewhere.

Consideration of the circuits in space can explain behavior such as transport of energy from one area to another which drives detectable electrical activity in a region under investigation.

In this context, it is worth pointing out that if a plasma containing any regions of slight charge imbalance is moving relative to another region of plasma in a magnetic field, then the first region will induce an electric field and currents in the second region due to the interaction of the electromagnetic fields and forces.

The Gravity Model holds that Debye screening, which is due to similar effects as cause a Debye sheath around a charged body, limits the extent of charge imbalances to the Debye length.

However, the v × B force from the Lorentz equation is independent of the Debye length and can induce an electric field in another region of plasma well beyond the Debye limit.

8.5 Double Layers as Circuit Elements

Any Double Layer (DL) accelerates ions and electrons due to the potential drop across the DL.

If the DL is a current-carrying DL, then it effectively forms part of an electrical circuit in which the current is flowing. The energy to accelerate the particles is supplied by the circuit and converted within the DL into kinetic energy.

The DL therefore acts as an inertial resistance and may experience a reaction which causes its position to drift.

This is analogous to the recoil of a gun as its power source accelerates the mass of the bullet. Particles accelerated by the DL cause a pressure on the surrounding plasma, with which they interact and cause radiation.

Dissipation of excess energy in this fashion can allow the plasma to reach a stable state via the formation of a DL which provides the necessary mechanism.

8.6 Energy and Inductance

The circuit energy supplied to the DL may originate in the energy stored in the magnetic field or in the kinetic energy of the bulk plasma.

In circuit terms, an element which stores energy is an inductor. The plasma may therefore be thought of as analogous to an inductor in a simple circuit. Similarly, the DL behaves in some respects as a capacitor, although one with variable characteristics, including a resistance which can reduce with increasing current.

All electrical circuits which have inductance are potentially unstable, depending on the values of voltage, inductance, resistance, and capacitance around the circuit.

If the total resistance of the circuit is negative, which is often the case in plasma because of the falling characteristic of the I-V (current versus voltage) curve, then stability of the inductive circuit is impossible. A simple circuit involving voltage, inductance, and negative resistance will either oscillate or dissipate all its energy and become extinct.

If the potential drop across the DL is larger than the plasma potential, then the DL is classified as a strong DL.

A strong DL will reflect particles that approach the DL with energies less than the plasma potential. Only those particles with energies above the plasma potential will enter the DL and be accelerated by its voltage differential, i.e., electric field.

The behavior of plasma in a CCDL is thus dependent on the characteristics of the external circuit which is driving the formation of the CCDL.
 

8.7 Resonant Circuits

A circuit containing inductance and capacitance has a natural or resonant frequency at which it will oscillate electrically.

Similarly, a plasma circuit containing inductance in the form of stored magnetic energy and a CCDL exhibiting negative resistance will tend to have a resonant frequency at which energy is exchanged between the electric field in the DL and the magnetic field in the plasma. As the electric field in the DL increases, it will accelerate particles to higher energies in the normal manner.

It is apparent that this model is an efficient means of generating high-frequency bursts of radiation. By contrast, the Gravity Model postulates very high density neutron stars rotating up to thousands of times a second in order to explain this commonly-observed phenomenon.

Not all situations result in a resonant frequency. Variations often result in oscillations over a wide frequency band. The DL is then 'noisy' in electrical circuit terms. The effect of the noise is to create a range of electron energies in the beam accelerated by the DL.

Some electrons then have enough energy to break out of the magnetic field confining the current, and this can lead to expansion of the plasma.

Back to Contents





Chapter 9 - Plasma Circuit Instabilities
February 26, 2012

9.1 Exploding Double Layers

The inductive energy of a circuit is a function of the current and the inductance.

If any inductive circuit is disrupted, for example, by opening a switch, then the inductive energy of the circuit will be released at the point of disruption.

In a plasma circuit, current disruption is often caused by the DL becoming unstable.

When that occurs, the entire inductive energy of the circuit is released in the DL. This can cause the DL to explode, resulting in extremely large voltage drops across the expanding DL and dissipation of prodigious amounts of energy, ultimately as heat and radiation as accelerated particles interact with other matter.

This behavior will occur under a constant magnetic field. The field plays no part in the explosion.

If the underlying current is still present after the explosion, then the cycle can repeat indefinitely.

A DL forms, the current increases, the DL explodes with consequent emission of large amounts of radiation, the current starts to build up again, and a new DL forms. It is obvious that this type of behavior cannot be described using field-based models.

Current-based models are essential in order to capture this level of complexity.

9.2 Expanding Circuits

The energy from an inductive circuit can also be released by explosive expansion of a loop of current due to the forces generated by the loop current itself.

We have already seen how an axial current causes a pinching magnetic force. The opposite situation is a loop current which generates an axial magnetic field. In this case, the resulting I × B force is radially outwards.

If the outward pressure is not balanced by other forces, then the current loop itself will expand. In a metal conductor, the balancing force is provided internally by the metal lattice structure itself.

In a plasma, there may be insufficient restraint, especially if the inductive energy of the circuit is being released in a short period due to collapse of a DL in the circuit.

This can result in an explosion of the current loop, such as is often seen in solar Coronal Mass Ejections (CME), where a loop of current rapidly expands away from the surface of the Sun. This simple explanation based on known electrical behavior contrasts with the Gravity Model, which invokes "magnetic reconnection" of lines of magnetic force.

As magnetic lines of force do not exist in a physical sense any more than lines of latitude do, it is hard to see how they can 'break' and 'reconnect' and release energy.
 

9.3 Other Filamentary Instabilities

Filamentary currents are subject to a pinch force, as we have seen.

However the simple pinch is itself unstable in a number of circumstances. If the pinch force increases and causes a contraction, this results in a further increase in the pinch force. The current filament can become so constricted that it forms into a series of bulges and constrictions like a string of sausages.

Photo of kink or "sausage" instability in one of the earliest plasma z-pinch devices, a Pyrex tube used by the AEI team at Aldermaston, UK, circa 1951/52 - public domain

If the axial current is strong enough, then the pinches can eventually collapse completely. In this case, the axial current is diverted into a ring current in the pinched zones, and donut-shaped magnetic plasmoids develop along the line of the filament. If matter has already been concentrated into the filament then this matter will be distributed along the line of the field-aligned current like pearls on a string.

This could explain many linear alignments of bodies in space.
 

Another form of instability is the kink instability.

This occurs most often in Birkeland Currents, where the current is aligned with the external magnetic field. The pinch then develops a strong helical mode. The effect is to offset the current cylinder relative to the field direction.

This can appear as a kink in the current when viewed from the appropriate angle.
 

9.4 Peratt Instabilities

Recent research by Anthony Peratt as reported in the IEEE journals and other academic institutions has identified a series of very high energy plasma discharges which now bear his name. Here is a representative paper by Peratt and Van Der Sluijs.

The Peratt Instabilities are modes of plasma discharge which adopt definite forms and which, despite their name, can remain stable for periods of time long enough to observe them. In some respects, they are like DLs, which are dynamic 'instabilities' that can remain static in location whilst involving rapid particle motions.

The Peratt Instabilities often take the form of a columnar plasma discharge which is surrounded by stacked plasma toroids.

The top and bottom toroids can evolve into cup and bell shapes. The edges of the toroids often warp upwards or downwards. The number of toroids can vary between three and around nine and can resemble anything from chalices to ladders.

Various other forms exist as well, depending on the nature of the plasma and the currents in it.

Peratt's research into plasma phenomena at many scales has led him to suggest that it may be likely that rock art created in relatively recent history may be recordings of the sightings of a particular form of plasma discharge with attendant characteristic instability forms and shapes, as outlined in his graphically stunning IEEE paper, Characteristics for the Occurrence of a High-Current Z-Pinch Aurora as Recorded in Antiquity, IEEE Transactions on Plasma Science, Vol. 31, No. 6, December 2003.

The point to be made here is that none of these forms of plasma instabilities could possibly be predicted by an analysis based on magnetic fields, yet particle-in-cell computer simulations do yield the same results.

Once again we see that plasma behavior is often too complicated to be described by magnetohydrodynamic, or MHD, fluid equations. It is necessary to base the analysis on the movements of particles, that is, a current-based solution.
 

Back to Contents





Chapter 10 - Rotational Effects
February 29, 2012

10.1 Rotation and Faraday Motors

One of the reasons for the assumption of large amounts of Cryogenic (or Cold) Dark Matter (CDM) in the Gravity Model is to explain the observed rotation of galaxies.

Astronomers have found that the individual stars in galaxies do not orbit the center of the galaxy in accordance with Kepler's Laws for the motion of the planets.

More specifically, the stars outside the central bulge of a galaxy all have approximately the same angular velocity, rotating more like a rigidly connected disk, but according to Kepler's laws, the velocity should be less as distance from the center increases.

Adding a large quantity of Dark Matter in a halo around each galaxy could modify the gravitational force sufficiently to make the stars behave in the way they do.

This is now accepted as part of the Standard Model in astrophysics.

Dark matter itself has never been directly observed or handled in a lab setting. It is dark, after all, by definition; and by definition only interacts via the gravitational force with "normal" observable matter. However, there is another way stars could be made to orbit a galaxy in this fashion.

Michael Faraday found (circa 1831-1832, from The Electric Life of Michael Faraday by Alan Hirshfeld, Walker & Co., 2006) that a metal disk rotating in a magnetic field aligned with the axis of the disk would cause an electric current to flow radially in the disk, so he invented the first generator, known as a Unipolar Inductor, or Faraday Generator.

The effect eventually was proved to be a result of the Lorentz Force acting on the electrons in the disk as they moved across the magnetic field.

If the current is supplied by an external circuit, the disk is made to rotate by the same force now acting on the electrons in the current.

Of course the rotational velocity of the disk sets up different forces which oppose the driving current, and a balance is reached between the two. This arrangement is known as a Faraday Motor.

Galaxies are known, through precise Faraday rotation measures (RM) of the polarization of the light they emit, to possess magnetic fields aligned with their axes of rotation, and they also have conducting plasma among their stars.

Assuming that currents exist in the plane of the galaxy similar to the equatorial current sheet known to exist in the Solar System, then the conditions appear to be similar to that in a Unipolar Inductor or Faraday Motor. Of course the disk in this case is not rigid.

The exact mode of rotation would depend on the balance between the radial driving current and the rotationally induced opposing current, as in a Faraday Motor, but it is at least possible that it is these electrical effects that are causing the anomalous rotation that we see, not some huge quantity of invisible Dark Matter.

In this context, it is interesting to see the recent discovery by the Sloan Digital Sky Survey of a ring of stars in the equatorial plane of the Milky Way but outside our galaxy.

The similarity with a toroidal current around a pinch in a large Birkeland Current along the axis of the Milky Way suggests that once again electrical forces on a galactic scale may be responsible for the formations we see.

Structures similar to Faraday Motors have been observed in nebulae as well. One of the most obvious examples is in the Crab Nebula, where the Chandra X-ray image demonstrates very clearly all the required elements of an inductor or motor arrangement.
 

10.2 Spiral Galaxies and Birkeland Currents

Anthony Peratt, who was mentioned above, has also carried out particle-in-cell computer simulations of interacting Birkeland currents.

He found that the shape and rotational characteristics of spiral galaxies, including barred spirals, which are a very common form in space, arise naturally from the interplay of electromagnetic forces in large Birkeland currents.

This result may help explain the origin of rotational energies in galaxies, which gravity-based theories find hard to do.

Back to Contents





Chapter 11 - Radiation
March 30, 2012

11.1 Light

Visible light ranges from red through yellow and green to blue and violet.

Newton was the first to discover that white light is a mixture of all the colors. White light can be split into its component colors by diffraction through a prism, which 'bends' each color by a different amount.

A diffraction grating is often used in astronomy because tiny or dim light sources suffer less energy loss in reflecting from a hard, ruled surface than is lost traveling through a glass prism.

Eventually, Maxwell, who defined the Electromagnetic Field equations, proved that light was in fact made up of electromagnetic (EM) waves. Each color of visible light has a characteristic frequency and wavelength.

As with all waves, the product of frequency and wavelength give the velocity of the wave. Obviously, light travels at the velocity of light, but Maxwell was able use his equations to shown that all electromagnetic waves travel with the velocity of light, and so light must also be an electromagnetic wave.

Visible light represents only a small part of all the possible frequencies or wavelengths.

The whole range is known as the electromagnetic spectrum.

11.2 The Spectrum

Although the spectrum is continuous, each region of the spectrum has been named after a typical type of wave for that part of the spectrum.

Starting with the lowest-frequency, longest-wavelength waves, the spectrum runs from,

• radio waves through microwaves (as in ovens)

• terahertz radiation (a recent development in military communications)

• infrared (as in heaters)

• the visible spectrum (Red, Orange, Yellow, Green, Blue, Indigo, Violet)

• ultraviolet (tanning and forensic lamps, materials analysis)

• X-rays (internal medical images)

• Gamma rays (cancer treatments)

The spectrum is shown in the following diagram. Note that the visible spectrum is only a small part of the whole spectrum.

When the Gravity Model was formulated, scientists could only see visible light from the heavens.
 

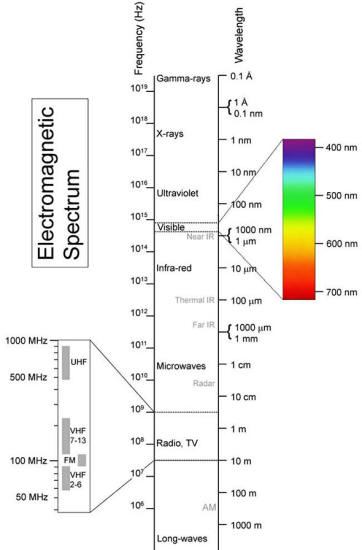
Diagram of the electromagnetic spectrum,

with images of the Crab nebula showing how it would "look"

if we could see beyond the limits of our eyes' light sensitivity range,

courtesy NASA
 

In the 20th century, and especially since the start of the Space Age in the 1950s, instruments have been developed which allow scientists to detect virtually all wavelengths. The amount of information available has increased exponentially.

Observations are often surprising because what is seen in the visible is seldom anything like what is found at other wavelengths.
 

Jupiter as seen in optical wavelengths (grayscale),

with its auroras radiating in invisible X-ray radiation

(mapped to visual violet as "false color" to appear visible to us).

Image credit: NASA / Chandra X-ray Telescope

11.3 Radiation

Radiation is the process whereby energy is emitted by one body, transmitted through a medium or through space, and eventually absorbed by another body. The emitting and absorbing bodies can be as small as individual atoms or even subatomic particles like electrons.

Electromagnetic waves are the means whereby the energy is transmitted. In other words, all radiation is electromagnetic.

This means that the mode of transmission of radiation involves oscillating electric and magnetic fields which carry the energy similar to the way that vibrations on a string carry energy along the string.

Since the speed of transmission of vibrational energy is constant for a given medium, and that value is equal to the frequency of the vibrating wave times the wavelength (frequency times wavelength = velocity), if you know the frequency one can solve for the wavelength at that frequency, and vice versa.

The spectrum represents the range of possible frequencies or wavelengths of the radiation.

As the frequency increases, the amount of energy carried by the wave also increases in proportion to the frequency. Ionizing radiation is radiation which carries sufficient energy to ionize atoms. In general terms, frequencies from radio to the visible do not carry enough energy for this, while ultraviolet, X-ray and Gamma ray radiation can ionize. As noted previously, ionization energy varies with different elements and molecules.

Radiation is emitted whenever a charged particle undergoes acceleration. Remembering that a change of direction is also an acceleration because the direction of the velocity is changing, then every charged particle that experiences a change of direction will emit radiation.

Current theories explain this emission in terms of the emission of a photon, or packet of energy. A photon has no mass but carries the radiated energy in the form of electromagnetic waves. A photon behaves both like a wave and like a particle. Which mode is more significant will depend on the circumstances.

To summarize:

• Radiation is emitted by all charged particles undergoing acceleration.

• All radiation involves electromagnetic waves.

• Radiation transmits energy.

• The spectrum represents the range of possible frequencies or wavelengths of the radiation.

11.4 Thermal radiation

Thermal radiation is radiation emitted from a surface of a body or region of particles due to the temperature of the body or region.

Temperature is a measure of the thermal energy contained in a body. The thermal energy causes the charged particles inside the atoms of the body to vibrate in a random fashion. They will therefore emit radiation over a range of frequencies. Similarly, a region of plasma can have a temperature.

A proportion of this radiation is emitted from the surface of the body or region as heat (infrared radiation). Actually, all matter with any internal thermal motion radiates EM energy: the colder it is, the longer the wavelength it radiates.

Cold interstellar dust will radiate terahertz, or sub-millimeter wavelength radiation, starting at a temperature of only about 10 Kelvin.

Because of the random nature of the vibrations over a large number of particles, the emitted radiation will have a range of frequencies, or wavelengths.

Statistical analysis shows that in an ideal situation the energy emitted at any one wavelength is a function of that wavelength. This is known as Planck's Law and is shown graphically below for a range of temperatures.

The radiation emitted in this ideal situation is known as Blackbody radiation, which simply means that it has the distribution pattern that would be expected from a perfect emitter in thermal equilibrium. (Diagram source: Wikipedia 'blackbody' article)
 

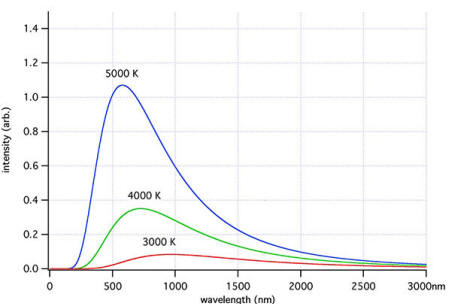
Ideal blackbody radiation for 3 temperatures,

showing that the peak wavelength emitted shifts

to higher frequencies (shorter wavelengths)

with increasing temperature.

Image credit: Wiki Commons
 

The graphs show that for any one temperature there is one wavelength at which the greatest amount of energy is emitted.

As the temperature increases, the wavelength of the peak energy decreases. This is defined by another law known as Wien's Law. Note that the red line has a lower temperature and lower area under its curve than the hotter blue line.

The area under any one temperature curve gives the total amount of energy emitted at that temperature, per unit area. The total energy emitted per unit area depends only on the temperature. This is known as the Stefan-Boltzmann Law.

If the pattern of emitted radiation from any source is distributed in the form given by Planck's Law, then the emission is assumed to be due to random thermal movements of particles in the source. We then say that the radiation is thermal radiation. All this means is that the radiation has a distribution of wavelengths or frequencies which come from the random thermal vibrations of particles.

The radiation itself is electromagnetic radiation like any other radiation.

If we find that radiation is thermal, then we can determine the temperature of the source by comparing the emitted radiation curve to the ideal 'Black Body' curves.

This means we can determine the temperature of distant objects if the radiation they emit is thermal radiation. Stars have been found to have a spectrum which approximates a blackbody distribution, so the color temperature of stars can be inferred from their spectra.

Non-thermal radiation is simply radiation which is not emitted in a thermal pattern. It must therefore be generated by other methods than random temperature-induced motions of the particles in a system in thermal equilibrium.

That is not to say that temperature cannot play a part in causing these other patterns of radiation; it is simply that the system or body that is emitting the radiation is not in thermal equilibrium. In other words, energy is being exchanged with the system so that its temperature is changing with time. This will alter the ideal Black Body pattern of radiation and mean that it is not possible to assign a temperature to the body.

Alternatively, the radiation may be emitted by individual particles undergoing acceleration caused by means other than random collisions with other particles.
 

11.5 Optical Radiation in the Cosmos

Radiation in the cosmos is common in the visible and radio wavelengths.

In the optical region, the majority of radiation is generated by electrons jumping to new orbits within an atom (bound-bound transitions), free electrons recombining with ions to form neutral atoms (free-bound transitions) and electrons being decelerated by interaction with other material (free-free radiation).

The bound-bound transitions are a source of both emission lines and absorption lines in the spectrum.

Each chemical element has a range of energies associated with the range of possible electron orbits around the nucleus for that element. As an electron jumps from one orbit to another, energy in the form of radiation is either absorbed or given off.

The energy represents the difference in the orbital energies and so is precisely defined for each possible jump between levels.

Because the energy of a photon is proportional to its frequency, these energy differences will result in radiation with a defined set of frequencies for each element. If the radiation energy emitted from an element is plotted for each frequency in the spectrum, then there will be sharp peaks in the graph at these frequencies.

These are known as emission lines in the spectrum.

On the other hand, if light with a broad range of frequencies passes through a medium containing certain elements or molecules, those elements are found to absorb energy at their characteristic frequencies. The resulting spectrum will be missing those frequencies, and dark lines will appear.

These are known as absorption lines.

As an example, if an element is heated in a star's interior, then it will give off its characteristic radiation which we can detect as bright emission lines on Earth. On the other hand, if broadband light has passed through an absorbing medium between the observer and the light source, then we can determine the elements in that medium by looking for the dark absorption lines.

Free-bound transitions occur when electrons are captured by ions and result in release of energy as recombination occurs. The amount of energy released is dependent on the element formed and the orbit that the electron occupies. As in the bound-bound transition, certain frequencies may dominate.

Free-free radiation occurs when electrons undergo a non-capture collision with an ion or a charged dust particle in the plasma.

The electron's trajectory will be changed as it passes near the other particle, and so it will give off radiation, some of which may be in the visible spectrum.
 

11.6 Radio Radiation in the Cosmos

Radio wavelengths are important because many radio waves can penetrate the Earth's ionosphere and so can be detected by ground-based radio telescopes.

Radio telescope array in New South Wales, Australia. Image credit, University of Waikato and Commonwealth Scientific and Industrial Research Organisation (CSIRO)

Some radio radiation in the cosmos is a result of the collective behavior of large numbers of electrons in a plasma. If the plasma is sufficiently dense, then the electrons can oscillate collectively with a frequency known as the plasma frequency, which depends only on the density of the electrons in the region.

These oscillations generate radiation in the usual way.

This type of radiation often occurs when a beam of electrons, for example, as might be generated by acceleration through a double layer, passes through a region of neutralizing plasma.

There are other radio frequency radiation generating mechanisms where a magnetic field is present. These include cyclotron radiation (where electrons have non-relativistic velocities), Magneto-Bremsstrahlung radiation (where electrons have mildly relativistic velocities), and synchrotron radiation (where electrons have relativistic velocities).

Synchrotron radiation is produced by electrons spiraling along the direction of a magnetic field, such as occurs in Birkeland Currents (image in 11.3 above). The centripetal acceleration causes the radiation. Again, the radiation can occur at all frequencies across the spectrum.

In astrophysics, non-thermal radio emission is, in most cases, synchrotron radiation. This is true for galactic radio emissions, supernovae envelopes, double radio galaxies, and quasars. Additionally, the Sun and Jupiter both produce sporadic synchrotron emissions.

Synchrotron emission can also generate optical frequencies, such as are seen in the Crab Nebula and the M87 'jet'. The Crab Nebula (short YouTube video) also emits quantities of X ray synchrotron radiation.

The analysis of a synchrotron spectrum can give information on the source of the relativistic electrons, which may have a bearing on the origin of cosmic rays, X rays, and Gamma rays in space. Synchrotron radiation is also evidence for the existence of extensive magnetic fields in space and for the conversion, storing, and releasing of large amounts of energy in cosmic plasmas, including galactic jets. More details on synchrotron radiation here for the interested explorer.

Z-pinches can also generate synchrotron radiation as a result of the v × B force.

Radio astronomy can therefore extend the range of information available to us well beyond that derivable from visual telescopes alone.

Detection of higher energy spectra such as X-rays can take this knowledge a stage further.

In all cases we find that plasmas and electric currents within them are excellent emitters of radiation because, as we have seen, electricity in plasma is extremely good at accelerating charged particles, via the electric fields across double layers, which particles then emit the radiation.

This efficient production of radiation by electrical mechanisms seems to be a much more likely source of most of the radiation detected in space than are the huge amounts of Dark Matter and super-dense matter necessary to explain particle acceleration using only gravity.

Of course, 'magnetic reconnection', the alleged breaking and reconnection of magnetic field lines, is also often invoked to explain this type of evidence in the Gravity Model.

As we have seen, this is simply impossible because magnetic field lines don't have a physical existence any more than lines of longitude do.

Back to Contents
 

Summary and Conclusion

Summary

We started by considering the problems that the Gravity Model has in explaining much of the recent evidence of the way the Universe works.

That evidence is coming from ever-better instruments on the ground and in space itself.

We questioned whether it was time to consider a new model of the universe that includes electricity, which is a much stronger force than gravity. The inclusion of electrical principles could explain the evidence without the need to 'invent' another twenty-four times as much matter as we can see.

We have looked at the behavior of electric and magnetic fields and what direct evidence there is for them in space.

We then moved on to consider plasma, the fourth state of matter, whose behavior is well understood from over a hundred years of laboratory experiments and mathematical modeling. We found that plasma is the most widespread form of matter in the Universe. And we found that it is impossible to separate plasma from electricity.

We considered whether we could model plasma behavior by swapping the electrical effects for magnetic ones using Maxwell's equations. But we found that the most interesting types of plasma behavior simply cannot be modeled using magnetic fields alone. We had to consider the effect of charged particles, that is, electricity, instead. We saw the similarity of this problem to the wave-particle duality in particle physics.

We found that a defining characteristic of plasma is to form cells and current-carrying filaments which prefer to align themselves with the magnetic field. We considered the self-sustaining nature of these structures and the way they can transport energy from one region to another, delivering it in forms we can detect here on Earth.

We looked at how the electrical circuits in plasma can develop instabilities and oscillations, and we looked at how electric-motor effects in plasma could cause the rotation we see in galaxies.

And finally we looked at radiation in the visible and other wavelengths. We found that plasma emits vast quantities of radiation, detection of which is the means whereby we obtain most of our evidence of the Universe's behavior.

We have only skimmed the surface of this huge subject, but the glimpses we have seen give us a sense of the power of electricity in plasma.

This power is vastly stronger than the puny force of gravity and, as we have seen, a power which can create many of the effects that we do actually see in the Universe around us.
 

Conclusion

This very brief Guide has attempted to provide an introduction to the behavior of plasma and electricity in space.

Because we live in a thin biosphere on the surface of the Earth, we are not as familiar with these types of behavior of plasma as we are with the behavior of solids, liquids, and gases. Therefore we may not immediately think of plasma behavior when searching for explanations of the universe that we see around us.

Plasma behavior is full of surprises, but once its capabilities are appreciated then it becomes obvious that plasma and electricity together can explain some very complex and powerful phenomena.

These are exactly the sort of phenomena which scientists have been observing since the start of the space age and the invention of telescopes capable of 'seeing' in all the frequencies of the spectrum.

The question is whether these phenomena are more easily explained by electricity and plasma in the Electric Model, or whether it is preferable to keep on adding more and more increasingly improbable patches to the Gravity Model in order to explain each new piece of evidence without using electricity.

In the end, the choice of Model is up to you, the reader. We hope that this Guide has provided enough information to allow you to start making your own decision on this question rather than having to rely solely on what others say.

Back to Contents

Appendix I - Vector Algebra
May 2, 2012

Vector algebra is formulated to handle vectors; i.e., quantities with both magnitude and direction.

Normal algebra, geometry and trigonometry are efficient at dealing with scalar quantities, that is, those with only magnitude, but are inefficient at handling vectors. Vector algebra is an efficient way of solving 2D and 3D problems involving vectors without the need for cumbersome geometry.

The electro-magnetic (e/m) field is a vector field of forces acting on charged objects. As forces are vector quantities (forces acting in an associated direction), the e/m field equations involve vectors.

Vector algebra can be formulated for Cartesian, cylindrical and spherical coordinates.

 Appropriate choice of coordinate system for cylindrically or spherically symmetric problems avoids needless complexity arising from the use of an inappropriate coordinate system and will also clearly show the symmetry of the solution.

Two important results of vector algebra involve multiplication of vectors. Vectors will be indicated by bold text.

The dot product (or "scalar" product) A･B (read as "A dot B") is defined as ||AB|| cos(θ) where A and B are the magnitudes (numeric values) of the vectors A and B respectively and θ is the angle between them. Note that the dot product is a scalar quantity ( a simple numeric value (magnitude) without an associated direction), and geometrically is in a single plane (i.e., 2D).

If the angle between two vectors > 90° then the scalar is negative (<0). If two vectors are perpendicular to one another, their dot product is zero.
 

Examples of dot products at different angles

The cross product A×B (read as "A cross B") is defined as AB sin(θ)an, where an is the unit vector normal to the plane of A and B.

Note that the cross product of two vectors is also a vector and its direction is orthogonal (perpendicular) to both A and B; i.e., the resultant vector involves a third dimension compared to the 2D plane containing the first two vectors.

Vector algebra defines another important operator, Del, or Δ. Del is analogous to the differential operator D in calculus where D represents the operation d/dx. Two further results using Del are important in analyzing e/m fields.

Δ･A or Div A is the divergence of the vector field A. The divergence is a scalar and is similar to the derivative of a function. If the divergence of a region of a vector field is non-zero then that region is said to contain sources (Div A>0) or sinks (Div A<0) of the field.

For example, an arbitrary closed surface around an isolated positive charge in a static electric field contains the source of the electric flux, that is the positive point charge; therefore the divergence of the electric flux density vector field over that surface will be positive, and equal to the enclosed charge. This is Gauss' Law. (see Appendix II, e/m field equations)

Note that Div A involves a dot product and is therefore dependent on angles. The angle is usually that between the vector and the normal to the surface being analyzed.

Δ×A or Curl A is the curl of the vector field A.

The curl of a vector field is another vector field which describes the rotation of the first vector field; the magnitude of Δ×A is the magnitude of the rotation, and the direction of Δ×A is the axis of that rotation as determined by the right-hand rule. If one imagines any 3D vector field to represent fluid flow velocities, then the curl of the field at a point would be indicated by the way a small sphere or a paddlewheel placed at that point would be rotated by the flow.

In a 2D flow it is easy to see that the direction of the axis of rotation of a circle (the 2d analogue of a sphere) in the flow will be in the third dimension, as is given by the use of the cross product in calculating the curl.

Additionally, the Del operator can be applied to a scalar field V. ΔV or Grad V is a vector field defining the gradient of the scalar function V.

ΔV lies in the direction of the maximum increase of the function V. If applied to a potential function, then Grad V is a vector field that is everywhere normal to the equipotential surfaces.

Two useful properties of the Curl operator are:

(1) the divergence of the curl of any vector field is the zero scalar; i.e., Δ･(Δ×A) = 0

(2) the curl of a gradient of any vector field is the zero vector; i.e. Δ×(Δf) = 0 for any scalar function f dependent on position, as in f(x,y,z)

Example:

To visualize (2), think of a scalar field such as an area of hilly land, where contours of constant elevation above sea level are "drawn" along the ground.

 

Elevation "h" at any given point (x,y,z) would then vary with position, so its function is h(x,y,z). The gradient del(h) would be a vector that points, starting at the point (x,y,z), perpendicular to the contour line through (x,y,z) and straight "down the hill".

Imagine the way water flows downhill, or which way a marble would roll, and that's the direction the gradient vectors point, always perpendicular to the equal-elevation contour at any point.

Because these vectors are straight, they have no curl, or bend.

That's why, mathematically, 'del × (del h) = 0′.

In practice, this means that an electric field in which the lines of flux are straight (e.g., between the layers of a plasma double layer or a capacitor, ignoring edge effects where the lines are not straight), a charged particle will be accelerated from rest in a straight line: the electric field has no curl.

Vector algebra becomes even more important in analyzing particle interactions when several forces may be present, as when a charged particle enters both an electric field and an associated magnetic field simultaneously, at an oblique angle so that its motion vector can have one component normal to the field lines and another ("drift") parallel to them.

The Mathematica©-based images in Chapter 4, ¶4.3, are indicative of some of the complexities of such interactions using only 1 particle.

Plasma are double digit orders of number of particles higher than this simplest case, and the feedback mechanisms and complex particle motions that develop cause the plasma to create and maintain charge separation, to separate bodies with one electrical field potential from a volume of different potential, to initiate current flows, to accelerate particles to relativistic velocities and radiate strongly, to pinch and roll up current sheets into filamentary conducting plasma structures like lightning, coronal loops and galactic jets.
 

Back to Contents

Appendix II - The Electro-magnetic Field Equations
June 20, 2012

Introduction

Maxwell's Equations and the Lorentz Force Law together comprise the e/m field equations; i.e., those equations determining the interactions of charged particles in the vicinity of electric and magnetic fields and the resultant effect of those interactions on the values of the e/m field.

For ease of explanation, the following will refer to "fields" as though they possess some independent physical reality. They do not.

The use of fields is as an aid in understanding how forces exerted by and upon real particles, and how the positions (coordinates) of those particles may exist at a given time, or may vary over an interval of time.

Field lines are also convenient notational devices to aid in understanding what physically is going on, and are not "real". An oft-used example is the set of lines or contours of equal elevation relative to some fixed reference value, often found on topographic maps of land areas, and varying pressure distributions on weather charts.

Such lines do not exist as real physical entities; they can be used for calculation and visualization of simple or complex phenomena, but they do not effect changes or position or exert force or anything else, themselves.

Imagining that they are real is called reification; it can be a convenient aid to better understanding, but it is incorrect to say that field lines of any type are real or "do" anything.

The implications of Maxwell's Equations and the underlying research are:

• A static electric field can exist in the absence of a magnetic field; e.g., a capacitor with a static charge Q has an electric field without a magnetic field.

• A constant magnetic field can exist without an electric field; e.g., a conductor with constant current I has a magnetic field without an electric field.

• Where electric fields are time-variable, a non-zero magnetic field must exist.

• Where magnetic fields are time-variable, a non-zero electric field must exist.

• Magnetic fields can be generated in two ways other than by permanent magnets: by an electric current, or by a changing electric field.

• Magnetic monopoles cannot exist; all lines of magnetic flux are closed loops.

The Lorentz Force Law

The Lorentz Force Law expresses the total force on a charged particle exposed to both electric and magnetic fields. The resultant force dictates the motion of the charged particle by Newtonian mechanics.

F = Q(E + U×B) (remember, vectors are given in bold text)

...where F is the Lorentz force on the particle; Q is the charge on the particle; E is the electric field intensity (and direction); and B is the magnetic flux density and direction.

Note that the force due to the electric field is constant and in the direction of E, so will cause constant acceleration in the direction of E. However, the force due to the combination of the particle's velocity and the magnetic field is orthogonal to the plane of U and B due to the cross product of the two vectors in vector algebra (Appendix I).

The magnetic field will therefore cause the particle to move in a circle (to gyrate) in a plane perpendicular to the magnetic field.

If B and E are parallel (as in a field-aligned current situation) then a charged particle approaching radially toward the direction of the fields will be constrained to move in a helical path aligned with the direction of the fields; that is to say, the particle will spiral around the magnetic field lines as a result of the Lorentz force, accelerating in the direction of the E field.
 

Further Discussion of Maxwell's Equations

The Maxwell Equations are the result of combining the experimental results of various electric pioneers into a consistent mathematical formulation, whose names the individual equations still retain.

They are expressed in terms of vector algebra and may appear, with equal validity, in either the point (differential) form or the integral form.

The Maxwell Equations can be expressed as a General Set, applicable to all situations; and as a "Free Space" set, a special case applicable only where there are no charges and no conduction currents.

The General Set is the one which applies to plasma:

where

• E is the electric field intensity vector in newtons/coulomb (N/C) or volts/meter (V/m)

• D is the electric flux density in C/m2; D = εE for an isotropic medium of permittivity ε

• H is the magnetic field strength and direction in amperes/meter (A/m)

• B is the magnetic flux density in A/N･m, or tesla (T); B = μH for an isotropic medium of permeability μ

• Jc is the conduction current density in A/m2; Jc = σE for a medium of conductivity σ

• ρ is the charge density, C/m³

Gauss' Law states that "the total electric flux (in coulombs/m2) out of a closed surface is equal to the net charge enclosed within the surface".

By definition, electric flux ψ originates on a positive charge and terminates on a negative charge. In the absence of a negative charge flux "terminates at infinity". If more flux flows out of a region than flows into it, then the region must contain a source of flux; i.e., a net positive charge.

Gauss' Law equates the total (net) flux flowing out through the closed surface of a 3D region (i.e., a surface which fully encases the region) to the net positive charge within the volume enclosed by the surface. A net flow into a closed surface indicates a net negative charge within it.

Note that it does not matter what size the enclosing surface is - the total flux will be the same if the enclosed charge is the same.

A given quantity of flux emanates from a unit of charge and will terminate at infinity in the absence of a negative charge. In the case of an isolated single positive charge, any sphere, for example, drawn around the charge will receive the same total amount of flux. The flux density D will reduce in proportion (decrease per unit area) as the area of the sphere increases.

Gauss' Law for Magnetism states that "the total magnetic flux out of a closed surface is zero".

Unlike electric flux which originates and terminates on charges, the lines of magnetic flux are closed curves with no starting point or termination point. This is a consequence of the definition of magnetic field strength, H, as resulting from a current (see Ampere's Law, below), and the definition of the force field associated with H as the magnetic flux density B = μH in teslas (T) or newtons per amp meter (N/Am).

Therefore all magnetic flux lines entering a region via a closed surface must leave the region elsewhere on the same surface. A region cannot have any sources or sinks.

This is equivalent to stating that magnetic monopoles do not exist.
 

Ampere's Law with Maxwell's Correction

Ampere's Law is based on the Biot-Savart Law,

dH = (I dl×ar) / 4πR2

...which states that "a differential (i.e., tiny segment of) magnetic field strength dH at any point results from a differential current element I dl of a closed current path of current I).

The magnetic field strength varies inversely with the square of the distance R from the current element and has a direction given by the cross-product of I dl and the unit vector ar of the line joining the current element to the point in question.

The magnetic field strength is also independent of the medium in which it is measured.

As current elements have no independent existence, all elements making up the complete current path, i.e., a closed path, must be summed to find the total value of the magnetic field strength at any point.

Thus:

H = ∫ (I dl×ar) / 4πR2

...where the integral is a closed line integral which may close at infinity.

Thence, for example, an infinitely long straight filamentary current I (closing at infinity) will produce a concentric cylindrical magnetic field circling the current in accordance with the right-hand rule, with strength decreasing with the radial distance r from the wire, or:

H = (I/2πr) ar

(note the vector notation in cylindrical coordinates; the direction of H is everywhere tangential to the circle of radius r)

Ampere's Law effectively inverts the Biot-Savart Law and states that "the line integral of the tangential component of the magnetic field strength around a closed path is equal to the current enclosed by the path", or,

∫H・dl = Ienc where the integral is a closed line integral

Alternatively, by definition of curl, Curl H or Δ×H = J, the current density.

This effectively means that a magnetic field will be generated by an electric current.

However, this only applies to time-invariant currents and static magnetic fields. As Jc = σE, this implies that the electric field is constant as well.

To overcome these restraints so as to allow for time-varying charge density and to allow for the correct interpretation of the propagation of e/m waves, Maxwell introduced a second term based on the Displacement Current, JD, where,

JD = δD/δt

...arising from the rate of change of the electric field E.

Maxwell's correction, as included in the revised Law, dictates that a magnetic field will also arise due to a changing electric field.

Faraday's Law states that "if the magnetic flux Φ, linking (i.e., looping through) an open surface S bounded by a closed curve C, varies with time then a voltage v around C exists"; specifically,

v = -dΦ/dt

...or, in integral form,

∫cE･dl = -d(∫s B･dS)/dt for a plane area S and B normal to S

Thus if B varies with time there must be a non-zero E present, or, a changing magnetic field generates an electric field.

The minus sign in the equation above indicates Lenz's Law, namely "the voltage induced by a changing flux has a polarity such that the current established in a closed path gives rise to a flux which opposes the change in flux".

In the special case of a conductor moving through a time-invariant magnetic field, the induced polarity is such that the conductor experiences magnetic forces which oppose its motion.

Back to Contents

Appendix III - The Electromagnetic Field Equations
 

III. A. Summary
 

Maxwell's Equations and the Lorentz Force Law together comprise the EM field equations, that is, those equations determining the interactions of charged particles in the vicinity of electric and magnetic fields and the resultant effect of those interactions on the values of the EM field.

For ease of explanation, the following will refer to 'fields' as though they possessed some independent physical reality. However, see Appendix I: The Nature of Electro-magnetic Fields for the dangers inherent in such reification.

The implications of Maxwell's Equations and the underlying research are:

• A static electric field can exist in the absence of a magnetic field, for example, a capacitor with a static charge Q has an electric field without a magnetic field.

• A constant magnetic field can exist without an electric field, for example, a conductor with constant current I has a magnetic field without an electric field.

• Where electric fields are time-variable, a nonzero magnetic field must exist.

• Where magnetic fields are time-variable, a nonzero electric field must exist.

• Magnetic fields can be generated in two ways other than by permanent magnets: by an electric current or by a changing electric field.

• Magnetic monopoles cannot exist; all lines of magnetic flux are closed loops.

III. B. The Lorentz Force Law

The Lorentz Force Law expresses the total force on a charged particle exposed to both electric and magnetic fields. The resultant force dictates the motion of the charged particle by Newtonian mechanics.

F = Q(E + U x B) (Vectors are given in bold text)

...where F is the Lorentz force on the particle, Q is the charge on the particle, E is the electric field intensity, U is the velocity of the particle, and B is the magnetic flux density.

Note that the force due to the electric field is constant and in the direction of E, so it will cause constant acceleration in the direction of E. However, the force due to the combination of the particle's velocity and the magnetic field is orthogonal to the plane of U and B due to the cross product of the two vectors in vector algebra. The magnetic field will therefore cause the particle to move in a circle in a plane perpendicular to the direction of the magnetic field.

If B and E are parallel (as in a field-aligned current situation), then a charged particle approaching radially towards the direction of the fields will be constrained to move in a helical path aligned with the direction of the fields.

That is to say, the particle will spiral around the magnetic field lines as a result of the Lorentz force, accelerating in the direction of the E field.

 

III. C. Further Discussion of Maxwell's Equations

C.1

The Maxwell Equations are the result of combining the experimental results of various electrical pioneers into a consistent mathematical formulation, whose names the individual equations still retain.

 

They are expressed in terms of vector algebra and may appear, with equal validity, in either the point (differential) form or the integral form.

The Maxwell Equations can be expressed as a General Set, applicable to all situations, and as a 'Free Space' Set, a 'special case' applicable only where there are no charges and no conduction currents. Clearly, the General Set is the one which applies to plasma.

 

Maxwell's Equations - General Set
 

...where,

E is the Electric field intensity in Newtons/Coulomb (N/C) or Volts/metre (V/m)

D is the electric flux density in C/m2; D = εE for an isotropic medium of permittivity ε

H is the magnetic field strength in Amps/metre (A/m)

B is the magnetic flux density in N/A.m; B = μH for an isotropic medium of permittivity μ

Jc is the conduction current density in A/m2; Jc = σE for a medium of conductivity σ

ρ is the charge density

C.2

Gauss' Law states that the total electric flux (in Coulombs / m2 ) out of a closed surface is equal to the net charge enclosed within the surface.

By definition, electric flux Ψ originates on a positive charge and terminates on a negative charge. In the absence of a negative charge, the flux terminates at infinity. If more flux flows out of a region than flows into it, then the region must contain a source of flux, that is, a net positive charge.

Gauss' Law equates the total (net) flux flowing out through the closed surface of a 3D region (that is, a surface which fully encases the region) to the net positive charge within the volume enclosed by the surface. A net flow into a closed surface indicates a net negative charge within it.

The vector dot product ensures that only the normal component of the flux relative to the surface at any point is counted towards the total flux. The tangential component is not leaving the region and therefore is not counted.

Note that it does not matter what size the surface is; the total flux will be the same if the enclosed charge is the same. A given quantity of flux emanates from a unit of charge and will terminate at infinity in the absence of a unit of negative charge.

 

In the case of an isolated single positive charge, any sphere, for example, drawn around the charge will receive the same total amount of flux, and the flux density D will reduce in proportion as the area of the sphere increases.

 

 

C.3

Gauss' Law for Magnetism states that the total magnetic flux out of a closed surface is zero.

Unlike electric flux, which originates and terminates on charges, the lines of magnetic flux are closed curves with no starting point or termination point.

 

This is a consequence of the definition of magnetic field strength, H, as resulting from a current (see Ampere's Law below), and the definition of the force field associated with H as the magnetic flux density B = μH in Teslas or Newtons per Amp metre (N/Am)

Therefore all magnetic flux lines entering a region via a closed surface must leave the region elsewhere on the same surface. A region cannot have any sources or sinks.

 

This is equivalent to stating that magnetic monopoles do not exist.

III. D. Ampere's Law with Maxwell's Correction

D.1

Ampere's Law is based on the Biot-Savart Law:

dH = (I dl x ar ) ÷ (4πR2)

...which states that a differential (that is, segment) of magnetic field strength dH at any point results from a differential current element I dl (that is, a segment of length dl of a closed current path of current I).

 

The magnetic field strength varies inversely with the square of the distance R from the current element and has a direction given by the cross product of I dl and the unit vector ar of the line joining the current element to the point in question. The magnetic field strength is also independent of the medium in which it is measured.

As current elements have no independent existence, all elements making up the complete current path, that is, a closed path, must be summed to find the total value of the magnetic field strength at any point.

 

Thus:

H = ∫(I dl x ar ) ÷ (4πR2)

...where the integral is a closed line integral which may close at infinity.

Thence, for example, an infinitely long straight filamentary current I (closing at infinity) will produce a concentric cylindrical magnetic field circling the current in accordance with the right-hand rule, with strength decreasing with the radial distance r from the wire, or,

H = (I / (2πr) aΦ

(note the vector notation in cylindrical coordinates: the direction of H is everywhere tangential to the circle of radius r)
 

D.2

Ampere's Law effectively inverts the Biot-Savart Law and states that the line integral of the tangential component of the magnetic field strength around a closed path is equal to the current enclosed by the path, or,

∫H⋅dl = Ienc

...where the integral is a closed line integral.

Alternatively, by the definition of curl, Curl H or Δ x H = J, the current density.

This effectively means that a magnetic field will be generated by an electric current. However, this only applies to time-invariant currents and static magnetic fields. As Jc = σE, this implies that the electric field is constant as well.

To overcome these restraints so as to allow for time-varying charge density and to allow for the correct interpretation of the propagation of e/m waves, Maxwell introduced a second term based on the Displacement Current, JD where,

JD = δD/δt

...arising from the rate of change of the electric field E.

Maxwell's correction, as included in the revised Law, dictates that a magnetic field will also arise due to a changing electric field.
 

D.3

Faraday's Law states that 'if the magnetic flux φ linking (i.e. looping through) an open surface S bounded by a closed curve C varies with time then a voltage v around C exists'; specifically,

v = - dφ/dt

or, in integral form,

∫c E⋅dl = - d(∫sB⋅dS) / dt for a plane area S and B normal to S

Thus if B varies with time there must be a non-zero E present; i.e. a changing magnetic field generates an electric field.

The minus sign in the equation above indicates Lenz's Law, namely 'the voltage induced by a changing flux has a polarity such that the current established in a closed path gives rise to a flux which opposes the change in flux'.

In the special case of a conductor moving through a time-invariant magnetic field, the induced polarity is such that the conductor experiences magnetic forces which oppose its motion.

Back to Contents