|

|
Miraculously, the original Head-Hand-Foot circles - which I had first fitted
to the image by eye, and without consideration for any plan other than form
itself - fall into the kind of position with the Monkey Star (the X-Star 3),
which is easily and completely described in general geometrical terms. This
means that we can reproduce the circles to scale in the position of any
given 5-pointed star.
This reconstruction above involves a number of alignments either parallel,
or perpendicular to the Big X's line 'b on the left above. |
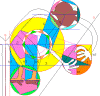 |
Hand-circle's Exact Coordinates
The monkey's hands invoke the inner X-Star circle with admirable accuracy.
First coordinate for the Hand Circle:
The Hand-circle centers right on (+/- 3mm) the vertical line b1 emanating
from the star's tip just above. Hence line b1 is a major line in the Monkey
Star's grid.
|
Second coordinate for the Hand Circle.
Pentagon No. 2 in the diagram above is a direct projection of the inner
pentagon of the Monkey Star. When it rotates about the Monkey Star's center,
its tip describes a circle (in yellow above), which is tangent to the
Hand-circle (see below). This solves the second coordinate for the
Hand-circle.
At this point, we can reconstruct the Hand-circle, and the line-1, which is
the laser-like line of sight from the center of the Monkey Star through a
pointlike aperture between the hands. We can also reconstruct line 3.
|
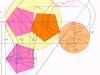 |
Foot-circle's Exact Coordinates
First coordinate of the Foot Circle:
When we inscribe a pentagon into the Foot-Circle, its vertical side (b5)
passes through the center of the Monkey-Star (X-Star 3).
In the diagram above, the vertical side of the (purple) pentagon No.2
originates from the center of the X-Star. It shares all its verticals with
the Foot-Circle's pentagon, as if the Foot Circle's pentagon was its
projection directly downwards.
With 'b' vertical, it is as if the monkey were standing up.
Second coordinate of the Foot-circle:
This idea is straightforward. The Line-3 originates at the same point, at
which the Line-1 exits the Hand-circle. It is vertical to 'b', and also a
tangent to the top of the Foot-circle. This line gives the Foot-circle's
elevation. Now, we may reconstruct the Foot circle, as well.
Special Effect
Two distances involved measure 17.9999.. X-Star meters - almost a perfectly
round value: These are the distances of the centers of both the Foot-circle
and the Monkey Star to the nearest corner of the other circle's pentagon.
The Head-circle
First coordinate of the Head Circle
A line through the Head Circle's center perpendicular to the line-1 is a
tangent to the inner X-Star circle. And the line drawn from the center of
the X-Star as a tangent to the Head Circle will be perpendicular to the
line-1. This yields one coordinate.
The second coordinate for the Head-circle
It is given by the Main Square, not seen in the diagram above. It involves
a major line of the square's grid through the 1/4 point of its diagonal 'y'.
The distance between the centers of the Head-circle and the Cone's
Key-circle is quite
interesting
11.777,777,67... X-Star meters.
Truly, the monkey performs so many fine balances and alignments, a most
adroit android could not easily duplicate them all! I wonder, could an
android, or a robot make good use of a long tail?
A smiley is mandatory here, but the question is as good as any.
|

