|

24 Agosto 2017
del Sitio Web
AgenciaSINC

La tablilla babilónica Plimpton 322
presenta cuatro columnas (separadas por tres hendiduras)
y 15
filas de números cuneiformes,
pero
seguramente tuvo más porque está fragmentada.
UNSW/Andrew
Kelly
El
arqueólogo que inspiró el personaje de Indiana
Jones, el estadounidense Edgar Banks, descubrió hace
un siglo en Irak una enigmática tablilla babilónica
repleta de números cuneiformes.
Tras un siglo
de debates matemáticos, investigadores australianos
desvelan ahora su secreto:
se trata de
una tabla trigonométrica de hace 3800 años, la
más antigua conocida hasta la fecha, que enseña
como hacer cálculos trigonométricos sin ángulos
y con una precisión sin precedentes.
Dos investigadores (Daniel Mansfield y Norman Wildberger)
de la Universidad de Nueva Gales del Sur (UNSW, Australia) han
analizado una famosa tablilla de arcilla babilónica, datada entre
entre 1822 y 1762 AC, y han descubierto que se trata de la tabla
trigonométrica más antigua y precisa del mundo.
Posiblemente los antiguos
escribas matemáticos las utilizaban para realizar los cálculos
necesarios para levantar templos, palacios, canales y otras
construcciones.
La tablilla confirma
que 'los babilonios' se
adelantaron
en más de mil años a los
griegos
en la 'invención' de la
trigonometría
El estudio (Plimpton
322 is Babylonian Exact Sexagesimal Trigonometry)
confirma que 'los babilonios' se adelantaron en más de mil años a
los griegos en la 'invención' de la trigonometría (el estudio de los
triángulos) y muestra un sofisticado y antiguo conocimiento
matemático que había permanecido oculto hasta ahora.
La tablilla, denominada
Plimpton 322, fue descubierta en la
primera década del siglo XX, en lo que ahora es el sur de Irak, por
el diplomático, arqueólogo, académico y comerciante de antigüedades
Edgar J. Banks, el personaje
real en el que se basó otro de ficción mucho más popular: Indiana
Jones...

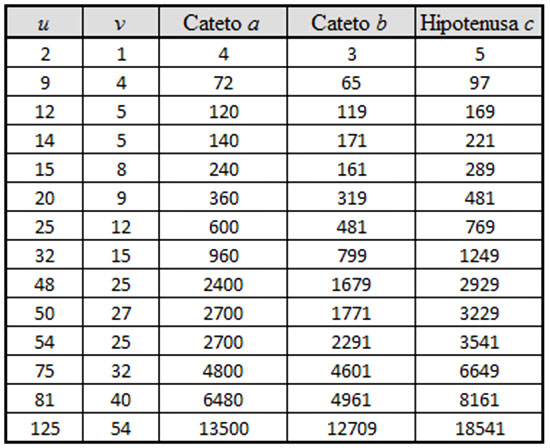
En esta tablilla aparecen grabadas, con la escritura cuneiforme de
la época, una serie de cuatro columnas y 15 filas de números que
siguen un original sistema sexagesimal (de base 60, como nuestro
sistema horario), en lugar del sistema decimal con base 10 que
utilizamos hoy en día.
Las cifras describen una
secuencia de 15 triángulos rectángulos, que van reduciendo su
inclinación y 'aplanando' fila tras fila.
Basándose en estudios previos y observando que el borde izquierdo de
la arcilla está roto, los investigadores plantean que Plimpton 322
tuvo originalmente seis columnas y probablemente debía estar formada
por 38 filas de caracteres cuneiformes.
Ternas
pitagóricas mucho antes de Pitágoras
"Esta tablilla lleva
desconcertado a los matemáticos desde hace más de 70 años,
porque se dieron cuenta de que contiene un patrón especial de
números llamado terna pitagórica", explica uno de los autores,
Daniel Mansfield, de la Escuela de Matemáticas y Estadística de
la UNSW en Sidney.
Una
terna pitagórica es una lista de
tres números enteros positivos:
a, b y c, donde se
cumple que a2 + b2 = c2.
Un ejemplo sencillo son
los números enteros 3, 4 y 5, pero los valores que presenta Plimpton
322 a menudo son considerablemente mayores, como los que refleja en
su primera fila, donde aparece el triplete 119, 120 y 169.
El nombre de esta terna se deriva del teorema de Pitágoras,
que para un triángulo rectángulo establece que el cuadrado de la
hipotenusa (lado opuesto al ángulo recto) es la suma de los
cuadrados de los otros dos lados.
"Los babilonios
conocían los triples pitagóricos mucho antes de que naciera
Pitágoras, como se puede ver en esta y otras tablillas", señala
Mansfield a SINC.
"Además nos enseñan
cómo hacer trigonometría sin usar los ángulos, una trigonometría
mucho más simple que no requiere conceptos avanzados como
ángulos o números irracionales".
Los 'babilonios' enseñan
cómo hacer una trigonometría
sin ángulos
y posiblemente la usaban para
levantar sus construcciones,
según los investigadores
La desconocida
trigonometría que describe la tablilla para los triángulos
rectángulos se basa en ratios o relaciones, no en ángulos ni
círculos.
Según los autores, es una
obra matemática fascinante que demuestra el genio de sus creadores:
"La tablilla no sólo
contiene la tabla trigonométrica más antigua del mundo, sino que
también es la única completamente precisa, debido al diferente
enfoque babilónico de la aritmética y la geometría".

El estudio, que se
publica en
Historia Mathematica (la
revista oficial de la Comisión Internacional de Historia de las
Matemáticas), apunta la predilección de los babilonios por la
precisión de los números, y compara la tablilla con la llamada
tabla de senos de Madhava
(construida en el siglo XIV por este matemático y astrónomo indio),
demostrando que Plimpton 322 es una tabla trigonométrica "exacta y
potente".
Las tablas trigonométricas permiten usar la información de un lado
de un triángulo rectángulo para determinar la de los otros dos.
Hasta ahora se
consideraba al astrónomo griego
Hiparco, que vivió alrededor de
120 AC, como el padre de la trigonometría, y a su 'tabla
de cuerdas' como la tabla trigonométrica más antigua.
"Pero Plimpton 322
precede a Hiparco en más de 1000 años", insiste el otro autor,
el profesor Norman Wildberger, quien considera que gracias a
esta tablilla se abren nuevas posibilidades no sólo para la
investigación matemática moderna, sino también para la educación
matemática.
"Nos ofrece una
trigonometría más simple, más precisa, que tiene claras ventajas
sobre la nuestra".
El mundo antiguo
enseñando algo nuevo
"Esto significa que
tiene gran relevancia para nuestro mundo moderno", añade
Mansfield por su parte.
"La matemática
babilónica puede no haber estado de moda durante más de 3000
años, pero hoy tiene posibles aplicaciones prácticas en
topografía, gráficos por ordenador y en el campo de la
educación.
Es un raro ejemplo
del mundo antiguo enseñándonos algo nuevo".

"Plimpton 322 era una herramienta poderosa que podría haber sido
utilizada en la topografía de los campos o para los cálculos
arquitectónicos en la construcción de palacios, templos o
pirámides escalonadas", aventura Mansfield.
Reconoce a SINC que, en
realidad,
"es difícil decirlo
con seguridad, porque nuestra ventana a ese mundo es muy
pequeña: sólo podemos echar un vistazo y decir lo que parece
ser".
La matemática 'babilónica'
puede no haber estado de moda
durante más de 3000 años,
pero hoy todavía se puede
aplicar,
dicen los autores
En cualquier caso, los
autores descartan que, como se pensaba hasta ahora, la tablilla
sirviera simplemente para que los profesores de la época comprobarán
las soluciones de los estudiantes a la hora de resolver problemas de
ecuaciones cuadráticas.

Plimpton 322, que se cree procede de la antigua
ciudad sumeria de Larsa (a unos 250
Km. al sur de Bagdad), actualmente se conserva en la Biblioteca
de Manuscritos y Libros Raros de la Universidad de Columbia en
Nueva York.
"Existe un tesoro de
tablillas 'babilónicas' como esta, pero sólo se ha estudiado una
parte.
El mundo matemático
está empezando a descubrir que la antigua, aunque muy
sofisticada, cultura matemática de los babilonios todavía tiene
mucho que enseñarnos", concluye Wildberger.
Video
|