|
|
|
by David Wilcock 2002 from NoNeedToKnow Website
ATLANTEAN SECRETS REVISITED
Then, roughly 12,000 years ago, a worldwide cataclysm
caused the destruction of both civilizations. As the years passed, those who
inherited the scientific knowledge would have more and more difficulty
seeing “the big picture.”
Some of these visualizations took the form of studying mandalas, such as the Sri Yantra formation.
Others preferred to engage in dances where the movements and music were in tune with these geometric patterns. Still others preferred to assemble, sculpt and / or draw these forms with a compass and straightedge, hence the importance of the main symbol of the Masonic fraternity, which has the letter “G”, symbolizing “God,” “Geometry” and the “Great Architect of the Universe,” surrounded by a compass above it and a straightedge below it.
Pre-Masonic groups such as the
Knight Templars chose to encode these geometric relationships into their
sacred structures, such as the stained-glass windows in cathedrals.
SACRED GEOMETRY AND THE PLATONIC SOLIDS
We have written extensively on this subject in both of our previous books, and the reader is encouraged to refer back to them for greater understanding. In short, sacred geometry is simply another form of vibration, or “crystallized music.”
Consider the following example:
In two dimensions, we can either use an oscilloscope or vibrate a flat circular “Chladni plate” and see nodes develop that will form common geometric forms such as the square, triangle and hexagon when connected together.
This work has been repeated many times by Dr. Hans Jenny, Gerald Hawkins and others.
Though this is a very simple concept in terms of wave mechanics, Gerald Hawkins was the first to establish mathematically that such geometries inscribed within circles were indeed musical relationships.
We may be surprised to realize that he was led to this discovery by analyzing various geometric crop formations that would appear overnight in the fields of the British countryside.
This has been covered in both of our previous volumes.
Here, the tetrahedron is shown as a “star tetrahedron” or interlaced tetrahedron, meaning that you have two tetrahedra that are joined together in perfect symmetry:
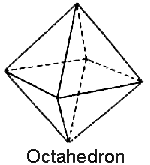
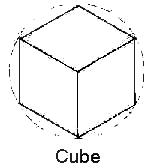
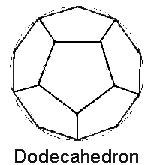
Figure 3.1 – The five basic Platonic Solids.
Here are some of the main rules for these geometric solids:
And most importantly,
Similar to the two-dimensional cases involving the triangle, square, pentagon and hexagon inside the circle, the Platonic Solids are simply representations of waveforms in three dimensions.
This point cannot be
stressed strongly enough. Each tip or vertex of the Platonic Solids touches
the surface of a sphere in an area where the vibrations have canceled out to
form a node. Thus, what we are seeing is a three-dimensional geometric image
of vibration / pulsation.
A small number of evenly-distanced nodes would form across the surface of the sphere, as well as thin lines that connected them to each other. If you have four evenly spaced nodes, you will see a tetrahedron. Six evenly spaced nodes form an octahedron. Eight evenly spaced nodes form a cube. Twenty evenly spaced nodes form the dodecahedron, and twelve evenly spaced nodes form the icosahedron.
The straight lines that we see on these geometric objects simply represent the stresses that are created by the “closest distance between two points” for each of the nodes as they distribute themselves across the entire surface of the sphere.
Figure 3.2 – Dr. Hans Jenny’s Platonic Solid formation in spherical vibrating fluid.
Dr. Hans Jenny conducted a similar experiment, a small part of which is pictured here in Figure 3.2, wherein a droplet of water contained a very fine suspension of light-colored particles, known as a “colloidal suspension.”
When this roughly spherical droplet of particle-filled water was vibrated at various “Diatonic” musical frequencies, the Platonic Solids would appear inside, surrounded by elliptical curving lines that would connect their nodes together, as we see in the picture, where it is clear that there are two tetrahedrons in the central area.
If the droplet were a
perfect sphere instead of a flattened sphere, then the formations would be
even more clearly visible.
PLATONIC SOLIDS AND “SYMMETRY” IN PHYSICS
For this reason, they
are often seen in theories that deal with multi-dimensionality, where many
“planes” need to intersect in symmetrical ways so that they can be rotated
in a number of ways and always remain in the same positions relative to each
other. These multi-dimensional theories include “group theory,” also known
as “gauge theory,” which consistently features various Platonic models for
“infolded” hyperdimensional space.
When we keep in mind the symmetrical quality of the Solids as we have indicated, Dr. Wolff’s words from Chapter 5 entitled On the Importance of Living in Three Dimensions should make good sense to us:
The Platonic Solids have the greatest geometric symmetry of any shapes in existence, though Dr. Wolff does not call them by name here.
In the next excerpt from Dr. Aspden, he refers to the Platonic Solid forms in the aether as “fluid crystals,” and explains how they can have an effect similar to a solid, even while they are appearing in a fluidlike medium:
This gives us a “solid” explanation for why Tesla said that the
aether
“behaves as a liquid for matter, and as a solid for light and heat". The
Platonic Solids actually do act as if they were structural frameworks within
the aether, organizing the energy flows into specific patterns.
Torsion waves
have been seen to follow the “phi” pattern as well, which shall be more
fully explored when we discuss the under-appreciated “pyramid power”
phenomenon and the “cavity structural effect” pioneered by Dr. Victor Grebennikov in Chapter Seven.
MICROCLUSTER PHYSICS
Microclusters are tiny “particles” that present clear and straightforward evidence that atoms are vortexes in the aether that naturally assemble into Platonic Solid formations by their vibration / pulsation. Furthermore, these new discoveries pose quite a challenge for those who still believe that there must be single electrons orbiting a nucleus instead of standing-wave electron clouds of aetheric energy that assemble into geometric patterns.
The story of “microclusters” first broke into the mainstream world in the December 1989 issue of Scientific American, in an article by Michael A. Duncan and Dennis H. Rouvray:
Less than two years after this story broke in the mainstream, the science of microcluster physics was realized in its own graduate-school textbook authored by Satoru Sugano and Hiroyasu Koizumi. Microcluster Physics was published by the respectable, mainstream Springer-Verlag corporation as volume 21 in a series of texts in the field of materials science.
All of the quotes from this text that we shall use are from its revised second edition, which was released in 1998.
In Sugano and Koizumi’s text, we are told that with the new discoveries of microclusters, we can now arrange groupings of atoms into four basic categories of size, each with different properties:
When we study the above list, we would initially expect that microclusters would have traits in common with molecules and with fine particles both, but in fact they have properties that neither display, as Sugano et al. explain here:
As we continue reading, we learn that microclusters do not form randomly from any group of 10-1000 atoms; only certain “magic numbers” of atoms will gather together to form microclusters.
The next quote describes how this was first discovered, and when we read it we should remember that the “mass spectrum” being mentioned describes spectroscope analysis, which we covered in the last chapter.
When “cluster beams” are being discussed, this means that atoms (such as Na, or sodium) are being blasted through a tiny nozzle to form into a “beam” that is then analyzed.
Most importantly, as the atoms blast out of the nozzle, some of them spontaneously gather into microclusters, which demonstrate anomalous properties:
Our next quote comes from the first area in Sugano and Koizumi’s book where specific details are given regarding the highly anomalous physical properties of microclusters.
Though they are only slightly smaller than fine particles in terms of the number of atoms, they are much more stable. Here, the greater stability refers to the fact that microclusters burn at a much higher temperature than molecules or fine particles of the same elements.
According to David Hudson, (whom we shall discuss later,) Russian scientists were the first to discover that microclusters must be burned for more than 200 seconds to reveal a color spectrum to be analyzed, whereas all other known molecular compounds burn up in a maximum of about 70 seconds:
The “nearly spherical” shapes that are described above will be seen in later quotes as the Platonic Solids and related geometries.
Our next passage is probably too technical for most readers and can be skipped over, but it is a clear-cut description of how the “cluster beams” are being made and analyzed and what specific “magic numbers” of atoms emerged.
Furthermore, we should note that the clusters that are formed become electrically neutral, which is another anomalous and unexpected result:
Now pay very close attention to the next sentence, as its significance can easily be missed:
What this is telling us is that the hypothetical “electrons” are no longer bound to their individual atoms in microclusters, but rather move independently throughout the entire cluster itself!
Remember that in our new quantum model, there are no electrons, only clouds of aetheric energy that are flowing in towards the nucleus via the Biefield-Brown effect. In this case, the microcluster acts as one single atom, with the center of the cluster becoming akin to the positively-charged atomic nucleus where the negatively-charged energy is flowing in.
Interestingly, in keeping with the fluidlike behaviors of the aether, the next passage suggests that the microclusters can have properties similar to a fluid as well as a solid:
The next excerpt comes from a completely different study by Besley et al., referenced at the end of this chapter, entitled Theoretical Study of the Structures and Stabilities of Iron Clusters.
Obviously, their work builds directly off of Sugano and Koizumi’s textbook and the findings that went into its production.
Here, the key is that Besley et al.’s research points to anomalous electrical and magnetic properties possessed by microclusters that are not seen either in molecules or in condensed matter:
And now, as we skip ahead to page 11 of Sugano et al.’s microcluster physics textbook, we come to section 1.3.1 entitled Fundamental Polyhedra.
This is where the connection between microclusters and the geometry of Johnson’s physics becomes readily apparent:
For one who has studied sacred geometry for many years, it is amazing to consider that at a level far too tiny for the naked eye, atoms are grouping together into perfect Platonic Solid formations.
It is also interesting to consider that some of these microclusters also have fluidlike qualities, allowing them to flow from one type of geometric structure into another. In their text, Sugano and Koizumi have assumed that certain polyhedra such as the icosahedron and dodecahedron are non-crystalline, and must therefore undergo a phase change before they could become a larger crystallized object.
However, later in this chapter we will present hard, irrefutable
evidence that the entire model of crystallography is flawed, and that under
certain circumstances, formations very similar to microclusters can be
formed at larger levels of size, from two or more atomic elements grouped
together.
If we took a
tetrahedron, for example, and constructed it out of a certain number of
marbles that all had an equal width, then we would need an exact “magic”
number of marbles to construct a tetrahedron of a given size. This is the
same as Buckminster Fuller’s model of “close-packed spheres,” and in its
simplest form is expressed by seeing that if you put three marbles together
into a triangle and then place a fourth marble above it in the middle, you
will see a tetrahedron form.
These images are taken by a scanning electron microscope at very high magnification, and the structure of the cuboctahedron geometry [Fig. 3.3, L] is clearly visible in a series of different angles. Interestingly, the cluster is seen to undergo different geometric changes from the cuboctahedron to other forms in its structure from image to image, again suggesting a fluidlike quality, and unseen “stresses” in the aether at work.
Figure 3.3 is an artist-rendered diagram of how the “magic number” of 459 spherical atoms will pack together to form a cuboctahedron-shaped cluster, whereas 561 atoms will cluster into the form of an icosahedron.
Figure 3.3 - Cuboctahedral cluster of 459 atoms (L) and Icosahedral cluster of 561 atoms (R)
Our next quote comes from section 3 of Besley et al.’s study, which discusses the “jellium” model and makes it very clear that the individual nature of the atoms in a microcluster is lost in favor of a group behavior.
Again we will see the mentioning of magic numbers and of electrons moving
through the entire structure instead of just through their parent atom; we
also see the hypothesis that “geometric shells” of electrons are somehow
formed in the microcluster.
The jellium model therefore explains cluster
magic numbers in terms of the filling of cluster electronic shells, which
are analogous to the electronic shells in atoms. For somewhat larger nuclearities (N ~ 100-1500 [total atoms in the cluster,]) there are periodic
oscillations in mass spectral peak intensities which have been attributed to
the bunching together of electronic shells into supershells.
Since there can be no individual electrons at this point, Besley et al. hypothesize the existence of “explicit angular-dependent many-body forces.” In short, a “fluid crystal” aetheric quantum model is essentially required to explain the forces that create microclusters:
As we think through the results of these microcluster studies, we must not forget that the Platonic Solids are very easily formed by vibrating a spherical area of fluid. It is quite surprising that the microcluster researchers do not appear to have noticed this connection.
The prevailing view of quantum mechanics as a particle phenomenon has such a strong hold on the minds of scientific researchers that elaborate explanations involving “geometric shells” of electrons must be invoked. The key question that must be addressed is how and why this geometry would form – and the idea of a vibrating, fluidlike quantum medium is by far the simplest answer.
A microcluster is simply a larger “aetheric atom” in a perfect geometric form.
DAVID HUDSON AND “ORMUS ELEMENTS”
Table 3.1 – Known Metallic Microclusters or “Ormus” Elements in David
Hudson’s patent.
Next, we introduce the work of David Hudson, who discovered a substance that turned out to contain microclusters in a goldmine on his property in the late 1970s.
He spent several million dollars having these mysterious materials analyzed and tested in various ways, and in 1989 Hudson patented his microcluster discovery by naming them Orbitally Rearranged Monatomic Elements, or “ORMEs.” [The name is usually changed to “Ormus” or “M-state” elements when discussed online so as not to interfere with Hudson’s copyrights.]
Hudson displays a broad knowledge of microcluster physics in
his published lectures from the early 1990s, but his findings are more
controversial than what we find in Sugano et al.’s textbook or other
published mainstream sources. Hudson’s patent focuses on the microcluster
structures he found in the following precious metal elements. (We should
note here that Sugano and Koizumi have established that microclusters have
been found in non-metallic elements as well.)
Hudson’s research demonstrated that these metallic microclusters are found throughout many different biological systems, including many different plants, and that they form up to 5% of the material in a calf’s brain by weight.
Furthermore,
Their physical qualities match the
descriptions of various materials in alchemical traditions from China,
India, Persia and Europe. Various people have volunteered to ingest gold microclusters or “monatomic gold,” and have reported experiencing the same
psychic effects as the kundalini changes noted in the
Vedic scriptures of
ancient India.
As the material is heated, its weight is
seen to increase by 300 percent or more. Even more surprisingly, as
microcluster iridium is heated to 850 degrees Celsius, the material
disappears from physical view and loses all of its weight. However, when the
temperature is again reduced, the microcluster iridium will reappear and
regain most of its former weight. In Hudson’s patent, he has a chart that
was generated by thermo-gravimetric analysis that shows this effect in
action.
Dr. Vladimir Ginzburg
suggested that an object’s mass is converted into pure field as it
approaches the speed of light, and Mishin and Aspden’s data suggests that
the mass is actually moving into a higher density of aetheric energy.
This harnessing of the vibrations of heat then creates extreme resonance at a lower relative temperature, bringing the internal vibrations of the iridium past the speed of light. (These internal vibrations may already be relatively close to the speed of light before such added resonance is introduced, due to the speed at which aether flows through the atomic “vortex” of negative electron clouds and the positive nucleus.) Then, when the threshold point of light-speed is finally reached, the aetheric energy of the iridium is displaced into a higher density, thus causing it to disappear from measurable view.
When the temperature is reduced, the iridium
again displaces back down into our own density, since the pressure that was
holding it in the higher density has now been eliminated.
ANOMALIES OF CRYSTAL FORMATION
Two hydrogen atoms and one oxygen atom form together in the shape of a tetrahedron to create the water molecule, (which is not a crystal in the liquid state but has a tetrahedral molecule,) and fluorite crystals form the octahedron. Crystals that form with these properties will maintain the same orientation throughout themselves, and are symmetrical.
A more technical description is that crystals are,
Our key question to remember here would be, “Why do
spherical energy vortexes end up joining together in these characteristic
geometric angles and patterns?” The answer, of course, shall be found in our
understanding of the Platonic Solids as “harmonic” energy structures in the aether.
The term “translation” means that we rotate a specific object by an exact number of degrees, such as 180, which would form a “two-fold” crystal since there are two such translations in a 360-degree circle.
Thus, “translational repetition” means that that the basic structural element (atom or molecular group of atoms) making up a crystal can be rotated again and again in the same way to form the repeated pattern.
The technical term for such a regular
arrangement of atoms is periodicity, which means that a crystal is made up
of “some basic structural unit which repeats itself infinitely in all
directions, filling up all of space” within itself. The same structure (atom
or group of atoms) keeps repeating in the same, periodic way, hence the term
periodicity.
This led to a whole science of X-ray crystallography that was formalized by William H. and William L. Bragg, where the points of light are analyzed geometrically in relation to each other in order to determine what the structure of the true crystal actually is.
For seventy years after this
technology was developed, every diffraction diagram that had ever been
observed by mainstream scientists fit the periodicity model perfectly, which
led to the inevitable and apparently quite simple conclusion that all
crystals were an arrangement of single atoms as structural units.
Atoms are “supposed” to retain their own individual point-like identities and not merge with other atoms into a larger whole. Nevertheless, in terms of pure geometry, the dodecahedron has 5-fold symmetry and the icosahedron has 5- and 10-fold symmetry.
These Platonic Solids fit all the requirements for symmetry as outlined by Dr. Wolff earlier in this chapter, but you simply cannot pack single atoms together to make either of these shapes. So again, the dodecahedron and icosahedron have symmetry, but they do not have periodicity as crystal formations.
Therefore, there was no provision in science to believe that either of these forms would appear as a molecular, crystalline structure – it was “impossible.”
Or so they thought…
Similar to microclusters but on a larger level of size, these quasi-crystals were discovered to have many strange properties, such as extreme strength, extreme resistance to heat and being non-conductive to electricity, even if the metals involved in their creation would normally act as conductors! (This will be explained as we progress.)
Unlike microclusters, which only appear to be able to be formed individually from “cluster beams”, quasi-crystals can be grouped together into usable alloys.
Fouche states the following on his website, with our added emphasis:
Arguably after 35 years of secret research on the Roswell hardware, those who had recovered these technologies still had hundreds if not thousands of unanswered questions about what they had found, and it was deemed “safe” to quietly introduce “quasi-crystals” to the non-initiated scientific world.
There are now literally thousands of different references to quasi-crystals on the Internet, completely separate from any mention of microclusters. (Not a single scientific study that we have been able to find online mentions both microclusters and quasi-crystals in the same document.) Many of the quasi-crystal references are from companies that are government contractors, and it is very easy to see that they are being studied with widespread intensity.
However, they are almost never mentioned in the general media,
even though they present such a unique challenge to our prevailing theories
of quantum physics. The research goes on, but it is with a very subdued
excitement.
In the image to the right of Figure 3.4, we can clearly see a number of pentagons, indicating the five-fold symmetry of the icosahedron:
"click" image to see multimedia
Figure 3.4 – The Icosahedron (L) and its X-ray diffraction diagram from a
quasi-crystal formation (R).
As we said, with the advent of quasi-crystals, both the dodecahedron and icosahedron appear, along with other unusual geometric forms, completing the appearance of all five of the Platonic Solids in the molecular realm in some way.
Both the dodecahedron and icosahedron possess elements of five-fold symmetry with their pentagonal structures.
Figure 3.5, from An Pang Tsai of NRIM in Tsukuba, Japan, shows an Aluminum-Copper-Iron quasi-crystal alloy in the shape of a dodecahedron and an Aluminum-Nickel-Cobalt alloy in the shape of a decagonal (10-sided) prism:
Figure 3.5 – Dodecahedral (L) and decagonal prism (R) quasi-crystals created by An Pang Tsai of NRIM.
The problem here is that you cannot create such crystals by using single atoms bound together, yet as we can see in the photographs, they are very real. The key problem for scientists, then, is how to explain and define the process by which these crystals are forming.
According to A.L. Mackay, one of the ways to include five-fold symmetry in a crystallographic definition is “Abandonment of Atomicity:”
What this suggests is that similar to microclusters, quasi-crystals appear to not have individual atoms anymore, but rather that the atoms have merged into a unity throughout the entire crystal.
While this may seem impossible
for crystallographers to believe, it is actually among the simplest of A.L.
Mackay’s four potential solutions to the problem, as it involves simple
three-dimensional geometry and correlates with our microcluster
observations. Again, since the crystals are very real, the only major hurdle
to cross is our fixation on the belief that atoms are made of particles.
All the atoms are measured
to vibrate at the exact same frequency and travel at the same speed, and all
appear to be located in the same area of space. Rigorously, the various
parts of the system act as a unified whole, losing all signs of
individuality. It is this very property that is required for a
“superconductor” to exist. (A superconductor is a substance that conducts
electricity with no loss of current.)
In
the case of the laser, the entire light beam behaves as if it were one
single “photon” in space and time – there is no way to differentiate
individual photons in the laser beam. It is interesting to note that lasers,
superconductors and quasi-crystals were all found in
recovered ET
technologies since the 1940s.
We will discuss this in later chapters that will deal with aetheric biology.
Figure 3.6 –
Dan Winter’s reprint of Sir William Crookes’ geometric Table of
the Elements.
Our next question concerns the “electron clouds” that have been seen in the atom.
Both Rod Johnson and
Dan Winter have noted that the teardrop-shaped
“electron clouds” in the atom will all fit perfectly together with the faces
of the Platonic Solids. Winter refers to the electron clouds as “vortex
cones,” and Figure 3.6 is an unfortunately illegible copy of the Periodic
Table of the Elements as originally devised by Sir William Crookes, a
well-known and highly respected scientist from the early 20th century who
later became an investigator into the field of parapsychology. At the bottom
of the image, we see an illustration of how the “vortex cones” fit on each
face of the Platonic Solids.
The chart is obviously read from the top down, and the first element that is written out below the two circles in the center is Helium, and the line then moves to each successive element. The scale to the left is a series of degree measurements, beginning with 0 at the top line and counting by units of 10° for each line.
The degree numbers written in on the scale are 50, 100, 150,
200, 250, 300, 350 and 400. This appears to indicate that Sir Crookes’
theory involved set angular rotations or translations of the elements in
terms of their geometry as we move from one element to the next. We can see
that the wave is mostly straight, but at times there are “dips” in the line
that appear to correspond to larger angular rotations that must be made.)
There are “nests” of
Platonic Solids in the
atom, one solid for each major sphere in the “nest”, just as there are
“nests” of electron clouds at different levels of valence that all co-exist.
The Platonic Solids form an energetic structure and framework that the aetheric energy must flow through as it rushes towards the low-pressure
positive center of the atom. Thus, we see each face of the Solids acting as
a funnel that the flowing energy must pass through, creating what Winter
called “vortex cones.”
Given what we have
seen with the comprehensive research that has gone on, especially with
quasi-crystal engineering, it appears that this information is already in
use by humanity in certain circles.
|
||||||||||||||||||||||||||||