|
by Anil Ananthaswamy
for
Quanta Magazine researchers can now preemptively fine-tune artificial neural networks, saving some of the time and expense of training.
When deep neural
networks, a form of
AI (artificial intelligence) that learns to discern patterns in data,
began surpassing traditional algorithms 10 years ago, it was because
we finally had enough data and processing power to make full use of
them.
Training them requires carefully tuning the values of millions or even billions of parameters that characterize these networks, representing the strengths of the connections between artificial neurons.
The goal is to find nearly ideal values for them, a process known as optimization, but training the networks to reach this point isn't easy.
That may soon change.
Boris Knyazev of the University of Guelph in Ontario and his colleagues have designed and trained a "hypernetwork" - a kind of overlord of other neural networks - that could speed up the training process.
Given a new, untrained deep neural network designed for some task, the hypernetwork predicts the parameters for the new network in fractions of a second, and in theory could make training unnecessary.
Because the hypernetwork learns the extremely complex patterns in the designs of deep neural networks, the work may also have deeper theoretical implications.
For now, the hypernetwork performs surprisingly well in certain settings, but there's still room for it to grow - which is only natural given the magnitude of the problem.
If they can solve it,
Getting Hyper
Currently, the best methods for training and optimizing deep neural networks are variations of a technique called stochastic gradient descent (SGD).
Training involves minimizing the errors the network makes on a given task, such as image recognition. An SGD algorithm churns through lots of labeled data to adjust the network's parameters and reduce the errors, or loss.
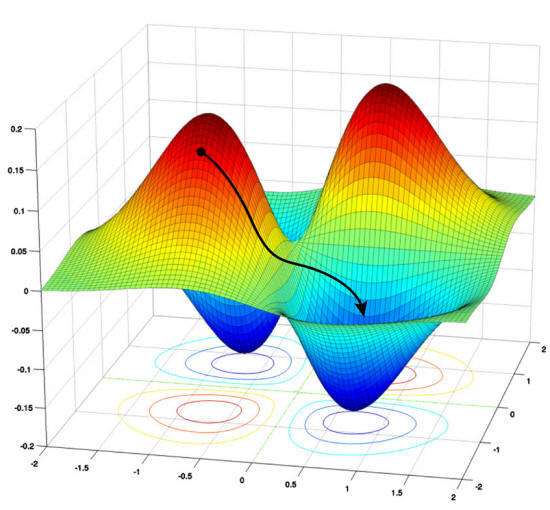
Gradient descent is the iterative process of climbing down from high values of the loss function to some minimum value, which represents good enough (or sometimes even the best possible) parameter values.
But this technique only works once you have a network to optimize.
To build the initial neural network, typically made up of multiple layers of artificial neurons that lead from an input to an output, engineers must rely on intuitions and rules of thumb.
These architectures can vary in terms of the number of layers of neurons, the number of neurons per layer, and so on.
Gradient descent takes a network down its "loss landscape," where higher values represent greater errors, or loss.
The algorithm tries to find the global minimum value to minimize
loss.
One can, in theory, start with lots of architectures, then optimize each one and pick the best.
It'd be impossible to train and test every candidate network architecture.
So in 2018, Mengye Ren, along with his former University of Toronto colleague Chris Zhang and their adviser Raquel Urtasun, tried a different approach.
They designed what they called a graph hypernetwork (GHN) to find the best deep neural network architecture to solve some task, given a set of candidate architectures.
The name outlines their approach.
Here's how it works.
Ren's team showed that this method could be used to rank candidate architectures and select the top performer.
When Knyazev and his colleagues came upon the graph hypernetwork idea, they realized they could build upon it.
In their new paper, the team shows how to use GHNs not just to find the best architecture from some set of samples, but also to predict the parameters for the best network such that it performs well in an absolute sense.
And in situations where the best is not good enough, the network can be trained further using gradient descent.
Training the Trainer
Knyazev and his team call their hypernetwork GHN-2, and it improves upon two important aspects of the graph hypernetwork built by Ren and colleagues.
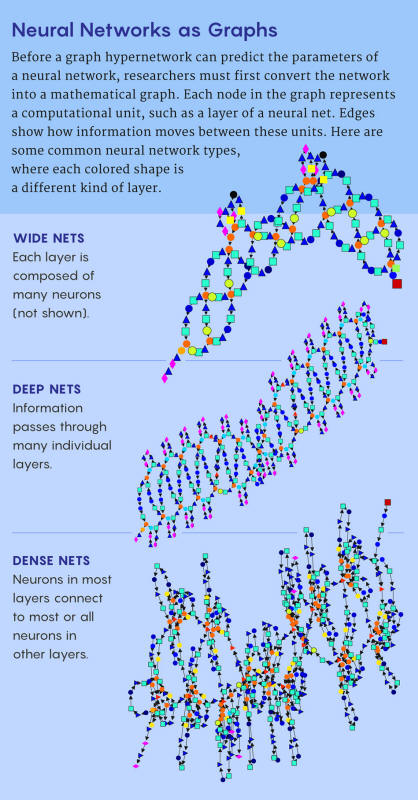
First, they relied on Ren's technique of depicting the architecture of a neural network as a graph. Each node in the graph encodes information about a subset of neurons that do some specific type of computation.
The edges of the graph depict how information flows from node to node, from input to output.
The second idea they drew on was the method of training the hypernetwork to make predictions for new candidate architectures.
This requires two other neural networks:
These two networks also have their own parameters, which must be optimized before the hypernetwork can correctly predict parameter values.
Samuel Velasco Quanta Magazine source: arxiv.org/abs/2110.13100
To do this, you need training data - in this case, a random sample of possible artificial neural network (ANN) architectures.
For each architecture in the sample, you start with a graph, and then you use the graph hypernetwork to predict parameters and initialize the candidate ANN with the predicted parameters.
The ANN then carries out some specific task, such as recognizing an image.
You calculate the loss made by the ANN and then - instead of updating the parameters of the ANN to make a better prediction - you update the parameters of the hypernetwork that made the prediction in the first place.
This enables the hypernetwork to do better the next time around.
Now, iterate over every image in some labeled training data set of images and every ANN in the random sample of architectures, reducing the loss at each step, until it can do no better.
At some point, you end up with a trained hypernetwork.
Knyazev's team took these ideas and wrote their own software from scratch, since Ren's team didn't publicize their source code. Then Knyazev and colleagues improved upon it.
For starters, they identified 15 types of nodes that can be mixed and matched to construct almost any modern deep neural network. They also made several advances to improve the prediction accuracy.
Most significantly, to ensure that GHN-2 learns to predict parameters for a wide range of target neural network architectures, Knyazev and colleagues created a unique data set of 1 million possible architectures.
As a result, GHN-2's predictive prowess is more likely to generalize well to unseen target architectures.
Impressive Results
The real test, of course, was in putting GHN-2 to work.
Once Knyazev and his team trained it to predict parameters for a given task, such as classifying images in a particular data set, they tested its ability to predict parameters for any random candidate architecture.
This new candidate could have similar properties to the million architectures in the training data set, or it could be different - somewhat of an outlier. In the former case, the target architecture is said to be in distribution; in the latter, it's out of distribution.
Deep neural networks often fail when making predictions for the latter, so testing GHN-2 on such data was important.
Armed with a fully trained GHN-2, the team predicted parameters for 500 previously unseen random target network architectures. Then these 500 networks, their parameters set to the predicted values, were pitted against the same networks trained using stochastic gradient descent.
The new hypernetwork often held its own against thousands of iterations of SGD, and at times did even better, though some results were more mixed.
Boris Knyazev of the University of Guelph in Ontario has helped build a hypernetwork that's designed
to predict the parameters for an untrained neural network. For a data set of images known as CIFAR-10, GHN-2's average accuracy on in-distribution architectures was 66.9%, which approached the 69.2% average accuracy achieved by networks trained using 2,500 iterations of SGD.
For out-of-distribution architectures, GHN-2 did surprisingly well, achieving about 60% accuracy.
In particular, it achieved a respectable 58.6% accuracy for a specific well-known deep neural network architecture called ResNet-50.
GHN-2 didn't fare quite as well with ImageNet, a considerably larger data set:
Still, this compares favorably with the average accuracy of 25.6% for the same networks trained using 5,000 steps of SGD.
(Of course, if you continue using SGD, you can eventually - at considerable cost - end up with 95% accuracy.)
Most crucially, GHN-2 made its ImageNet predictions in less than a second, whereas using SGD to obtain the same performance as the predicted parameters took, on average, 10,000 times longer on their graphical processing unit (the current workhorse of deep neural network training).
And when GHN-2 finds the best neural network for a task from a sampling of architectures, and that best option is not good enough, at least the winner is now partially trained and can be optimized further.
Instead of unleashing SGD on a network initialized with random values for its parameters, one can use GHN-2's predictions as the starting point.
Beyond GHN-2
Despite these successes, Knyazev thinks the machine learning community will at first resist using graph hypernetworks.
He likens it to the resistance faced by deep neural networks before 2012. Back then, machine learning practitioners preferred hand-designed algorithms rather than the mysterious deep nets.
But that changed when massive deep nets trained on huge amounts of data began outperforming traditional algorithms.
In the meantime, Boris Knyazev sees lots of opportunities for improvement.
For instance, GHN-2 can only be trained to predict parameters to solve a given task, such as classifying either CIFAR-10 or ImageNet images, but not at the same time.
In the future, he imagines training graph hypernetworks on a greater diversity of architectures and on different types of tasks (image recognition, speech recognition and natural language processing, for instance).
Then the prediction can be conditioned on both the target architecture and the specific task at hand.
And if these hypernetworks do take off, the design and development of novel deep neural networks will no longer be restricted to companies with deep pockets and access to big data.
Anyone could get in on the act. Knyazev is well aware of this potential to "democratize deep learning," calling it a long-term vision.
However, Petar Veličković highlights a potentially big problem if hypernetworks like GHN-2 ever do become the standard method for optimizing neural networks.
With graph hypernetworks, he said,
Of course, this is already largely the case for neural networks.
Thomas Kipf, however sees a silver lining.
GHN-2 showcases the ability of graph neural networks to find patterns in complicated data.
Normally, deep neural networks find patterns in images or text or audio signals, which are fairly structured types of information.
GHN-2 finds patterns in the graphs of completely random neural network architectures.
And yet, GHN-2 can generalize - meaning it can make reasonable predictions of parameters for unseen and even out-of-distribution network architectures.
If that's the case, it could lead to a new, greater understanding of those 'black boxes'...
|