5º  EXPLORANDO EL MUNDO DE LAS MARGARITAS

“Dadme en cualquier momento un error provechoso, lleno de interrogantes, repleto de sus propias correcciones.”
Vilfredo Pareto

comentario sobre Kepler

La palabra teoría tiene la misma raíz griega que teatro. Ambas están relacionadas con la exhibición en un escenario.

En ciencia una teoría no es más que lo que le parece a su autor, una manera plausible de vestir los hechos y presentarlos a la audiencia. Como las obras de teatro, las teorías se juzgan de acuerdo con varios criterios diferentes y escasamente conectados. El contenido artístico es importante; una teoría que es elegante, sugestiva y está presentada con habilidad es apreciada universalmente.

Sin embargo, a los científicos muy trabajadores les gustaban las teorías repletas de predicciones que pueden ser comprobadas fácilmente. Tiene poca importancia si el punto de vista del teorizador es correcto o incorrecto: se estimula la investigación y la búsqueda, se descubren hechos nuevos, y se componen teorías nuevas.

Estar equivocado no supuso un demérito importante para la teoría de la creación continua de los astrónomos Hoyle, Bondi y Gold. Ahora la idea ha sido abandonada, pero en su día se trataba de un concepto intelectualmente satisfactorio. Las únicas teorías malas son aquellas que no pueden ser cuestionadas o evaluadas.

¿De qué sirve una teoría que diga que el universo fue creado de forma completa, con habitantes y todos con memoria de un pasado no existente, a las 15:37 horas el día 27 de octubre de 1917? No hay manera de probarlo o rechazarlo, y no proporciona predicciones útiles.

En una primera impresión, la hipótesis de Gaia puede parecer no comprobable. Evidentemente, sería impropio e irresponsable intentar llevar a cabo la vivisección de un planeta vivo. Afortunadamente ya ha pasado de moda el estilo utilizado en el siglo XIX para la investigación de las cosas vivas: «con sangre hasta los codos». Hemos aprendido de los ingenieros, que valoran sus artilugios mucho más de lo que la mayoría de nosotros valoramos los mecanismos infinitamente más complejos y hermosos de los organismos vivos.

Ellos nos han enseñado que se puede aprender mucho acerca de un sistema a partir de pruebas no invasivas, que la vivisección no es necesaria. Por tanto, la teoría de Gaia está abierta a varios modos de investigación experimental.

La evidencia más directa proviene del mundo real tal como es ahora. De manera semejante al hecho de que podemos comprobar el pulso, la presión sanguínea y la actividad eléctrica del corazón sin interferir en la fisiología normal del sujeto humano, también podemos observar el comportamiento del aire, los océanos y las rocas. Podemos medir el pulso estacional del dióxido de carbono en el aire y comprender cómo las plantas lo respiran e incorporan, mientras los consumidores lo respiran y expulsan.

Podemos seguir el trayecto de los nutrientes esenciales desde las rocas al océano, al aire y vuelta a empezar. También podemos apreciar cómo sistemas diferentes pero interrelacionados se encuentran implicados en cada paso.

Además de ello, disponemos de una enorme cantidad de evidencias históricas preservadas en las rocas. Durante su lapso de vida nuestro planeta ha sufrido el impacto de asteroides. Hemos sido golpeados por unos treinta planetas pequeños, de hasta 16 kilómetros de diámetro, que viajaban a una velocidad de seis veces la del sonido.

Estos impactos liberan una cantidad de energía equivalente a unos miles de veces la energía que sería liberada si todas las cabezas nucleares estacionadas en los almacenes de armas actuales explotasen al mismo tiempo. Estos acontecimientos producen algo más que cráteres de 320 kilómetros; pueden destruir hasta el 90 por ciento de todos los organismos vivos, desde los microscópicos hasta los macroscópicos.

Los impactos hacen sonar la Tierra como una campana, y las reverberaciones del acontecimiento resuenan, metafóricamente hablando, a lo largo de todos los sistemas de la Tierra por un período de quizás un millón de años o más. La historia de nuestro planeta está marcada por estas perturbaciones; a partir del registro de las mismas podemos aprender mucho sobre cómo funciona el sistema y cómo se reestablece la homeostasis completa.

Si se duda de que la Tierra haya sido golpeada tan a menudo, basta con mirar el mapa de distribución de cráteres en las antiguas capas rocosas del Canadá (figura 3.1). Es como echar un vistazo a una región de la superficie lunar.

Sin embargo, en la mayor parte de las áreas continentales, y en toda la superficie del fondo del mar, la rapidez de los procesos de erosión allanadores y la expansión del fondo oceánico ocultan rápidamente la evidencia de todos los impactos, excepto los que corresponden a los más recientes.

3.1.

Mapa del Canadá donde se muestran los cráteres producidos por impactos de meteoritos.

No todos los acontecimientos catastróficos son producidos por causas externas; algunos, como la aparición de oxígeno en forma de gas, son generados por tensiones internas inherentes al sistema, y pueden ser comparados a las crisis de los organismos vivos, tales como la pubertad, la menopausia o la metamorfosis de una oruga en mariposa. El registro de las rocas, aunque difuminado por el tiempo y a menudo incompleto, todavía preserva alguna evidencia del estado físico y químico de la Tierra y de la distribución de especies antes y después de cada una de estas perturbaciones.

Sin embargo, desenredar el registro es como intentar encontrar trazas de la identidad de un terrorista a partir de los escombros del edificio que su bomba ha destruido.

La crítica más convincente a la teoría de Gaia plantea que el concepto de homeostasis planetaria, por y para los organismos vivos, es imposible porque requiere la evolución de algún tipo de comunicación entre las especies, además de una capacidad de previsión y planeamiento. Los autores de esta crítica desafiante, y para mí útil, no tienen en cuenta la evidencia empírica de que la Tierra ha mantenido un clima favorable para la vida a pesar de las mayores perturbaciones, o que la atmósfera tiene una composición estable a pesar de la incompatibilidad química de sus gases componentes.

Desde la certeza de sus conocimientos en biología dicen que nunca podría existir un organismo tan grande y, tal como lo ven, tan estable. Pienso que esta crítica es dogmática, y, como vimos en el capítulo anterior, fácilmente rebatible. El modelo simple del mundo de las margaritas ilustra cómo podría funcionar Gaia. Partíamos de un mundo imaginario que gira como la Tierra y que es calentado por una estrella gemela a nuestro Sol durante su movimiento orbital.

En este mundo, la competición por el territorio de dos especies de margaritas, una oscura y la otra clara, da lugar a una regulación exacta de la temperatura planetaria en el nivel apropiado para el desarrollo de estas plantas. No es necesaria ninguna previsión, ni planificación, ni propósito preestablecido. El mundo de las margaritas es una aproximación teórica a un planeta en homeostasis. Ahora podemos empezar a pensar en Gaia como una teoría, algo más que el simple «supongamos» de una hipótesis.

En el mundo de las margaritas hay mucho más que una respuesta a una crítica. Lo desarrollé, en primer lugar, con este propósito, pero cuando avanzaba en su planteamiento percibí que, además de las cuestiones acerca de Gaia, era una fuente de investigación y una respuesta a preguntas relativas a la ecología teórica y el darwinismo. Una propiedad importante del modelo es su docilidad y estabilidad en términos matemáticos.

Cuando lo desarrollé comprobé que el número de especies que se puede incluir en él sólo parece estar limitado por la capacidad de los ordenadores utilizados y por la paciencia del investigador.

Independientemente de los detalles, los procesos de realimentación ambientales estabilizan el sistema de ecuaciones diferenciales que describe el crecimiento y la competición entre especies. Una gran parte de lo que sigue a continuación es el relato de mis exploraciones en el mundo de las margaritas, un informe de mis descubrimientos en él. He considerado que la mayoría de mis lectores no se sienten motivados por las expresiones matemáticas y, por tanto, no las incluyo. Para los que crean que cualquier teoría que no sea expresada en el lenguaje puro de las matemáticas es inadecuada, Andrew Watson y yo hemos descrito las matemáticas del mundo de estas plantas en nuestro trabajo en Tellus.

La estabilidad de dicho mundo no depende en ningún modo de una selección precisa de condiciones iniciales, o de tasas de crecimiento, y, tal como veremos en los últimos capítulos, el modelo es general en su aplicación.

Algunos de los diagramas utilizados para ilustrar la geofisiología del modelo planetario pueden ser difíciles de seguir para lectores no familiarizados con esta forma de expresión gráfica. He escrito este libro para vosotros, o sea que podéis saltaros este capítulo siempre que ya estéis convencidos de que la teoría de Gaiga proporciona una representación bastante aproximada de la Tierra. Sin embargo, pido a mis detractores que lo lean, porque intentaré replicar aquí con detalle a las objeciones que han planteado.

La reacción de los científicos ante el mundo de las margaritas fue reveladora. Los más interesados fueron los meteorólogos y climatólogos y, en segundo lugar, los geólogos y geoquímicos. Los biólogos, con raras excepciones, o bien ignoraron los modelos o siguieron tan escépticos como antes. Una objeción señalada de manera persistente por los biólogos era que, en el mundo real, las margaritas tendrían que usar algo de su energía para fabricar pigmentos, lo que las colocaría en desventaja con respecto a hipotéticas margaritas grises no pigmentadas. No hubiera sido posible la regulación de temperatura en semejante mundo.

Tal como lo expresaron, “las margaritas grises hubieran hecho trampa”.

Animado por sus críticas construí un modelo con tres especies de margaritas. Todo lo que el nuevo modelo requería era una nueva serie de ecuaciones diferenciales para describir la temperatura y crecimiento de la especie de margaritas grises. Se trataba de introducir margaritas de clase media discretamente ataviadas en un mundo de colores extremos.

Atribuí a las margaritas oscuras y claras una rebaja en la tasa de crecimiento de un uno (1%) por ciento por la fabricación de pigmentos. Estoy satisfecho de poder afirmar que el cínico parecer de los biólogos no se ve confirmado por este nuevo modelo. Así se puede observar en la figura 3.2. De nuevo se ha establecido que la luminosidad aumenta desde el 60 al 140 por ciento de la de nuestro Sol. Las poblaciones de margaritas se encuentran en el cuadro superior, con las oscuras a la izquierda, las grises en medio y las claras a la derecha.

El hecho de que las margaritas grises no gasten energía en la fabricación de pigmentos no les sirve de nada cuando su mundo es demasiado caliente o demasiado frío para que crezcan.

3.2.

La evolución del clima en un mundo de margaritas con tres especies: margaritas negras, grises y blancas. A modo de comparación, la línea de trazos del cuadro inferior representa la evolución de la temperatura en ausencia de vida.

Pero las margaritas negras pueden florecer en el frío y las blancas en el calor. Las margaritas grises proliferan cuando el clima es templado y no se precisa regulación. En otras palabras, las diferentes especies crecen cuando ellas y su medio ambiente están adaptados el uno con el otro.

Para contestar a las críticas hubiera sido suficiente con añadir margaritas grises. Sin embargo, una vez metido en la tarea, encontré que era igualmente fácil hacer un modelo que pudiese acomodar cualquier número de margaritas diferentes, por ejemplo de uno a veinte. Construí entonces un modelo en el que, cualquiera que fuera el número de especies los tonos de las margaritas variasen a incrementos constantes desde los más oscuros a los más claros.

En la figura 3.3 se muestra la evolución de la temperatura, de las poblaciones de margaritas y otras propiedades de un mundo con veinte especies distintas. Como en el modelo de tres especies, se trata de un mundo cuya estrella se calienta a medida que envejece. El cuadro inferior muestra la evolución de la temperatura planetaria; el cuadro intermedio, la evolución de las poblaciones de las diferentes especies y el cuadro superior, la biomasa total y la diversidad del ecosistema representado en el modelo.

La diversidad del ecosistema es tanto mayor cuanto menor es la dificultad. Cuando el calor del Sol es exactamente el adecuado y no hace falta ningún esfuerzo para la regulación de la temperatura, entonces puede coexistir el mayor número de especies. Cuando el sistema se encuentra bajo alguna dificultad, cuando ha empezado a evolucionar o está agonizando, la diversidad es mínima y la población la constituyen casi enteramente las especies más oscuras o más claras.

Efectivamente, si alguna especie está en situación ventajosa en esos períodos es la más oscura o la más clara, pero nunca las grises.

Sin embargo, todavía hay muchos otros aspectos en este nuevo modelo con los que rebatir las críticas de los biólogos más escépticos. Cuando lo armaba aún no conocía la ecología teórica, esa rama de la biología matemática que trata de las interacciones entre las especies de un ecosistema. Como veremos, el mundo de las margaritas proporciona una salida a una ciencia que ha estado coartada durante años por las limitaciones de sus teorías.

En los años veinte, los biomatemáticos Lotka y Volterra introdujeron su famoso modelo de competencia entre conejos y zorros. Era un modelo simple, como el del mundo de las margaritas, pero difería de éste en la medida que el medio ambiente se consideraba infinito y neutral. El crecimiento de conejos o zorros no afectaba al medio ambiente, y no se permitían cambios ambientales que pudiesen afectar a sus poblaciones.

El significado de las dos ecuaciones de este modelo puede expresarse como sigue: los zorros aumentan cuando el número de conejos crece, pero los conejos disminuyen cuando el de zorros aumenta. En esta relación hay un punto estable donde las dos especies coexisten en una proporción constante, excepto en el caso de una mala época que mate algunos conejos. Efectivamente, cualquier cambio de población que no provenga del interior del mismo modelo condena a este mundo simple a una fluctuación cíclica y nunca puede volver a una relación estable.

Observemos cómo ocurre.

Si una epidemia produce la muerte repentina de conejos, a continuación se producirá la muerte de zorros por falta de alimento. Los conejos se reproducen más rápidamente y pronto su población será superior al que había antes de la plaga. Pero ahora los zorros también empiezan a crecer, y la velocidad de crecimiento de los conejos se amortigua y disminuye cuando el incremento del número de zorros los amenaza.

Enseguida los conejos son demasiado escasos para alimentar a los zorros, los zorros mueren y el ciclo empieza de nuevo.

¿Explica este modelo las oscilaciones de población que se observan en la Naturaleza? Sí, lo hace.

Los ecólogos de campo han mostrado que en los ecosistemas simples se producen ciclos de poblaciones, pero al examinarlas más de cerca, nos parece que las observaciones de campo siempre se han realizado en ecosistemas enfermos o preparados por el hombre donde sólo unas pocas especies interaccionan entre sí, y donde sólo se consideran dos especies (por ejemplo plagas atacando la vegetación de un monocultivo agrícola, o enfermedades bacterianas de plantas y animales).

Estos ejemplos de dos especies, en las que las poblaciones siguen ciclos periódicos o fluctúan de una manera caótica e impredecible, pueden ser reproducidos con éxito por los sucesores matemáticos del famoso modelo de zorros y conejos de Lotka y Volterra.

Lo que estos modelos ecológicos y la propia teoría ecológica como ciencia han sido incapaces de explicar es la gran estabilidad de los ecosistemas naturales complejos como las selvas tropicales o, en otras palabras, resolver el acertijo de Darwin:

«¿En qué lugar el viento mueve el tomillo silvestre y crecen las acederillas y la vacilante violeta?».

Los ecólogos han intentado vencer los inconvenientes de sus modelos sencillos incluyendo jerarquías estructuradas de especies que llaman «redes tróficas». En estas jerarquías hay una pirámide en cuya cúspide se encuentra el predador más alto, como por ejemplo el León, que presenta el menor número de individuos. Las poblaciones aumentan a medida que se desciende en cada nivel «trófico», hasta la base de la pirámide en que se encuentran los productores primarios más numerosos, las plantas, que proporcionan alimento para todo el sistema.

A pesar de los años de esfuerzo y el tiempo empleado en el cálculo, los ecólogos no han hecho ningún progreso real en el modelo teórico de un ecosistema natural complejo, como una selva húmeda tropical o el ecosistema tridimensional del océano.

Ningún modelo diseñado desde la ecología teórica puede explicar en términos matemáticos la estabilidad manifiesta de sistemas naturales tan amplios.

En efecto, el distinguido ecólogo, Robert May, en su libro Theoretical Ecology [Ecología teórica], escribe en el capítulo titulado «Modelos de ecosistemas con varias especies»:

«Cuando se realizan esta clase de estudios, una gran variedad de modelos matemáticos sugieren que cuando un sistema es más complejo, en el sentido de un mayor número de especies con una estructura más rica, de interdependencias, dinámicamente resulta más frágil... Entonces la generalización matemática sugiere que el incremento de complejidad conlleva fragilidad dinámica en lugar de resistencia».

May sigue escribiendo:

«Ello no quiere decir que en la naturaleza los sistemas complejos deban parecer menos estables que los sencillos. Tanto a un sistema complejo en un medio ambiente caracterizado por un nivel bajo de fluctuaciones aleatorias como a un sistema sencillo en un medio ambiente caracterizado por un nivel alto de fluctuaciones aleatorias, puede corresponderles la misma probabilidad de sobrevivir, cada uno teniendo la estabilidad dinámica apropiada a su medio ambiente... Una conclusión general importante es que las grandes e inauditas perturbaciones impuestas por el hombre serán probablemente más traumáticas para los ecosistemas complejos que para los sencillos.

 

Ello invierte el punto de vista inocente, aunque bien intencionado, de que "complejidad conlleva estabilidad" y su moraleja asociada de que tendríamos que preservar, e incluso crear, ecosistemas complejos como tampones contra las agresiones del hombre. Yo diría que los ecosistemas naturales complejos que se encuentran amenazados en las zonas tropicales y subtropicales son menos capaces de aguantar nuestros azotes que los sistemas relativamente simples de las zonas templadas y boreales».

Esta negación reconoce la estabilidad de los ecosistemas complejos en el mundo real. Sin embargo, deja la impresión de que la diversidad es, en general, una desventaja, y que la naturaleza, no teniendo en cuenta las elegantes matemáticas de la biología teórica, de alguna manera ha hecho trampa.

Evidentemente si hubiera conocido estos trabajos nunca hubiera intentado desarrollar algo tan tonto como un modelo con veinte especies de margaritas. Afortunadamente para mí fui educado en aquella escuela científica que propone la lectura de los libros científicos mucho después de haber realizado los experimentos.

Entonces, ¿qué es lo que confiere la gran estabilidad y ausencia de cualquier comportamiento cíclico o caótico a los modelos del mundo de las margaritas?

La respuesta es que las margaritas nunca pueden crecer de manera incontrolada; si lo hacen, el ambiente se hace desfavorable y se acota el crecimiento. De manera semejante, el medio ambiente no puede desplazarse hacia estados desfavorables en presencia de las margaritas; el crecimiento en respuesta de las margaritas del color apropiado lo evita. Es el acoplamiento estrecho entre estas relaciones, que condiciona tanto el crecimiento de las margaritas como la temperatura planetaria, lo que hace que el modelo funcione.

Quizá nuestra experiencia puede representarse mediante la metáfora de que la familia y la sociedad funcionan mejor cuando existen reglas firmes, pero aplicadas en su justa medida, que cuando existe una libertad ilimitada.

Interesado en ver si estas interpretaciones eran correctas construí un mundo de margaritas adicional. En éste, las margaritas eran comidas por conejos y los conejos a su vez eran comidos por zorros, una combinación del modelo de Lotka y Volterra con el mundo de las margaritas. Para evaluar la estabilidad de este modelo más complejo lo sometí a catástrofes periódicas; en cuatro ocasiones durante la evolución del modelo, el 30 por ciento de la población de margaritas fue destruida inmediatamente, como por una epidemia, y el sistema permitió que se recuperaran (figura 3.4).

Sorprendentemente, ni la adición de herbívoros ni las plagas afectan seriamente a la capacidad de las margaritas para regular el clima. Durante el curso normal de la evolución todas las poblaciones son estables y se recuperan pronto de las perturbaciones de las epidemias. Finalmente, el sistema ya no puede compensar el siempre creciente flujo de energía solar y se pierde. Como es de esperar, cuanto más cerca se encuentra del final más grande es el efecto de las perturbaciones.

La diferencia entre el punto de vista geofisiológico y el ecológico reside en la interpretación de la perturbación. El geofisiológico entiende la temperatura, la lluvia, el aporte de nutrientes, etcétera, como variables que pueden ser modificadas. Desde su punto de vista el sistema gaiano evoluciona junto con su medio ambiente químico y físico y está bien capacitado para afrontar cambios de esta naturaleza.

Por ejemplo, las selvas de los trópicos húmedos están generalmente bien provistas de agua y sombra gracias a su cubierta de nubes; durante su existencia nunca se encuentran sometidas a una sequía prolongada como en una región desértica.

3.4.

El mundo de las margaritas con conejos y zorros, perturbado por cuatro epidemias que mataron el 30 por ciento de las margaritas en cada caso.

Por el contrario, los ecólogos teóricos ignoran el medio ambiente físico y químico. Para ellos el medio ambiente significa el conjunto mismo de especies, y un nicho es una parte de territorio negociado entre las especies como si uno pudiera mirar indistintamente el medio ambiente de Suiza para comprender la gente de Italia, Francia y Alemania. Desde este punto de vista las perturbaciones consisten en competencia o guerras.

La invasión humana de una selva tropical con sierras mecánicas, y el consiguiente cambio de la masa forestal por ecosistemas agrícolas, es un hecho traumático. Es como destruir el ecosistema del modelo de las margaritas y reemplazarlo con un solo monocultivo de especies negras. Tanto en el mundo de las margaritas como en las selvas, este hecho podría conducir a una muerte prematura por sobrecalentamiento, especialmente si tiene lugar en un tiempo o en un lugar en que el Sol está caliente.

Los geofisiólogos y los ecólogos están de acuerdo en que los ecosistemas complejos no se recuperarán fácilmente de agresiones como ésta; en lo que difieren es en la evaluación de la estabilidad del monocultivo, o de la única especie de margaritas. La geofisiología dice que estos ecosistemas tienen una capacidad limitada de interaccionar con su ambiente físico, y por tanto son incapaces de mantener su medio ambiente cuando están expuestos a una perturbación grande.

Los trópicos húmedos han permanecido arbolados a pesar de cambios en el clima de la Tierra que en términos humanos pueden ser considerados como grandes, pero que son triviales a escala planetaria. La presencia de una gran diversidad de especies ayuda a esta gran capacidad para soportar el cambio climático.

En la mayoría de ejemplos del mundo de las margaritas se ha mostrado que el Sol aumenta constantemente su producción de calor, una perturbación externa que aumenta incesantemente su intensidad hasta que la vida ya no puede continuar. Una manera alternativa de ilustrar el mundo de las margaritas consiste en permitir que la vida transcurra normalmente a una intensidad constante de luz solar y entonces introducir súbitas perturbaciones tales como un cambio en el clima o alguna catástrofe como una epidemia o el impacto de un asteroide.

Así, en la figura 3.5 se muestra un mundo de margaritas con 10 especies coloreadas cuya existencia estable es alterada de pronto por una epidemia que mata el 60 por ciento de las margaritas sin reparar en el color.

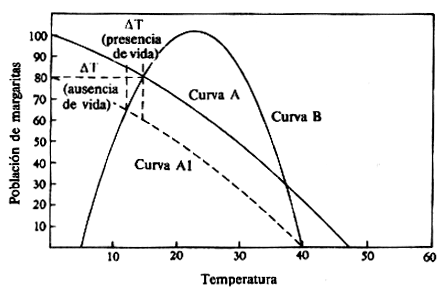
En el cuadro inferior, la línea a trazos representa la temperatura planetaria en ausencia de margaritas, a 40 °C se encuentra el límite para la vida. La línea continua muestra el clima con las margaritas presentes antes, durante y después de la perturbación. La temperatura se mantiene a unos 25 °C excepto cuando la epidemia golpea por primera vez la población de margaritas.

Cuando la perturbación cede el sistema rápidamente recupera el statu quo. El cuadro superior muestra la variación en la distribución de especies antes, durante y después de la catástrofe.

Aún bajo esta perturbación el sistema es reacio a desplazarse lejos del estado óptimo que existía antes del cambio. El efecto más notorio de la alteración se manifiesta en la distribución de las diferentes especies de margaritas.

La respuesta rápida del mundo de las margaritas al cambio requiere una realimentación positiva e implica el crecimiento explosivo de las especies cuya interacción con el clima es más favorable.

3.5.

Efecto en el clima de una plaga que mata el 60 por ciento de las margaritas en un mundo en que la luminosidad solar se mantiene a intensidad constante. Obsérvese cómo se recupera la homeostasis tanto en la población como en la temperatura durante y después de la perturbación.

Este modelo contiene 10 especies de margaritas distribuidos en un intervalo de colores uniforme y fijo desde el oscuro al claro.

Las mutaciones y la posibilidad de cambios evolutivos entre las especies constituyen un factor adicional a tener en cuenta. En este sentido, el cambio abrupto de la distribución de especies observado en el momento de la perturbación y de nuevo al final de la misma refleja la intensidad de la presión de selección en estos momentos. El modelo está fundamentalmente de acuerdo con las observaciones de Stephen Jay Gould y Niles Eldredge sobre la evolución puntuada.

En lugar de cambios estables y graduales, como en el punto de vista darwiniano convencional, hay períodos de evolución abrupta y rápida: las puntuaciones. La teoría de Gaia esperaría que la evolución del medio ambiente químico y físico y de las especies se produjera conjuntamente.

Habría períodos largos de homeostasis, con cambios pequeños en el medio ambiente y en la distribución de las especies, que serían interrumpidos por cambios súbitos de ambos órdenes.

3.6.

El efecto de una plaga periódica de intensidad constante sobre la capacidad de las margaritas para controlar el clima. Obsérvese cómo se amplifica el efecto de perturbación de la plaga en los momentos de máxima presión cerca del principio y del final de la vida del mundo de las margaritas.

 

El incremento de la amplitud de las oscilaciones en la última parte de la curva recuerda la evolución de las series actuales de períodos glaciares e interglaciares.

Estos períodos puntuales podrían ser originados internamente por la evolución de algunas especies poderosas, como el hombre, cuya presencia altera el medio ambiente, o el resultado de influencias externas tales como el impacto de asteroides.

Los experimentos de perturbación y de cambio progresivo pueden ser combinados en uno solo, tal como se muestra en la figura 3.6. Aquí nuestro mundo de 10 especies de margaritas evoluciona como al principio, pero ahora se produce una epidemia que afecta de forma recurrente a todos los colores de la misma manera. La plaga mata al 10 por ciento de las margaritas; que se permite que se recuperen para a continuación ser víctimas de una nueva forma de virus. Y así continúa el ciclo a lo largo de toda la evolución del modelo.

Este experimento ilustra de qué modo la estabilidad, medida como la capacidad para regular el clima, está correlacionada con la diversidad. Las fluctuaciones de temperatura son máximas en los momentos cercanos al nacimiento y la muerte del mundo de las margaritas, cuando el número de especies es mínimo. En la flor de la vida, el efecto de las perturbaciones se resiste de forma casi completa.

Volveremos a este experimento en el capítulo 6, en relación con la capacidad actual de regulación de temperatura del biota mediante sus posibilidades de modificación de la concentración de dióxido de carbono en el aire. Este sistema específico de control climático se encuentra cerca del final de su capacidad de trabajo y se puede argumentar que las oscilaciones climáticas recientes entre edades glaciares e interglaciares son como la parte final del registro del mundo de las margaritas de la figura 3.6.

Las perturbaciones relativamente pequeñas de la oscilación orbital de la Tierra producen pequeñas variaciones en la cantidad de calor recibida por el Sol que resultan amplificadas debido a la inestabilidad de un sistema moribundo. Estos argumentos no son necesariamente aplicables a las glaciaciones ocurridas en un pasado más remoto, probablemente debidas a causas diferentes.

Los modelos del mundo de las margaritas que acabo de describir son completos pero están expresados en un lenguaje llano. Muchos científicos encuentran insatisfactoria semejante forma de expresión de una teoría y prefieren el "rigon" de las expresiones matemáticas formales. En su honor, en la figura 3.7 se muestra la esencia del modelo del mundo de las margaritas mediante un sencillo diagrama que ha elaborado mi amigo y colega Andrew Watson.

Este modelo está basado en un mundo de margaritas que sólo contienen margaritas blancas. Como son más claras de color que el suelo en el que viven tienden a incrementar el albedo de su localidad que, en consecuencia, es más fría que las áreas de superficie desnuda. Las margaritas influirán en la temperatura media del planeta desde las zonas que recubran. La relación entre el área cubierta por margaritas blancas y la temperatura superficial media del planeta se muestra mediante la curva A.

La línea de trazos paralela (A1) muestra cómo se puede desplazar la relación si hubiese algún cambio en alguna variable externa que influyese en la temperatura planetaria -por ejemplo si la estrella que calentaba el mundo de las margaritas disminuyese su aporte de energía radiante.

Las margaritas crecen mejor en un margen de temperaturas restringido. El crecimiento es máximo cerca de 20 °C y cae a 0 por debajo de 5 °C y por encima de 40 °C. La relación entre temperatura superficial del planeta y población estacionaria de margaritas sería como en la curva B, la curva parabólica.

3.7.

Regulación mediante margaritas blancas. La curva parabólica (B) describe la respuesta de las margaritas a la temperatura, y las curvas A y Al son la respuesta de la temperatura planetaria al área cubierta por las margaritas.

 

La curva A1 corresponde a un menor flujo de calor de la estrella. En ausencia de margaritas, el incremento en la temperatura planetaria (AT) sería cercano a 15 °C mientras que en presencia de éstas sólo representa alrededor de 3 °C.

Las curvas A y B relacionan la temperatura planetaria con la población del mundo de las margaritas en un estado estacionario, y el estado estacionario de todo el sistema viene indicado por el punto de intersección de estas dos curvas.

En el ejemplo puede observarse que hay dos soluciones estacionarias posibles. Resulta que las soluciones estables se encuentran en las intersecciones donde las tasas de cambio de la población y la temperatura tienen direcciones opuestas. En términos matemáticos, cuando las derivadas de las dos curvas tienen signos opuestos. La otra intersección no da lugar a una solución estable. Si el mundo de las margaritas empieza en alguna temperatura arbitraria, pero tolerable, se desplazará hacia el punto de intersección superior y se asentará allí.

¿Qué le ocurre a este estado estacionario cuando se produce algún cambio en el medio ambiente exterior?

Supongamos, por ejemplo, que la estrella se calienta tal como nuestro Sol lo hace. Si la población de margaritas se mantuviese constante de manera artificial, la temperatura planetaria acusaría simplemente el cambio en el flujo de calor de la estrella; sobrevendría un cambio de temperatura mucho más importante que si se deja crecer las margaritas hasta su nuevo estado estacionario natural, desde donde se opondrían al efecto provocado por el cambio en la radiación.

En este modelo se dan por sentados muy pocos supuestos. No es necesario aceptar que las margaritas tengan clarividencia o capacidad de previsión. Basta suponer que el crecimiento de las margaritas puede afectar a la temperatura planetaria y viceversa. Es interesante observar que el mecanismo funciona igualmente bien cualquiera que sea la dirección de los efectos. Las margaritas negras también hubieran dado lugar al mismo fenómeno. Todo lo que hace falta es que cuando están presentes el albedo sea diferente del que corresponde al suelo yermo.

La hipótesis de que el crecimiento de las margaritas está limitado a un margen estrecho de temperaturas es crucial para el funcionamiento del mecanismo, pero esta limitación dentro de un margen estrecho también se observa en toda especie viva. La curva de crecimiento con punto óptimo (B) también se observa en otras variables además de la temperatura, por ejemplo el pH (puede ser muy ácido o muy alcalino, pero es preferible la neutralidad). La mayoría de nutrientes también experimenta restricciones similares; demasiado es veneno, demasiado poco produce muerte por inanición.

La elección de una relación parabólica para la respuesta del crecimiento de las margaritas ante la temperatura es arbitraria, y hay gente que sugiere que en la vida real esta relación adquiere formas diferentes o más complejas. Para evaluar el efecto de esta observación el modelo del mundo de las margaritas se ha calculado mediante relaciones diferentes entre crecimiento y temperatura.

Todos ellos mantenían el límite de 5 a 40 °C, pero comprendían una variedad de tipos que iban desde uno rectangular (un crecimiento constante a todas las temperaturas) a uno triangular (un incremento lineal hasta un máximo y luego una pérdida lineal de la misma pendiente). También se escogieron relaciones semicirculares y rómbicas. La única limitación resultante de estos cálculos consistió en la inestabilidad de los modelos cuando aparecía una parte horizontal en las relaciones.

Volvamos atrás a la figura 3.7 e imaginemos que la curva parabólica se sustituye por una en forma de sombrero recto. La sección horizontal, o parte superior del sombrero, implicaría la existencia de un crecimiento constante a cualquier temperatura dentro del intervalo de 5 a 40 °C, en consecuencia no podría haber ninguna regulación de la temperatura. Estos modelos son parecidos a los modelos de competencia simple de la biología de poblaciones que, al ignorarse el medio ambiente, resultan notoriamente inestables.

En la medida que la velocidad de crecimiento de las margaritas varíe con la temperatura hasta un máximo y luego decrezca, se obtiene un modelo que funciona, incluso en los casos de curvatura suave en la parte superior del semicírculo.

En la Naturaleza, las relaciones que enlazan el crecimiento con alguna variable ambiental frecuentemente consisten en la combinación de un crecimiento logarítmico sobrepasado por una caída logarítmica. En los capítulos 5 y 6 estas relaciones forman parte del modelo para la regulación del oxígeno atmosférico. Cuando aumenta la concentración de oxígeno aumenta el crecimiento de los consumidores, pero el exceso de oxígeno es venenoso. Tanto demasiada abundancia como demasiada escasez de oxígeno son malas; existe una cantidad que es la deseable.

El mundo de las margaritas difiere profundamente de los intentos anteriores de modelar las especies o la Tierra. Es un modelo como los de la teoría de control, o cibernética, como también se le llama. Estos modelos consisten en sistemas autorregulados. Los ingenieros y los fisiólogos los utilizan para diseñar los pilotos automáticos de los aviones o para comprender el sistema de regulación de la respiración en los animales, y conocen qué partes del sistema deben estar estrechamente acopladas para que funcione.

En su lenguaje, el mundo de las margaritas es un sistema de bucle cerrado. Los aparatos que no están autorregulados son a menudo inestables. Los ingenieros se refieren a ellos como de «bucle abierto», los bucles son los enlaces de realimentación entre las partes del sistema. Sin embargo, el mundo de las margaritas no tiene una forma idéntica a un aparato de ingeniería. Una diferencia clave consiste en la falta de «puntos fijos» (lo cual quizá también es característico de Gaia). En los sistemas manufacturados, el usuario fija la temperatura, la velocidad, la presión o cualquier otra variable.

El valor escogido es el punto fijo y el objetivo del sistema es mantener ese valor si el medio ambiente externo cambia. El mundo de las margaritas no tiene ningún objetivo establecido como un punto fijo, sólo se sienta, como un gato, en una posición confortable y resiste los intentos de desalojarlo.

Debido al tribalismo que aísla a los seguidores de las disciplinas científicas, los biólogos, que hacen modelos del crecimiento competitivo entre especies, decidieron ignorar el medio ambiente físico y químico. Los geoquímicos, que hacen modelos de los ciclos de los elementos, y los geofísicos, que modelan el clima, decidieron ignorar la dinámica de interacción entre las especies.

En consecuencia sus modelos son incompletos, independientemente del grado de detalle que contengan. Es como si, en la figura 3.7, se considerase la biología de la relación entre población de margaritas y temperatura, pero sin referencia a la biofísica complementaria de las relaciones entre temperatura y población de margaritas. Un ingeniero o un fisiólogo identificarían que semejante planteamiento es un «bucle abierto», y en consecuencia de poco valor, excepto para estudiar casos extremos y patológicos.

También hay algo patológico en la arrogancia de algunos científicos que presumen de su conocimiento especial y de su desdén por otras disciplinas científicas. Hace sesenta años que el biólogo teórico americano Alfred Lotka, juicioso y de mente abierta, describió el modelo de competencia entre conejos y zorros en The Elements of Physical Biology [Los elementos de la biología física].

Desde entonces este modelo ha sido la inspiración de incontables investigadores en biología de poblaciones. Sin embargo ninguno hizo caso de su advertencia en la página 16:

«Debe hacerse hincapié en este hecho. Se acostumbra a discutir sobre la "evolución de las especies". A medida que avancemos veremos muchas razones por las que siempre deberemos considerar la evolución del sistema como un todo (organismos y medio ambiente). En una primera impresión puede parecer que ello dará lugar a un problema más complicado que la consideración de sólo una parte del sistema. Sin embargo, a medida que progresamos se verá que las leyes físicas que gobiernan la evolución toman con toda probabilidad una forma más sencilla cuando se refieren al sistema como un todo, en lugar de a cualquier parte del mismo».

Desde entonces, durante tres generaciones, los ecólogos teóricos han reproducido mediante modelos la evolución de los ecosistemas ignorando el medio ambiente físico, y tres generaciones de biogeoquímicos han reconstruido modelos de los ciclos de los elementos sin incluir siquiera los organismos como una parte dinámica y sensible del sistema.

En tiempos de Alfred Lotka la resolución de sistemas de ecuaciones diferenciales no lineales era una tarea amedrentadora, incluso para modelos simples como el mundo de las margaritas. En la actualidad, con la disponibilidad de los ordenadores no hay necesidad de circunscribirse a los límites estrechos de una única disciplina científica.

La visión de Lotka, según la cual el modelo sería más sencillo con todo el sistema que con cualquier parte de él, está ampliamente confirmada por las matemáticas modernas. Los sistemas de ecuaciones del tipo que describen sistemas modelo en ecología teórica y biogeoquímica son conocidos por su comportamiento caótico, tanto que ahora parecen más interesantes como objetos de juego, o para una nueva forma de ilustración gráfica.

Cuando están limitadas a una sola disciplina las matemáticas de los fenómenos naturales pueden convertirse en algo tan intrincado y complejo que a cada nuevo nivel investigado se abre un mundo nuevo de abstracción, todos ellos llenos de color. Es una pequeña maravilla que los usuarios de estas disciplinas imaginen que en sus mundos imaginarios vislumbran parte del mundo real mientras que, de hecho, están perdidos en el mundo fractal de un conjunto de Mandelbrot que reaparece siempre a cualquier nivel, desde menos a más infinito.

La ilusión es animada por matemáticos profesionales que encuentran semejanzas entre sus teorías matemáticas y las patologías del mundo real, y de numerosos científicos matemáticos actuales cuya contemplación de los demonios del hiperespacio - los «atractores extraños» del caos - es mucho más seductora que el mundo aburrido y viejo de la naturaleza.

El mundo de las margaritas proporciona una explicación plausible de cómo trabaja Gaia y de por qué predicción y previsión no son necesarias para la regulación planetaria. Sin embargo, ¿qué evidencia tenemos del mecanismo práctico? ¿Qué predicciones de la teoría de Gaia han sido confirmadas?

La primera prueba fue la expedición Viking a Marte. Aquella exploración confirmó la predicción, hecha a partir de análisis atmosféricos mediante astronomía infrarroja, de que Marte era un planeta sin vida.

Michael Whitfield, Andrew Watson y yo predijimos que la regulación a largo plazo del dióxido de carbono y del clima transcurre mediante el control biológico de la erosión de las rocas. Estas y otras pruebas se describen en los siguientes capítulos. Tiene poca importancia si la teoría de Gaia es correcta o equivocada; ya está proporcionando un punto de vista nuevo y más productivo acerca de la Tierra y de los demás planetas.

La teoría de Gaia conlleva una visión de la Tierra en la que:

1. La vida es un fenómeno a escala planetaria. A esta escala es casi inmortal y no tiene necesidad de reproducirse.
    

2. Los organismos vivos no pueden ocupar un planeta parcialmente. Sería algo tan poco duradero como un animal a medias. La regulación del medio ambiente requiere la presencia de un número suficiente de organismos vivos. Cuando la ocupación es parcial las fuerzas inevitables de la evolución física y química pronto lo convertirían en inhabitable.
    

3. Nuestra interpretación de la gran visión de Darwin ha cambiado. Gaia llama la atención sobre la falibilidad del concepto de adaptación. Ya no es suficiente decir «organismos mejor adaptados que otros tienen más probabilidad de dejar descendencia». Es necesario añadir que el crecimiento de un organismo afecta a su medio ambiente físico y químico, por tanto la evolución de las especies y la evolución de las rocas están estrechamente ligadas como un proceso único e indivisible.
    

4. La ecología teórica se ha ampliado. Tomando conjuntamente las especies y su medio ambiente físico como un solo sistema, por primera vez podemos construir modelos ecológicos que son matemáticamente estables y que sin embargo incluyen un gran número de especies en competición. En estos modelos el incremento de la diversidad entre las especies da lugar a una mejor regulación.

Este último punto supone, además, una razón poderosa que justifica nuestra cólera instintiva sobre la desconsiderada supresión de especies, una respuesta a los que dicen que es algo puramente sentimental. Ya no tenemos que justificar la preservación de la rica variedad de especies en los ecosistemas naturales, como los de las selvas tropicales húmedas, mediante débiles razones humanistas como que, por ejemplo, podrían contener plantas con principios activos capaces de curar enfermedades humanas.

La teoría de Gaia nos hace cuestionar si estos ecosistemas ofrecen mucho más que esto. Mediante su capacidad de evaporar grandes volúmenes de vapor de agua a través de la superficie de sus hojas, los árboles sirven para mantener húmedos los ecosistemas de los trópicos y el planeta frío, proporcionando una sombra de nubes blancas reflectantes.

Su sustitución por áreas de cultivo podría precipitar un desastre regional de consecuencias globales.

Regresar al Índice