by Lambros D. Callimahos

from NSA Website
 

We are not alone in the universe.

A few years ago, this notion seemed farfetched; today, the existence of extraterrestrial intelligence is taken for granted by most scientists. Sir Bernard Lovell, one of the world’s leading radio astronomers, has calculated that, even allowing for a margin of error of 5000%, there must be in our own galaxy about 100 million stars which have planets of the right chemistry, dimensions, and temperature to support organic evolution.

If we consider that our own galaxy, the Milky Way, is but one of at least a billion other galaxies similar to ours in the observable universe, the number of stars that could support some form of life is, to reach for a word, astronomical.

As to advanced (by miserable earth standards) forms of life. Dr. Frank D. Drake of the National Radio Astronomy Observatory at Green Bank, West Virginia, has stated that, putting all our knowledge together, the number of civilizations which could have arisen by now is about one billion.

The next question is, “Where is everybody?”

The nearest neighbor to our solar system is Alpha Centauri, only 4.3 light years away; but, according to Dr. Su-Shu Huang of the National Aeronautics and Space Administration (NASA), its planetary system is probably too young for the emergence of life.

Two other heavenly friends, Epsilon Eridani and Tau Ceti, about 11 light years away, are stronger contenders for harboring life. Nevertheless, if superior civilizations are abundant, the nearest would probably be at least 100 light years away; therefore, it would take 200 years for a reply to be forthcoming, a small matter of seven generations.

This should, however, make little difference to us, in view of the enormous potential gain from our contact with a superior civilization. Unless we’re terribly conceited (a very unscientific demeanor), we must assume that the “others” are far more advanced than we are. Even a 50-year gap would be tremendous; a 500 year gap staggers the imagination, and as for a 5000-year gap... (by the way, if they are as much as 50 years behind us, forget it!).

It is quite possible that “others” have satellite probes in space, retransmitting to “them” anything that sounds non-random to the probe.

But they have probably called us several thousand years ago, and are waiting for an answer; or worse yet, they have given up; or, more probably, they have reached such impressive technological advances that they have destroyed themselves.²

2 In this connection. Professor Iosif Shklovsky, Russia’s greatest radio astronomer, has the following to say in the September 1965 issue of Soviet Life:

“Profound crises lie in wait for a developing civilization and one of them may well prove fatal. We are already familiar with several such critical (situations):
(a) Self destruction as a result of a thermonuclear catastrophe or some other discovery which may have unpredictable and uncontrollable consequences
(b) Genetic danger
(c) Overproduction of information
(d) Restricted capacity of the individual’s brain which can lead to excessive specialization, with consequent dangers of degeneration
(e) A crisis precipitated by the creation of artificial intelligent beings."

Epsilon Eridani and Tau Ceti were the targets on which Dr. Drake focused his attention in the spring of 1960 in Project Ozma an attempt to detect possible intelligent signals from outer space.

The frequency selected for listening was 1420.405752 megacycles per second, or a wave length of 21 cm. This particular frequency, postulated independently by two professors on the faculty of Cornell University, Giuseppe Cocconi and Philip Morrison, happens to be the radiation frequency of atomic or free hydrogen which permeates space in great clouds; moreover, this frequency is within the range of radio frequencies able to pass through the earth’s atmosphere.

Presumably, the significance of this frequency would be known to other intelligent beings in the universe who understand radio theory. We’re still talking about radio waves as the communication medium; other possible media might be masers, lasers, or the as-yet undiscovered and unnamed “rasers.”

A technology superior to ours might even have learned how to modulate a beam of neutrinos (weightless, uncharged particles that physicists on earth find it difficult even to detect); if so, “they” may have to wait a century or two before we learn how to build a neutrino receiver.

If another civilization were trying to establish communication with us, it would first embark on attention-getting signals of such a nature that we could distinguish them from random cosmic noise; once we receive a recognizable signal, we have a good chance of understanding the message. For example, they could start with trains of signals corresponding to the natural numbers 1, 2, 3, followed perhaps by prime numbers.

They might continue with equal-length extended signals consisting of start and stop impulses, with occasional pulses in between; when these signals are aligned flush over one another, they would show a circle, the Pythagorean Theorem, or similar geometric design. These attention-getting signals would be followed by early “language lessons,” interspersed with items of technical information to help bring us up to the level of our superiors, “them.”

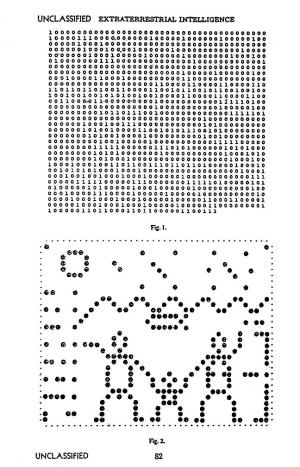
It may be assumed that the sense of sight, or an equivalent, is possessed by all higher forms of life; the problems of communication could thus be greatly simplified through the medium of a “raster” representation such as that of a television screen. After a conference held at Green Bank in 1961 to discuss the possibility of communication with other planets, one of the participants, Bernard M. Oliver, made up a hypothetical message on the raster principle.

The message, consisting of 1271 binary digits or “bits,” is shown in Fig. 1.

Since 1271 has but two prime factors, 31 and 41, we would naturally be led to write out the message in raster form, in 41 lines of 31 bits each, or in 31 lines of 41 bits each; the latter case reveals a greater non-randomness in the patterns disclosed, indicating that these are the correct dimensions. In Fig. 2 is the write-out of the message, in which the binary 1's have been replaced by a dot and the 0’s left as blank spaces.

Now for its interpretation.

There are dots at the four corners of the pictogram as reference points, marking the outlines of the rectangle. At the upper left is a representation of the sun; directly underneath in a column are dots representing 3 planets, identified by the appropriate binary coding to their left, preceded by a binary point as a marker.

The erect, two-legged beings illustrated are obviously bisexual and mammalian; one hand of the male figure points to the fourth planet where they apparently reside.

Fig. 1 and Fig. 2

At the top of the pictogram may be seen representations of hydrogen, carbon, and oxygen atoms, indicating that the chemical structure of life on their planet is similar to ours.

From the third planet there emerges a wavy line, showing that it is covered with water; the representation of a fish shows that they must have visited us and therefore have space travel. One hand of the female figure points to a six (preceded by the usual binary point), perhaps implying that there are six fingers on each hand; we could therefore assume that their number system is probably to the base 12.

At the right of the female figure may be seen a bracket, in the middle of which is eleven in binary form (preceded by a binary point!: this implies that the beings are 11 units high. A reasonable interpretation is that the unit is 21 cm., the wave length of the transmission, making them about 7½ feet tall, which should be all right for average Martians.

In 1952 the British mathematician Lancelot Hogben delivered an address before the British Interplanetary Society entitled “Astraglossa, or First Steps in Celestial Syntax.” Hogben pointed out that number is the most universal concept for establishing communication between intelligent beings; therefore, mathematics forms the basis for the first steps in extraterrestrial communication.

He then illustrated how he could transmit pulses representing integers, and distinctive signals or “radioglyphs” representing “+”, "-", “=” and so on. Morrison later carried out the basic idea a little further, using different pulse shapes to represent elementary mathematical symbols.

An entirely different approach was developed by Hans Freudenthal, Professor of Mathematics at the University of Utrecht who in 1960 published a book entitled “Lincos: Design of a Language for Cosmic Intercourse.”

“Lincos,” an acronym of “lingua cosmica,” tries to establish a communication of ideas through symbolic logic, but the general consensus of those who have taken the trouble to study his book is that his plan is too difficult.

After all, the object of the exercise is getting ideas across to another party, whose thinking processes may be entirely different from our own. In other words, what we need to develop is an “inverse cryptography,” or communication symbolism specially designed, not to hide meaning, but to be as easy as possible to comprehend. Cleverness on the part of the sender is then the important factor, not reliance on ingenuity of the recipient.

The inverse cryptographer - somehow, this term doesn’t sound quite right - must make his meaning clear to the recipient, even if the latter does not possess a cosmic equivalent of the Rosetta Stone.³

3 The Rosetta Stone is a piece of black basalt found in 1799 Dear the Rosetta mouth of the Nile, bearing a bilingual inscription (in Egyptian hieroglyphics, Egyptian demotic, and Greek) with which Jean Francois Champollion was able to solve the mystery of the Egyptian hieroglyphs.

As an illustration of how much information could be conveyed with a minimum of material, and as an example of facile inverse cryptography, let us consider a message I have devised to be typical of what we might expect of an initial communication from outer space. In Fig. 3 is shown a series of transmissions which could have come from another inhabited planet, many light years away.

The 32 arbitrary symbols are representations for the 32 different signals (combinations of beeps, or distinctive pulse shapes) heard on a frequency of 1420.4 megacycles.

The punctuation marks are not part of the message, but here represent different time lapses:

• adjacent symbols are sent with a short pause (1 unit) between them

• a space between symbols means a longer pause (2 units)

• commas, semicolons, and periods indicate pauses of 4, 8, and 16 units, respectively

Between transmissions (numbered here for reference purposes) there is a time lapse of 32 units.
 

The first transmission, (1), is obviously an enumeration of the 32 different symbols which will be used in the communications; in transmission (2) is the clear implication that A represents the integer 1, B the integer 2,.... J the integer 10.

Fig. 3                                                                                            

In the first twenty transmissions there are introduced symbols for the introductory expository treatment in teaching us their mathematics.

Among the items treated are: addition, subtraction, multiplication, and division; decimal notation and the concept of zero; inequalities and approximation; powers and roots; and definitions of π and ℮.

Transmission (21) adds nothing new to the 31 symbols recovered thus far, but it does quote one of the most beautiful concepts in pure mathematics: they are telling us that, if they can teach us such a complex notion at this early stage, we will be staggered by what they will teach us by the 200th or the 2000th transmission.

Beginning with transmission (22), words and word-cluster concepts are introduced, so that by the time we come to transmission (30), we now are understanding, in a manner of speaking, pure Venerean.

Furthermore, we can now see how we could recover the code they are using on us, and which will obviously consist of thousands upon thousands of code groups with different meanings; this is easily appreciated by anyone who takes the trouble to fathom the meaning of all 30 transmissions in the foregoing example.⁴

Even right after this first message, if we are in direct communication with that planet, we shall have questions to put to “them”: the proof of Fermat’s Last Theorem, Goldbach’s conjecture⁵ and many other unsolved problems in mathematics and the natural sciences. It will not be difficult for “them” to demonstrate their intellectual and technological superiority (first of all, don’t forget it was they who were able to call us!).

If “they” but know the seventh digit of the “fine structure constant,” they are ages ahead of us (we know only the first five for sure, suspect the sixth).

4 The solution may be found on p. 109; but eschew the premature peek.
5 With what be has learned from this example of space communication. lee the reader formulate these two questions directly for transmission to “them,” in a clear and compact form; the solutions appear on pg. 109. For the reader who is a little rusty on classic unsolved problems in mathematics. Fermat’s Last Theorem stares that DO integral values of x, y, and z can be found to satisfy the equation x² + y² = z². if π is an integer greater than 2; Goldbach’s “notorious” conjecture ("notorious” only because other mathematicians failed to make the conjecture themselves) states that every even number greater than 2 can be expressed as the sum of two primes.

This number, 137.039.... , is the ratio, among others, of the speed of light to the speed of the hydrogen electron; it may take a century to calculate this constant to 9 digits.

And after we resolve our pressing scientific questions, it might be appropriate to make discreet inquiries as to how we could live in harmony and peace with our fellow man - that is, if we aren’t eaten or otherwise ingested by the superior civilization that had the good fortune to contact us.

But as far as the cryptologist is concerned, he (and generations of his descendants who might experience the supreme thrill of their lives when we hear from “them”) must keep a level head, not get excited, and be prepared to cope with problems the like of which he has never seen - out of this world, so to speak.