Chapter 23.  Abodes of Life:  The Search Begins

"The conditions of life are indeed narrow, special, restricted; intelligent, organic life must, relatively speaking, be a rarity in the universe, but we lack the information that would enable us to affirm with any confidence that such life is only to be found upon this world of ours. Heavy as the odds are against any particular world being an inhabited one, yet when the limitless extent of space is considered, and the innumerable numbers of stars and systems of stars, it seems but reasonable to conclude that though inhabited worlds are relatively rare, the absolute number of them may be considerable."
          -- E. Walter Maunder, in Are the Planets Inhabited? (1913)⁵⁹⁹

"There are stars billions of years older than the Sun. The very oldest stars lack heavy metals; probably their planets are similarly lacking. Such very old stars are inhospitable environments for the development of technological civilizations. But some stars one or two billion years older than the Sun have no such attendant difficulties. It is surely possible that there are at least a few civilizations hundreds of millions or billions of years in our technological future."
          -- Carl Sagan, in The Cosmic Connection (1973)¹⁵

"It must not be supposed that the normal fate of intelligent races in the galaxy is to triumph."
          -- Olaf Stapledon, in Star Maker (1937)¹⁹⁴⁶

"The universe that lies about us, visible only in the privacy, the intimacy of night, is incomprehensively vast. Yet the conclusion that life exists across this vastness seems inescapable. We cannot yet be sure whether or not it lies within reach, but in any case we are a part of it all. We are not alone!"
          -- Walter Sullivan, in We Are Not Alone (1966)⁷⁰²

In previous chapters we have devoted much time to alternative alien biochemistries, physiologies, technologies, behaviors and cultural forms. Our discussion now turns from consideration of particular extraterrestrial races to the examination of the possibilities of interaction among them. When man meets alien, the human aspects of the event will be of monumental significance. Xenologists will be called upon to answer a number of very difficult questions. For instance, what is the optimum first contact procedure, both from the human standpoint and from the mutual perspective? How should we behave -- and how shall we -- when the fact of contact becomes widely known? What are the tradeoffs between physical security and the possibility of fantastic technological advancement and cultural enrichment? What is the best way to achieve understanding and community with a totally alien yet highly intelligent race of beings from another world, and what are the implications of their technology (or lack thereof)? Are there strong rationales for contacting other sentient species in the Galaxy? Why should They bother contacting us?

Before addressing these and many other fascinating issues, xenologists must consider a preliminary query: What are the chances that first contact ever will occur? In other words, is life, in general, distributed abundantly or sparsely throughout the cosmos? To answer this threshold question it is necessary to theorize in an informed manner upon the likelihood of extraterrestrial life, intelligence, and culture in our Galaxy, including its distribution and probable frequency. Much in the estimates which follow is highly speculative, but the methodology appears basically sound and yields a variety of curious results. (See especially Bond and Martin,³²²³ Bracewell,^1041,80 Freeman and Lampton,¹³⁰⁶ Hohlfeld and Terzian,²³⁸⁵ Kreifeldt,¹²⁶³ Oliver and Billingham,⁵⁷ Sagan,^1317,22 Shklovskii and Sagan,²⁰ Stull,³²⁴¹ Sullivan,⁷⁰² Tang,³⁰⁸⁷ von Hoerner,¹⁰⁵⁴ and Wertz.¹⁶¹¹)

Such studies -- sometimes called Galactic Demographics by xenologists -- are the primary concern of this brief introductory chapter.

23.1  Theoretical Galactic Demography

The late Harlow Shapley was perhaps the first astronomer ever to seriously attempt quantitatively to estimate the frequency of extraterrestrial life in the universe.⁸¹⁶ It is said that Shapley was more optimistic than his published estimates indicate, but that he deliberately chose extremely conservative numbers to forestall possible criticism from the scientific quarter. His calculation went something like this.

Suppose that only one star out of every 1000 has any planets at all. Further, let us presume that out of every 1000 worlds, only a single one is located an appropriate distance from its sun (and thus has a climate suitable for life). Then assume that out of all these well-placed planets only one in 1000 is big enough to hold an atmosphere, and that of these worlds, only one in 1000 has a chemical composition appropriate for the origin of life. Combining all of these factors, we find that only 1 star in 10¹² is graced by life. There are at least 10²¹ stars in the universe so, according to Shapley, we may expect to find about 1,000,000,000 life sites in the cosmos.

At first blush this seems like a very large number, but upon further reflection we see it is actually quite pessimistic. Since the typical habitable galaxy has about 10¹¹ stars, only one galaxy out of ten will harbor any life at all. If this calculation is correct, humanity is very much alone.

It appears that Shapley selected his step-factors of 1000 largely out of cautious conservatism without any real basis in genuine, established scientific findings. Subsequent formulations have been devised in an attempt to deal with this major failing of the Shapley calculation. The most popular alternative among xenologists today is the so-called Drake Equation¹³¹⁷ (or "Green Bank Formula"²³⁵⁸), named for its originator Frank D. Drake, a well-known American radioastronomer currently associated with the Center for Radio-physics and Space Research at Cornell University.

23.1.1  The Drake Equation

The Drake equation was developed to answer a specific and pragmatic question: How many advanced technical civilizations exist in our Galaxy, having both the interest and the ability to engage in interstellar communications of some kind? The earliest form of the Drake equation, much like the Shapley calculation, consists essentially of a string of probabilities that are multiplied together to achieve the final result.* If N is the total number of communicative extraterrestrial civilizations, then, according to Drake:

N = Nstar fp ne fl fi fc

where Nstar is the number of stars in the Milky Way Galaxy which would be suitable suns for life-bearing planets; fp is the fraction of these "good suns" actually having planetary systems; ne is the number of planets with an environment suitable for life, per solar system; fl is the fraction of suitable planets on which life finally does arise; f1 is the fraction of life-bearing worlds upon which intelligence appears; and is the fraction of planets harboring intelligent creatures who go on to develop the complex technology of interstellar communication.

What values should we assign to these variables?

At the end of Chapter 4, we concluded that about 5% of all stars in the Galaxy -- roughly ten billion suns -- should have characteristics suitable for the emergence of life. Most of these will lie in the Disk and the outer Core regions of the Milky Way. Hence we choose Nstar = 10¹⁰ "good suns."

What about fp? Astronomers now know that most stars are double or multiple.³²⁶⁰ Many "dark companions" have been confirmed, circling quite a few of the nearest stars, during the past century. There are numerous reports of possible planetary bodies (jovian-sized and larger) in orbit around a dozen or so of Sol’s stellar neighbors. In light of all the evidence, fp = 1 is probably reasonable.

How about ne? Based on the work of Dole and others, many astronomers believe that most single-star solar systems are likely to have from 7-13 major planetary bodies orbiting at various distances.^1258,2714 Further, if we use our own system as an example of the typically exotic, we see that one out of nine planets has an environment suitable at least for our kind of life (carbon aqueous). So ne = 1 is certainly a plausible estimate. (Note that the possibility of lifeforms with alternative biochemistries merely serves to increase ne.) And recent studies of the origin of life on this planet seem to suggest that abiogenesis is virtually inevitable wherever a suitable environment exists, given enough time. There is wide spread agreement that setting fl = 1 cannot be too wide of the mark.

What about the two remaining factors, fi and fc? Optimists generally assert that the development of intelligence is evolutionarily inevitable, since brains must serve the same negentropic master as the life process itself. In addition, they argue, intelligence begets society and society begets technology as population pressures mount and per capita resources dwindle. Under this view, fi = fc = 1. Other scientists are not so sanguine about the inevitability of intelligence and culture. Human intellect has risen only in the last ~10⁶ years, and culture in only perhaps ~10⁵ years. This represents a mere 0.02% and 0.002%, respectively, of the total time life has existed on Earth. Maybe we’ve just been extraordinarily lucky, and conscious intelligence normally requires much more time to emerge. Or per haps sentience usually fails to evolve at all before the local sun reaches the end of its life. And there are too many examples of technologically static and socially "arrested" cultures on Earth to ignore. Scientists who have attempted to balance these conflicting "optimistic" and "pessimistic" viewpoints generally conclude that fi = 0.1 and = fc = 0.1 are not unreasonable numbers.³²⁴¹

Multiplying all six factors together gives N = 10¹⁰ x 1 x 1 x 1 x 0.1 x 0.1 = 100,000,000 communicative technical civilizations in the Milky Way alone. Or, omitting the factor we conclude that there may be as many as one billion intelligent alien races scattered throughout the Galaxy, each separated from the next by an average distance of 34 light-years. Table 23.1 gives the estimated number of sentient extraterrestrial species expected to lie within a radius R of Earth.

 

Table 23.1 Number of Stars, "Good Suns," and Intelligent Alien Races Within Radius R of Earth, using the Early Drake Equation Formulation
Radius R	Est. Number of Stars in Disk,  Within Radius R of Earth	Est. Number of  "Good Suns"  Within Radius  R of Earth	Intelligent  Alien Races  Within Radius  R of Earth
(light-years)
10	10	(1)	(1)
20	100	5	(1)
50	1000	50	5
100	10,000	500	50
200	100,000	5000	500
500	1,000,000	50,000	5000
1000	8,000,000	400,000	40,000
2000	40,000,000	2,000,000	200,000
5000	300,000,000	15,000,000	1,500,000
10,000	900,000,000	45,000,000	4,500,000

 

This simple form of the Drake Equation is static, however. It assumes that a communicative civilization, once formed, survives indefinitely. But all species eventually become extinct; even stars and galaxies eventually must die. Xenologists who work with the Drake Equation methodology prefer to include a dynamic component which takes account of the possible destruction of civilizations. This results in the "traditional" version of the Drake Equation, as follows:

N = Rstar fp ne fl fi fc L

where Rstar is the mean rate of "good star" formation in the Galaxy (10¹⁰ stars / 10¹⁰ years = 1.0 "good suns"/year) and L is the average lifespan of a typical alien technical civilization. Plugging in numbers as before, we find that N = 1.0 x 1 x 1 x 1 x 0.1 x 0.1 x L = L/100. The mean lifetime of a civilization appears to be of critical significance in the calculation. What do we do with L? Optimists may insist that technical cultures should be able to survive for 10⁸ years. This corresponds roughly to the reign of the dinosaurs on Earth, and to the time ant society has persisted. There is no reason, argue the optimists, why humans and smart ETs could not do at least as well using the benefits of high technology. Accepting L = 10⁸ years, then N = 1,000,000 sapient cultures in the Milky Way at the present time.

Pessimists point out that human technology is highly militaristic (and even that militarism may be necessary for the evolution of intelligence and technology³²⁴¹). They note that the accumulated global destructive power today exceeds 10 tons of TNT (or its equivalent) per person. This may be viewed as a round ball of dynamite two meters in diameter hanging over the heads of every man, woman and child on Earth.²² Initiation of global destruction rests in the hands of only a few dozen people, and the world military balance becomes more precarious with each passing decade. In the opinion of the pessimists, L may be on the order of decades, not eons. (Compare Berry⁷⁷ and Viewing and Horswell³⁰⁸⁸ with Brown³²⁷² and Hoyle.²⁹⁹⁸) Choosing the "generous" value of L = 10², the number of communicative civilizations extant in the Galaxy today falls to N = 1 (that is, us).⁸⁵

The traditional Drake Equation may be written in the reduced form N = Lo L, where Lo is the mean birth rate of new technical civilizations per annum in the Milky Way. Since deaths should equal births in a stable population, L may also be interpreted as the mean death rate of advanced societies. (Mathematically, Lo = Rstar fp ne fl fi fc.) In the analysis above we found that N = L/100, or Lo = 10^-2. An optimist, however, might choose Lo = 1 society/year, in which case N = L. A pessimist, on the other hand, might select Lo = 10^-4 societies/year, which gives N = L/10,000. 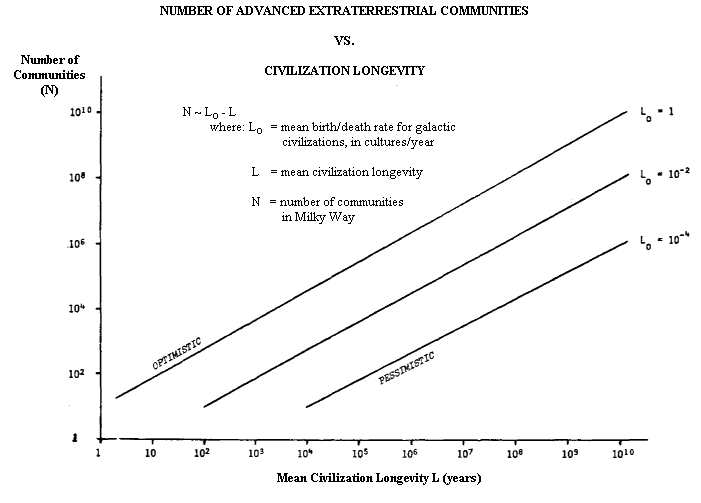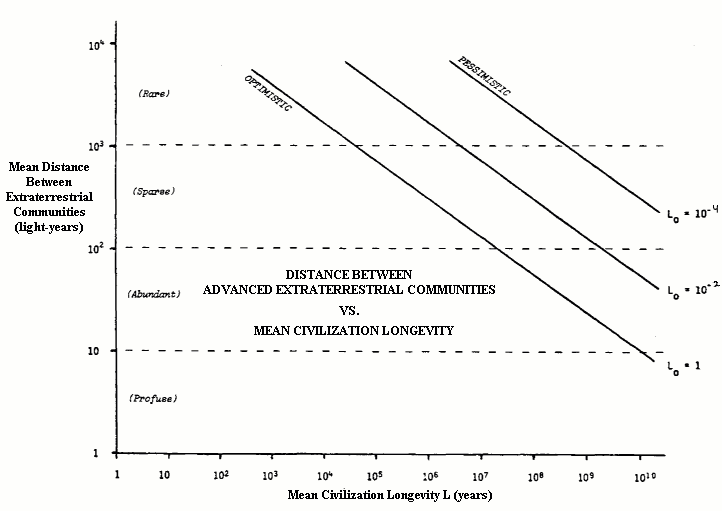(The results of choosing various ET community "turnover" rates are displayed on the graphs in Figure 23.1.) Once the xenologist has selected the cultural birth rate with which he feels most comfortable, both the number of extant technical communities and the average distance between them may be exactly determined. It is interesting to observe that only by making the most optimistic assumptions possible can we place the nearest advanced extraterrestrial civilization within 100 light-years of Earth.

 

Figure 23.1 Number of and Distance to Extraterrestrial Civlizations as a Function of Cultural Longevity

 

 

Modern xenologists have made still further improvements on the methodology of galactic demography.⁵⁷ The traditional version of the Drake Equation uses a mean value for Rstar -- the rate of formation of "good suns" in the Galaxy -- which is averaged over the estimated 10 eon lifetime of the Milky Way. Yet astrophysicists recognize that the rate of star production from interstellar gases and dust has not held constant over time. Ten eons ago, the rate was perhaps two or three orders of magnitude higher than the mean; today, it is an order or two below. By taking this fact into account xenologists are more accurately able to calculate the number of alien civilizations which coexist (or have coexisted) in the Galaxy at any time t. In mathematical terms, the number N becomes the time-function N(t).

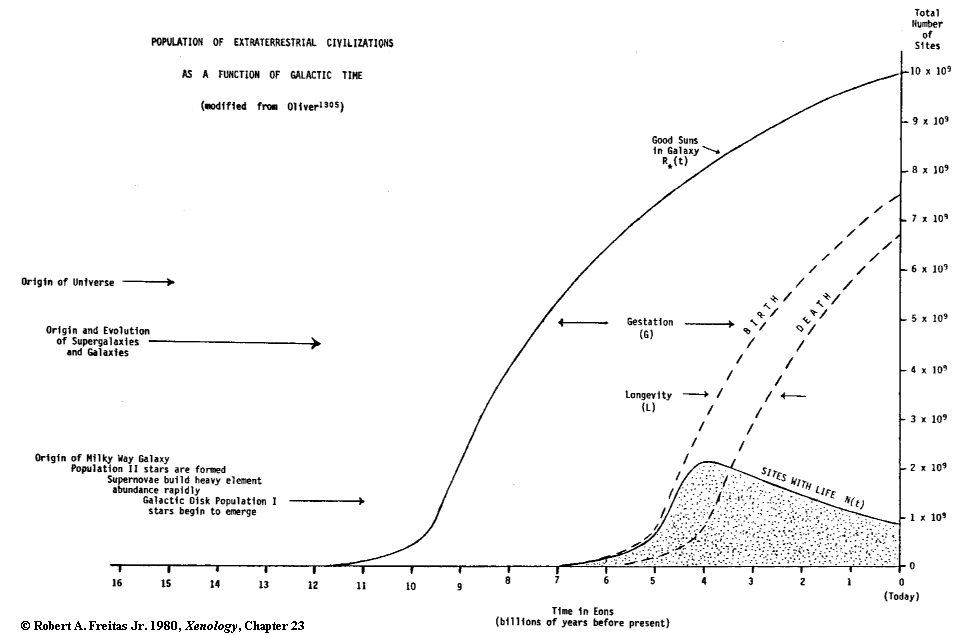
Consider the graph in Figure 23.2 below. The leftmost curve, marked R*(t), represents the total number of solar systems suitable for the emergence of life as a function of galactic time. At each of these useful sites, xenobiologists tell us, life should originate within a few hundred million years. This event is then followed by a gestation time during which life and intelligence evolve, eventually resulting in the rise of a technical culture. For reasons that will become clear presently, we choose to set fi = fc = 1 (that is, Lo = 1) for the purposes of this calculation. In other words, we optimistically assume that every "good sun" eventually spawns an advanced alien civilization.

 

Figure 23.2 Population of Extraterrestrial Civlizations as a Function of Galactic Time (modified from Oliver¹³⁰⁵)

 

Applying the Hypothesis of Mediocrity and the example of Earth, xenologists believe that a good average value for the gestation time C should be on the order of that for human culture, about 4.5 x 10⁹ years. Depending on local environmental conditions this quantity undoubtedly will vary considerably, but it seems that 4.5 eons is a reasonable mean or "expected" value.

After the gestation period has elapsed, the number of sites in the Milky Way having communicative civilizations rapidly increases, following roughly the shape of the R*(t) curve. Later, when the average lifetime L of the typical technical culture has expired, extraterrestrial civilizations begin to die off along a curve parallel to the growth. (These two curves are labeled "BIRTH" and "DEATH" on the graph.) For reasons that will become apparent, we choose a very optimistic value for L of 10⁹ years.

To obtain the Galactic population (the number of coexisting civilizations) at any given time t, galactic demographers simply subtract the death curve from the birth curve. The difference is the number of alien technical cultures which have been born but have not yet died at time t. On the graph this population curve is designated N(t).¹³⁰⁵

Perhaps the most fascinating result of this analysis is the size, shape and position of N(t). Apparently the population of coexistent technical civilizations peaked out about four billion years ago, when primeval ooze still slopped the rocky shores of ancient Earth. Humanity thus appears to be a latecomer on the cosmic stage -- the majority of Galactic history has come and gone without us.⁴⁴² Seemingly, advanced life was more common in the past than it is now.⁵⁷ While there still exist a billion sites of life extant in the Milky Way today (50% of the peak reached 4 eons ago) there are some seven billion sites of extinct alien civilizations for starfaring archaeologists of the future to pore over. In other words, about 7 of every 8 technological alien cultures that have ever existed are extinct today.

It now becomes clear why we chose such optimistic values for fi, fc, and L.

Changing these numerical assumptions to more pessimistic values does not alter the sobering conclusion that humanity may have missed most of the Galactic action. For L, we’ve already selected as optimistic a figure as common sense will permit; smaller values merely serve to decrease the galactic population overall and to shift the peak of N(t) further back in time. Choosing more conservative numbers for and in the Drake Equation has a similar effect. In fact, only by positing an unreasonably lengthy mean gestation time plus mean lifetime (G + L) greater than 12 billion years can demographers arrange for humanity to sit on the rising side of the curve representing the civilized population of the Galactic community.

 

* Skeptics have wryly asserted that the Drake Equation is nothing more than a clever way to compress a large amount of ignorance into a very small space.

 

 

23.2  Experimental Galactic Demography

Where might we expect to find alien life and civilization in nearby extrasolar space? The tables on the following three pages may serve as starting points for discussions of this speculative question.

Table 23.2 lists the 75 brightest named stars in the night sky of Earth.

Table 23.3 gives a complete inventory of all luminous stars within 20 light-years of Sol.

Table 23.4 includes a listing of all "good suns"* within 100 light-years (30 parsecs) of Sol.

*In this context, a "good sun" is a Main Sequence dwarf (Sol-like) belonging to stellar classes F5-K2. The nearest to Sol is the  a Centauri star system,³⁰⁸⁹ which recently has been discovered to be 6 eons old and significantly richer in heavy elements than our own solar system.³²²⁴

Due to unavoidably deficient data, Table 23.4 is complete only out to about 40 light-years. From 40-100 light-years, data are available only for about 25% of the "good suns" expected to lie at this range. The deficiency is almost exclusively among the class K stars (which are harder to measure at great distances) beyond 40 light-years, although many late class G suns are also missing beyond 50-60 light-years.

23.2.1  Direct Observation of Alien Planets

Assuming habitable worlds circle some or all of these distant stars, how might they be detected from Earth? There are four basic techniques, none of which has as yet provided absolutely unambiguous evidence for the existence of extrasolar planets. (See reviews by Gatewood,¹⁵⁶⁷ Huang,¹²⁷⁸ Martin^{1452,1088,1092} Matloff and Fennelly,¹⁶¹⁴ Morrison, Billingham, and Wolfe,²⁸⁶⁵ O’Leary,¹²⁴⁴ and Smith.²⁸⁶⁶) The present state of the data is summarized in Table 23.5, below.

Certainly the most fruitful approach to date has been the technique of astrometry. This requires a bit of explanation.

It will be recalled that all stars in the Milky Way orbit the galactic center much as planets circle a sun. Since each star moves with a slightly different velocity, celestial objects appear slowly to change position relative to each other over the years. Slowly, inexorably, the familiar constellations are torn asunder as the component stars move off in different directions at different speeds. For instance, the stars Sirius, Betelgeuse, Aldebaran and Arcturus have moved about the apparent diameter of the moon (Luna) since Ptolemy mapped them two millennia ago. The path traced in the sky by a wandering star is referred to as its "proper motion" by astronomers.

A lone sun traces a straight path across the sky, but a star with a retinue of invisible companion bodies should wobble slightly as it traverses the celestial vault. This is because the presence of the unseen planetary masses shifts the center of mass away from the center of the sun. The star, like its planets, actually circles this center of mass, which distant observers may observe as a tiny sinusoidal wobble with a period on the order of decades. Astrometry is a form of careful positional measurement which allows astronomers to calculate the mass and orbit of the hidden worlds based on the amplitude and frequency of wobble in the proper motion of the target star.

Imagine an hypothetical alien astronomer located 10 parsecs (33 light-years) away who wishes to demonstrate the existence of planets around Sol using astrometry. How accurate must his measurements be? Viewed from this distant observatory, our sun would subtend only 10^-3 arcsec (seconds of arc, or 1/3600 of a degree) in the sky. One-half an arcsec away from this minute yellow disk is found the giant planet Jupiter, a shining pinprick of light 10^-4 arcsec in diameter.

It is helpful to put these numbers into proper perspective in order to fully appreciate their smallness. A second of arc is considered extremely high accuracy in all normal circumstances. One arcsec is the equivalent of hitting a buzzing horsefly with a rifle bullet at a range of 2 kilometers. But Sol would subtend only 10^-3 arcsec, which is like hitting the same horsefly in New Orleans by firing a rifle in Los Angeles (more than 2000 kilometers). To use another example, consider a level tabletop. When you touch it lightly, it tilts by at least a second of arc. At the 10^-3 arcsec level the table is like the surface of a sea -- acoustic waves from people talking wash back and forth across its surface and "tilt" it by more than milliseconds of arc.

To observe Sol’s wobble due to Jupiter, our hypothetical ET astronomer would have to be able to measure variations in proper motion of about arcsec at a range of 10 parsecs. The displacement of our sun due to the presence of Earth is considerably smaller, less than 10^-6 arcsec at 10 parsecs. The state-of-the-art of astrometric precision was roughly 3 x 10^-3 arcsec for human technology in the mid-1970’s, which means that mankind is now at the threshold of the capacity to detect jovian planets circling neighboring stars.²²⁰⁰ Scientists believe that sophisticated interferometric techniques²³⁸⁷ can increase ground-based accuracy to 50 x 10^-6 arcsec, and that large spaceborne telescopes specially designed for the task can reach 10^-6 arcsec accuracies.^3092,2865 (NASA’s 2.4-meter Space Telescope has pointing stability of 0.007 arcsec.) The major difficulty with astrometry is that several cycles of the alien planet must be observed to identify and validate a discovery, which means several decades’ worth of data must be accumulated. Furthermore, the presence of more than one perturbing planetary body (Sol has 9) greatly complicates the mathematical analysis of periodicities in the wobble in proper motion of the target star.

 

Table 23.5 Possible Planetary Companions of Nearby Stars
Star	Distance	Mass of  Suspected Companion	Separation of  Star and Planet	Orbital  Period	Remarks
	(light-years)	(Jupiter = 1.0)	(AU)	(years)
Proxima Centauri	4.28	1.8	0.8	2.5	Doubtful
Barnard’s Star	5.9	1.0 and 0.4		12 and 20	Possible
Lalande 21185	8.0	10	2.8	8.0	Possible
Luytens 726-8	8.9				Needs more study
Epsilon Eridani	10.7	6	7.9	25	Needs more study
Ross 128	11.0				Needs more study
61 Cygni A	11.2	8	2.4	4.8	Possible
Luyten’s Star    (BD +55° 1668)	12.6	20		10-30	Needs more study
Kruger 60 A	12.8	9	4.1	16	Needs more study
40 Eridani A	15.8	29		3	Doubtful
BD +200 2465	16.1	10-30		10-30	Needs more study
70 Ophiuchi	16.7	10	6	17	Doubtful
BD +430 4305	16.9	10-30		20-30	Needs more study
Lalande 25372	17.4			30	Needs more study
Eta Cassiopeia A	19.2	10	6.7	18-24	Doubtful
Ross 986	19.3	13	4.0	18	Needs more study
WB 1259	34			3	Needs more study
+766° 785	60			11	Needs more study
Luyten 825-14	110			8	Needs more study
Gamma Tauri	160			>30	Needs more study
G93-48	220			6	Needs more study

 

To date, only astrometry has been exploited in the search for extrasolar worlds. But three other promising techniques have been discussed at length in scientific circles. The first of these is called the spectroscopic or "radial velocity" method.

Whereas proper motion is the apparent movement of a star across the sky, stellar "radial motion" is its velocity towards or away from us. We recall that light emitted from a moving object undergoes a Doppler shift in wavelength depending on the relative velocity of source and observer. By measuring the Doppler shift in a star’s visual spectrum, astronomers are able to determine its radial velocity. If a massive planet is present, then its orbit will cause the star’s radial velocity to oscillate much like the wobble in proper motion discussed in connection with astrometry. Rather than a positional undulation, however, the planet-hunting spectroscopist is looking for minute cyclical variations in Doppler-shifted starlight. This requires an instrument accurate to 0.08 mm visible light, able to detect variations in radial velocity on the order of 5 meters/second.¹⁵⁶⁸ To date, the most sophisticated equipment has accuracies about an order of magnitude too low, but astronomers estimate that the state-of-the-art should progress enough in a decade or two to make the spectroscopic method feasible.²⁸⁶⁵

Photometry is another promising technique. If the orbital plane of the target solar system happens to lie precisely in our line of sight, then at some point planets will cross the face of the star and partially eclipse its light. If a planet the size of Jupiter crossed in front of a star like Sol, the decrease in brightness would amount to about 1% change in total luminosity. (Passage of Earth would only cause a minute 0.008% eclipse, and so on.¹²⁵⁹) Astronomers believe that the colorimetric and photometric eclipse signature should be fairly easy to detect and to identify.¹²⁶⁶ One writer has calculated the probability of the onset or termination of an eclipse by any one of Sol's planets during a typical 6-hour observation period (a single night’s work at the telescope). For a randomly situated extraterrestrial observer, using the techniques proposed, the expected detection rate could be as high as one new solar system per year. About one star in a hundred should have a line of sight close enough to the orbital plane around Sol to allow all four of our inner planets to be detected by alien astronomers.*¹²⁵⁹ Human astronomers should prove equally lucky.

The third most promising method for spotting other worlds is direct observation. There are two main difficulties involved in this. First there is the problem of optical resolution. Seen from 10 parsecs away, Sol and Jupiter appear only 0.5 arcsec apart -- close to the limits of present-day ground-based telescopes. And planets smaller than Jupiter at the same distance, or jovian worlds farther from the star, probably could not be resolved using present instrumentation. The image of the star and planet would blur together. The second main difficulty is that the extrasolar body we seek is very faint. Shining in reflected light, the luminosity of the planet is only about 10^-8 that of the stellar primary in the visible wavelengths. Dr. Bernard Oliver of the Hewlett-Packard Corporation has estimated that sophisticated "apodization" techniques (a mask fitted over the end of the telescope to selectively reduce the brightness of the star’s diffraction pattern) could be used in a 2-meter spaceborne telescope which would just barely permit a jovian world to be resolved.²⁸⁶⁵ Indeed the Space Telescope, due to be launched by NASA in the early 1980’s, should fulfill these requirements and permit the first direct imaging of extrasolar planets.²¹⁰³ Another solution to the problem is to shift to lower frequencies where the star is relatively less bright. For example, in the infrared the luminosity differential falls from 10^-8 to 10^-4.²⁸⁶⁵ In the radio things are even better: Fennelly and Matloff have estimated that jovian planets may be detectable out to 10 parsecs using intercontinental interferometry at radio wavelengths.¹⁴⁵³

Ultimately it would be nice to be able to take detailed color photographs of terrestrial worlds across interstellar distances. Is this possible?**

Lyman J. Spitzer, Director of the Princeton University Observatory, has proposed a spaceborne occulter apparatus.³⁰⁸⁰ In this scheme, an orbiting large space telescope is pointed at the target star. A disk of black material is then placed in the instrument’s field of view in such a way that it exactly covers up the image of the star. The blazing brilliance of the primary is blotted out, permitting the detection of much fainter planetary bodies. According to Spitzer, NASA’s Space Telescope should suffice to resolve a jovian 10 parsecs away if an occulting disk 75 meters wide is placed 10,000 kilometers in front of the telescope. To spot an Earthlike extrasolar world at the same distance, a 400-meter-wide disk must be accurately positioned 250,000 kilometers ahead of the telescope. Citing the practical problems inherent in such a proposal, a few authors have advocated using Luna as an occulter.^3189,1095 To pick out jovians at 10 parsecs, a 3-meter space telescope should be placed in a near-polar 8100-km-high lunar orbit. The curved limb of the moon periodically would blot out the star light, making possible at least minute-long observations of reflected extrasolar planet light. To spot Earthlike worlds, a 7-meter space telescope should be placed in high Earth orbit, again using the distant Luna as an occulter.

Still larger systems could actually begin to resolve features on the surfaces of these faraway celestial bodies. The possibility of constructing orbital and lunar telescopes comprised of giant mirrors or huge multi-mirror arrays has been discussed in the literature.^3091,3085 According to Gerard O’Neill, the fabrication of large space structures should make interstellar imaging a snap:

It might be preferable to take advantage of a zero-gravity location by building a large number -- perhaps 10,000 -- of individual glass mirrors, each a meter in diameter, and providing each with a small locator-module, equipped with station-keeping gas jets. If the 10,000 elements were linked only by light beams, their spacing could be established by the unvarying number of wavelengths of light between each pair. That nonphysical linkage, computer-controlled, would have the further advantage that the mirrors could be programmed to separate and reform, like dancers in a slow-motion ballet. ... If located in a cross-shaped array, with individual elements spaced ten meters apart, a telescope of that kind would have the theoretical capability of resolving something as small as a changing weather system, one thousand kilometers on a side -- on the planet of a star ten light-years away.²⁷¹⁰

 

* Edward Argyle at the Dominion Radio Astrophysical Observatory in Canada has proposed a clever variation of the photometric method. Planets shine with reflected light and are located several light-minutes from the source of illumination (the star). If the emitted starlight varies, the portion reflected by the planet will be delayed in time behind the rest of the solar output. Careful photometric measurement, says Argyle, should permit the separation of these "light-echoes" from the normal starlight, thus demonstrating the presence of reflective planetary bodies and proving the existence theorem for extrasolar worlds.¹²⁸⁹

** The surface of Betelgeuse, the giant red star in the constellation Orion, has been successfully photographed using computer-enhanced "speckle interferometry" techniques.^411,3090 Surface structures are clearly visible in the photos.

Back to Contents