by Ethan Siegel
September 4, 2018

from Medium Website

Spanish version





A composite of 25 images of the Sun,

showing solar outburst/activity over a 365 day period.

Without the right amount of nuclear fusion,

 which is made possible through quantum mechanics,

none of what we recognize as life on Earth would be possible.

(NASA / SOLAR DYNAMICS OBSERVATORY

ATMOSPHERIC IMAGING ASSEMBLY / S. WIESSINGER

POST-PROCESSING BY E. SIEGEL)



Stars don't stay the same

throughout their life,

and the Sun is no exception.

Here's what's going on...

Here on Earth, the ingredients for life to survive, thrive, evolve, and sustain itself on our world have all coexisted without fail for billions of years.

In addition to all the atoms and molecules our planet possesses, our world also has the right conditions for liquid water on its surface, owing to our atmosphere and being at just the right distance from our Sun.

Yet if the Sun were either significantly cooler or hotter, that habitability would come to an abrupt end.

All the ingredients we could conceive of wouldn't change the simple fact:

without the right energy input from our Sun, life would be an impossibility.

Our Sun contains 99.8% of the Solar System's mass, but gets lighter every day. When enough time goes by, its changes will render Earth uninhabitable.

Here's how it's changing.

Artist's impression of

a young star surrounded by a protoplanetary disk.

There are many unknown properties about protoplanetary disks

around Sun-like stars, but the general picture of a dusty disk

with heavy elements distributed through

it is certainly what gave rise to our planets.

(ESO/L. CALÇADA)
 

When our Solar System first formed, a large clump of mass began gravitationally attracting more and more matter to it, forming a growing proto-star.

Surrounding it, a protoplanetary disk formed, complete with the seeds of the Solar System's future planets.

A race then ensued between two competing forces:

• gravitation, working to grow our proto-star and the planets within the disk

   

• radiation from external stars and our young, forming Sun

When radiation finally wins out, our Sun and the planets can no longer grow, and the matter that would continue to fall in gets blown away, eventually giving rise to our modern Solar System.

Asteroids in the early Solar System

were more numerous, and cratering was catastrophic.

Once the protoplanetary disk and the surrounding proto-stellar material

has evaporated away, the growth of the Solar System's overall mass ceases,

and it can only decrease from that point on.

(NASA / GSFC, BENNU'S JOURNEY - HEAVY BOMBARDMENT)
 

This marks the point where our Solar System reaches peak mass:

the most massive it will ever be.

This also marks, not so coincidentally, the point where our Sun is at its least energetic.

As long as it fuses lighter elements into heavier ones, it will never give off so little energy again. Doesn't this seem paradoxical? The Sun, from this point on, will only get less massive, while the amount of energy it emits will only go up.

If this flies in the face of what you think we know about stars, you're not alone.

After all, more massive stars do burn hotter and brighter, all things being equal.

The (modern) Morgan-Keenan spectral classification system,

with the temperature range of each star class

shown above it, in kelvin.

The overwhelming majority of stars today are M-class stars,

with only 1 known O- or B-class star within 25 parsecs.

Our Sun is a G-class star.

(WIKIMEDIA COMMONS USER LUCASVB, ADDITIONS BY E. SIEGEL)
 

There's really only a couple of factors, all in combination with one another, that determine how hot a star is.

Given that stars get their power from the nuclear fusion of lighter elements into heavier ones, we can actually enumerate what causes a star to give off energy.

The factors are:

1. The temperature at the core of the star, since higher temperatures mean more energy-per-particle, yielding a greater likelihood of a fusion event when two particles collide.

    

2. The size of the fusion region, since bigger regions where fusion can occur leads to more fusion in the same amount of time.

If we look at and compare two different stars, the more massive one tends to reach higher core temperatures and have a larger fusion region.

But if we look inside any individual star, we see something else.

The proton-proton chain is responsible

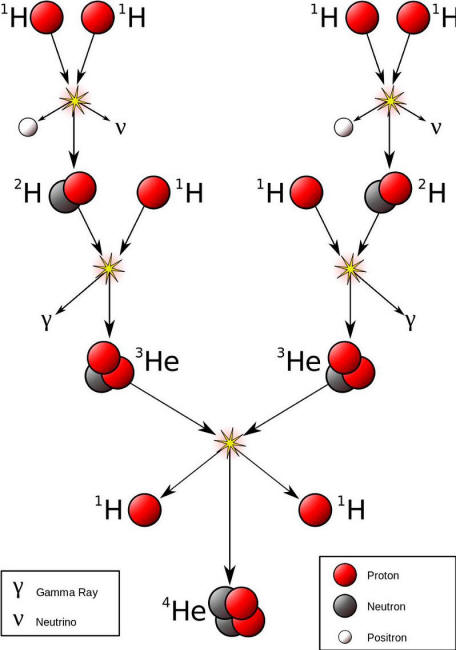
for producing the vast majority of the Sun's power.

Fusing two He-3 nuclei into He-4 is perhaps the greatest hope

for terrestrial nuclear fusion, and a clean, abundant,

controllable energy source, but all of these reaction

must occur in the Sun.

(BORB / WIKIMEDIA COMMONS)
 

The Sun, as it burns through its fuel, gains its energy by fusing hydrogen, in a chain reaction, into helium.

The proton-proton chain is how our Sun (and most stars) get their energy, since the end product (helium-4) is lighter and lower in mass than the initial reactants (4 protons).

Nuclear fusion works on the principle of mass-energy equivalence, where a small fraction of about 0.7% of the total mass of whatever gets fused is converted into energy via Einstein's E = mc².

As this occurs, the mass of the Sun slowly drops; the energy gets transported to the surface, and the “waste product” of helium sinks further down into the central region of the core.

This cutaway showcases the various regions

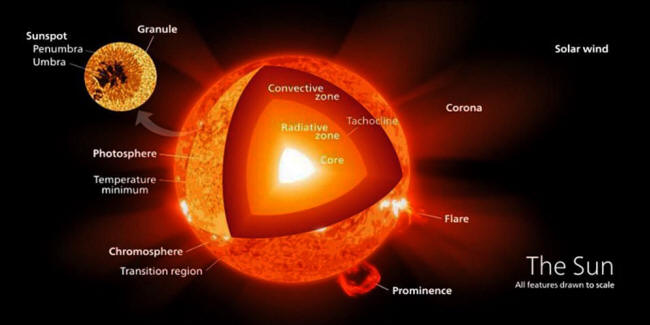
of the surface and interior of the Sun,

including the core, which is where nuclear fusion occurs.

As time goes on, the helium-containing region in the core expands,

causing the Sun's energy output to increase.

(WIKIMEDIA COMMONS USER KELVINSONG)
 

The helium at the very center cannot fuse at these temperatures, so there's less fusion-per-unit-volume occurring in the helium-rich regions.

Without fusion, there's less radiation, and the helium-rich inner part starts to contract under its own gravity. But gravitational contraction gives off energy, meaning that there's a lot of heat/thermal energy getting transported outward.

As the star ages, therefore, the interior temperatures increase, and the region where fusion can occur (at temperatures of 4 million K and up) expands outward. Overall, the rate-of-fusion and the volume where fusion occurs increases over time.

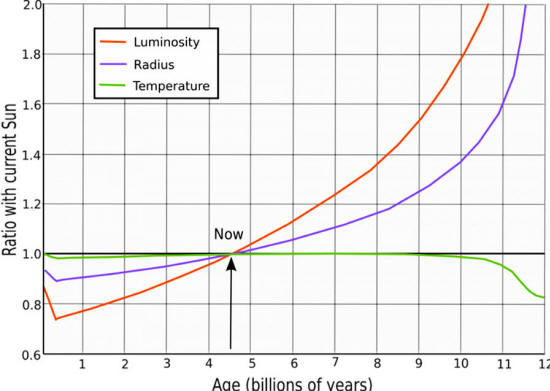
This results in the Sun  -  and all sun-like stars  -  increasing its energy output as it ages.

The evolution of the Sun's luminosity (red line) over time.

The big increase is due to the core temperature and the volume

where fusion occurs increasing as the Sun burns through its fuel.

(WIKIMEDIA COMMONS USER RJHALL, BASED ON RIBAS, IGNASI (FEBRUARY 2010)

SOLAR AND STELLAR VARIABILITY: IMPACT ON EARTH AND PLANETS,

PROCEEDINGS OF THE INTERNATIONAL ASTRONOMICAL UNION,

IAU SYMPOSIUM, VOLUME 264, PP. 3–18)
 

At the same time, the energy that gets transported to the surface not only causes the emission of light, but some of the loosely-held particles at the limb of the Sun's photosphere.

Electrons, protons, and even heavier nuclei can gain enough kinetic energy to be ejected from the Sun, creating a stream of particles known as the solar wind.

The charged particles spread throughout the Solar System and overwhelmingly leave the Solar System entirely, although a few of them will, by a chance alignment in geometry, wind up striking the atmospheres of one of the planets.

When they do, they create the effect known as an aurora, which humanity has measured and observed throughout history.

This is a false-color image

of ultraviolet Aurora Australis

 captured by NASA's IMAGE satellite

and overlaid onto NASA's

satellite-based Blue Marble image.

The Earth is shown in false color;

the aurora image,

however, is absolutely real.

(NASA)
 

Over the past 4.5 billion years, the Sun has gotten hotter, but also less massive.

The solar wind, as we measure it today, is roughly constant over time. There are the occasional flares and mass ejections, but they barely factor into the Sun's overall rate at which it loses mass.

Similarly, the Sun's fusion energy output has increased by about 20% over the course of its history, but this, too, is a small factor.

If we measure the rate of mass loss today, due to both the solar wind and to nuclear fusion, we can figure out how much lighter the Sun is getting with each second that goes by.

We can also extrapolate how much mass the Sun has lost over its entire history since it was born:

a remarkable feat...

A solar flare from our Sun,

which ejects matter out away

from our parent star and into the Solar System,

is dwarfed in terms of ‘mass loss' by nuclear fusion,

which has reduced the Sun's mass by a total of 0.03%

of its starting value: a loss equivalent to the mass of Saturn.

Until we discovered nuclear fusion, however,

we could not accurately estimate the Sun's age.

(NASA'S SOLAR DYNAMICS OBSERVATORY / GSFC)
 

The solar wind carries away about 1.6 million tonnes of mass every second, or 1.6 × 10⁹ kg/s.

That's a lot of material, for sure, and it adds up over long periods of time. Every 150 million years, the Sun loses roughly the mass of Earth due to the solar wind, or about 30 Earth masses over the entire lifetime of the Sun so far.

From fusion, however, the Sun loses even more mass than that.

The Sun's power output is a relatively consistent 4×10²⁶ W, which means it converts approximately 4 million tonnes of mass into energy each second.

From fusion, then, the Sun loses about 250% as much mass, each second, as gets carried away from the solar wind.

Over the course of its 4.5 billion year lifetime, the Sun has lost about 95 Earth masses due to fusion:

approximately the mass of Saturn.

The Sun, shown here,

generates its energy by fusing hydrogen into helium in its core,

losing small amounts of mass in the process.

Over its lifetime, it's lost approximately the mass of Saturn

by this process: about 2.5 times as much mass

as it's lost due to the solar wind.

(NASA / SOLAR DYNAMICS OBSERVATORY -SDO)
 

As time goes on, the amount of mass lost by the Sun will increase, particularly as it enters the giant phase of its life.

But even at this relatively steady rate, the growth of helium in the Sun's core means that we will heat up here on planet Earth. After about 1-to-2 billion years, the Sun will be burning hot enough that Earth's oceans will boil away entirely, making liquid water impossible on the surface of our planet.

As the Sun gets lighter and lighter, it will counter-intuitively get hotter and hotter.

Our planet has already used up approximately three-quarters of the time we have where Earth is habitable. As the Sun continues to lose mass, humanity and all life on Earth approaches its inevitable fate.

Let's make these last billion-or-so years count...